FDTD-ja FDM-algoritmit MHOF-analyysiä varten
optinen valo on luonteeltaan sähkömagneettista aaltoa, ja siten sen etenemisominaisuuksia säätelevät elektrodynamiikan lait, jotka kollektiivisesti tunnetaan Maxwellin yhtälöinä. Tiedetään, että valo-signaalien ohjaaminen MHOF: ssä fotonisilla kaistavahtirakenteilla perustuu rakentavaan interferenssivaikutukseen, joka johtuu samanlaisten ilmareikien ajoittaisesta järjestämisestä. Toisaalta, kun ilmareiät tulevat sattumanvaraisiksi kooltaan, sijainniltaan tai molemmilta, tapahtuu koko sisäisen heijastuksen ilmiö ja ytimen ja verhouksen indeksiero tarjoaa valon vangitsemisen ja siten valon ohjaamisen kuidun suuntaisesti. Vaikka monimutkaisten rakenteiden, kuten mielivaltaisten Mhofien, etenemisominaisuuksia ei pystytä helposti laskemaan analyysimenetelmillä, on olemassa keinoja ratkaista sähkömagneettisia ongelmia numeerisesti.
tässä jaksossa käsitellään kahta numeerista tekniikkaa, finite-difference time-domain (FDTD) ja finite difference method (FDM), ottaen huomioon laajennuksen holey-optisten kuitujen analyysiin mielivaltaisilla ilma-aukko-jakaumilla. Jokaisella näistä tekniikoista on tiettyjä etuja. Fdtd-menetelmää käyttäen äärellisessä avaruuden tilavuudessa olevasta jatkuvasta sähkömagneettisesta kentästä otetaan näytteet avaruuden hilan erillisistä pisteistä ja samansuuntaisista näytteenottopisteistä ajassa. Pisteissä otettuja tietoja käytetään sallittujen moodien numeerisiin laskutoimituksiin tuottamatta virheellisiä moodiratkaisuja tietyssä aaltoputkessa. Vaikka fdtd-menetelmä on tehokas menetelmä ohjattujen moodien etenemisvakioiden laskemiseksi, se ei sovellu hyvin yksittäisten moodien kenttäjakaumien arviointiin. Tämä johtuu siitä, että lähde on impulssifunktio aika-alueella, joka kattaa äärettömän spektrin, jolloin kenttäjakauman ratkaisut ovat kaikkien mahdollisten moodien superpositioita. Tämän ongelman lievittämiseksi fdtd: stä saatavilla etenemisvakioilla saadaan yksittäisiä kenttäjakaumia käyttämällä FDM: ää, joka voi nopeasti ja kätevästi tarjota yksittäisiä kenttäratkaisuja.
FDTD on saavuttanut huomattavaa suosiota viime vuosina, koska tämä menetelmä tarjoaa Maxwellin yhtälöihin perustuvia vankkoja ratkaisuja , ja siihen mahtuu helposti kompleksisesti arvostettuja materiaaliominaisuuksia. Mielivaltaista aineellista kohdetta voidaan approksimoida rakentamalla yksikkösoluja, joille kenttäkomponenttien sijainnit hävitetään halutuilla permittiivisyyden ja permeabiliteetin arvoilla. Kun kohteen geometria on määritelty numeerisella simulaatioalueella, lähdeehto mallinnetaan jossain päin aluetta. Aluksi oletetaan, että kaikki laskenta-alueen kentät ovat identtisesti nolla. Sitten, tapahtuma aalto on pakko tulla numeerinen laskenta-alueella.
käyttäen MKS: n yksikköjärjestelmää tarkastellaan ensin Maxwellin kiharayhtälöitä ilmaistuna:
missä ε on sähköinen permittiivisyysvakio F/m: ssä ja μ on magneettinen permeabiliteettivakio H/M: ssä. laajentamalla curl-lausekkeita ja rinnastamalla vastaavat komponentit muodostetaan kuuden kytketyn osittaisdifferentiaaliyhtälön järjestelmä sähkömagneettisten aaltovuorovaikutusten fdtd-analyysiä varten yleisten kolmiulotteisten kappaleiden kanssa. On huomattava, että sähkö-ja magneettikentän komponentit (Ex, Ey, Ez, Hx, Hy ja Hz) liittyvät toisiinsa. Toisin sanoen Maxwellin yhtälöt eivät suoraan tuota sähkö-ja magneettikentän arvoja, vaan suhteuttavat muutosnopeuden sähkö-ja magneettikentän arvojen välillä.
kun avaruus-ja aikajohdannaisille hyväksytään keskitetty differenssin approksimaatio toisen kertaluvun tarkkuudella, voidaan kehittää seuraavat approksimaatiot edustavina esimerkkeinä kolmiulotteisessa (3D) fdtd-formulaatiossa:
jossa I, J, K ja n ovat kokonaislukuja δx: lle, δy: lle, δz: lle ja δt: lle avaruuden ja ajan lisäyksinä .
koska Mhof: n kaltaisilla optisilla kuiduilla ei yleensä ole etenemissuunnan vaihteluja ja materiaalin ominaisuuksien vaihtelut rajoittuvat kuvassa 3 esitettyihin poikittaissuuntiin, 3D-FDTD-formulaatio voidaan yksinkertaistaa kompaktiksi kaksiulotteiseksi (2D) fdtd-algoritmiksi . Käyttämällä phasor-notaatiota aksiaalisella etenemisvakiolla (β) ensimmäisen kertaluvun osittaisderivaatat z: n suhteen korvataan arvolla-jß, koska kenttien Z-riippuvuus on muotoa exp (- jßz). Ja kaksi vierekkäistä kenttää, joita tarvitaan diskretoidun avaruuden alueen ensimmäisen kertaluvun derivaatoille, voidaan esittää niiden välisessä keskipisteessä olevalla kentällä. Näiden kahden tosiasian perusteella saadaan seuraava muotoilu esimerkiksi:
tuloksena oleva 2D-algoritmi hyödyntää tietokoneen muistin varaamisen ja käyttöajan merkittävää vähentymistä. Näin ollen tietokone-laskettaessa mielivaltaisia aaltoputkia, jotka ovat yhtenäisiä aallon etenemissuunnassa, vain aaltoputkien poikkileikkausten mallintaminen riittää.
tämän tehokkaan algoritmin ohella mielivaltaisen sähkömagneettisen kohteen 2D-avaruudessa oleva ääretön media on mallinnettava huolellisesti, koska tietokoneen muisti on laskenta-alueella rajallinen edistyneelläkin nykytekniikalla. Jotta malli alueet ulottuvat äärettömään, täydellisesti sovitettu kerros (PML) erittäin tehokas vaimentava reunaehto (ABC) on suunniteltu ulomman hilan rajan laskennan verkkotunnuksen. Ihannetapauksessa absorboiva väliaine on vain niin paksu kuin muutama ristikkokenno, erittäin absorboiva, heijastamaton kaikille impinging aalloille ja tehokas koko toiminta-aallonpituusalueella.
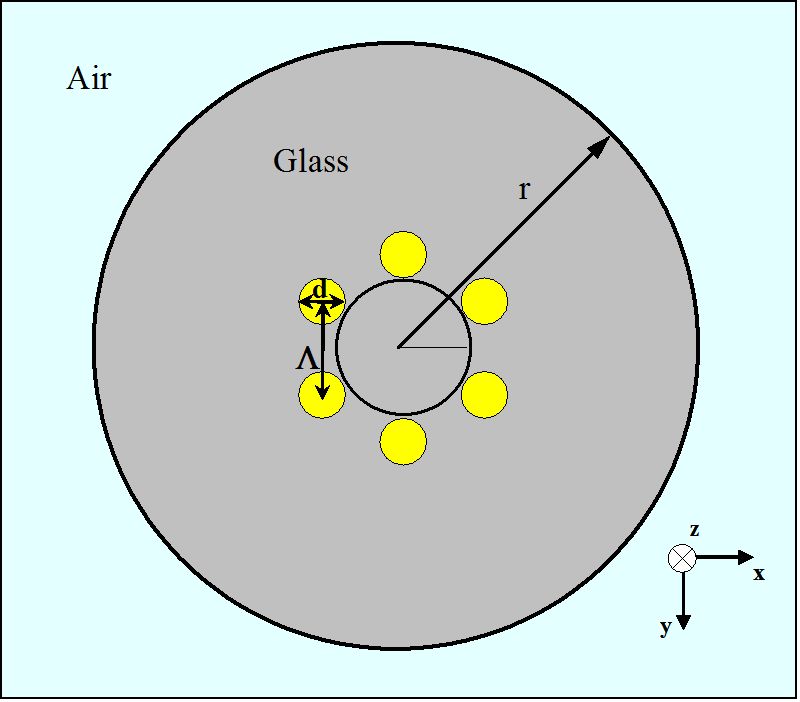
kuva 3.
kaavio MHOF-lennon poikkileikkauksesta, jossa on yksi kerros ilmareikiä kuusikulmaisessa järjestelyssä
samoin kuin fdtd-algoritmin kehitys, FDM-formula_3 voidaan johtaa kytketyistä Maxwellin yhtälöistä . Lineaaristen ja isotrooppisten väliaineiden jatkuville aalloille yhdistämällä Eqs (2) ja (3) saadaan seuraava vektoriaaltoyhtälö:
missä n on taitekerroin ja k0 on etenemisvakio vapaassa tilassa. Monia aaltoputkia, kuten optisia kuituja, voidaan pitää z-invariantteina tai paloittain Z-invariantteina rakenteina. Näillä rakenteilla taitekerroin n (x,y,z) vaihtelee hitaasti etenemissuuntaa z pitkin, mikä pätee useimpiin fotonisiin ohjautuviin laitteisiin. Käyttämällä vektori identiteetti∇×∇×=∇(∇⋅)−∇2, Eq (8)voidaan kirjoittaa muodossa
myös sillä kohtuullisella oletuksella, että Z-akselilla on mitätön aikariippuvuus, FDM-muoto kuten Eq: ssa (9) voidaan toteuttaa korvaamalla spatiaaliset derivaatat äärellisillä differenssin likiarvoilla. Tässä todetaan, että (9) poikittaiskomponentti on
, missä alaindeksi ”t” tarkoittaa poikittaiskomponentteja. Koska pituussuuntainen komponentti voidaan helposti saada soveltamalla seuraavaa nollaerojen rajoitusta (Gaussin laki) :
poikittaiskomponentit riittävät kuvaamaan sähkömagneettisen kentän täyden vektoriluonteen optisessa aaltoputkessa.
MHOFs: n ohjausominaisuuksien alustavaa tutkimusta varten Kuvassa 3 esitetty valokuitu analysoidaan tietokoneanalyysillä. Yleensä MHOF-geometriaa voidaan kuvata kahdella parametrilla, sävelkorkeuden pituudella (Λ) ja läpimitalla (d), kuten kuvassa 3 esitetään. Tässä sävelkorkeus on kahden lähimmän lieriömäisen ilmareiän keskipisteiden välinen etäisyys. Kuvan 3 MHOF: n osalta jokaisen pienen ilmareiän halkaisija on 1,4 µm, mikä muodostaa kuusikulmion, jonka Λ = 1,7 µm. Keltaisten alueiden kuutta ilmareikää ympäröivän lasiosan taitekerroin on 1,45. Holey-kuidun ulomman säteen (r) oletetaan olevan 10 µm. Myös MHOFIN ulkoalueella on ilmaa.
kun holey-kuidun poikkileikkaus on määritelty asianmukaisessa laskentakohteessa, fdtd-simulointi voidaan toteuttaa useilla määritellyillä parametreilla, kuten τ määriteltäessä Gaussin lähde, Δt stabiilille simulaatiolle, aikakomponentin näytteenottotiedon aikavaiheiden kokonaismäärä (Ntot) ja β: n kohtuulliset arvot. Jotta voidaan välttää numeeriset erot ja varmistaa fdtd-algoritmin stabiilisuus, on valittava asianmukainen Δt, joka täyttää seuraavan stabiilisuusehdon:
, jossa cM on suurin aallon vaihenopeus tietyssä numeerisessa mallissa. Yhteenveto fdtd-analyysin takana olevasta mekanismista, tietokonesimulaatio etenee seuraavasti:
-
Valitse asianmukaiset parametriarvot (τ, Δt, ntot ja β))
-
näytteenotto aika-alueen kenttäkomponentista
-
otetaan aikadatan Fourier-muunnos
-
Hae kenttäkomponentin spektritietoa
-
Pick-tilan taajuudet, jotka liittyvät β-arvoon
-
kerätään β-ja mooditaajuustietoja
-
tee kuvaaja mode index vs. aallonpituus
Kuvassa 4 esitetään ominaiskäyrät, jotka saadaan fdtd: stä lasketaan kuvassa 3 määritellyn MHOF: n kolmelle ensimmäiselle alemman kertaluvun moodille.
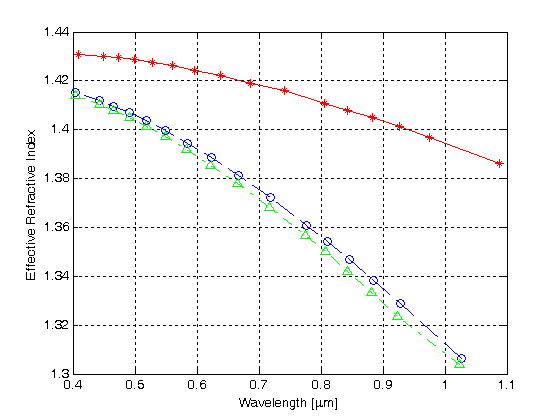
Kuva 4.
efektiivinen taitekerroin aallonpituutta vastaan kolmessa ensimmäisessä moodissa MHOF: ssa, jossa on yksi kerros ilmareikiä
punainen käyrä tähtisymboleilla piirtää normalisoidun etenemisvakion ensimmäiselle moodille ja aallonpituudelle, kun taas sininen ja vihreä käyrä osoittavat normalisoidut etenemisvakiot toiselle ja kolmannelle moodille. Tulokset osoittavat, että hmof yhdellä kuusikulmaisella ilmareikäkerroksella tukee monimodiopastusta.