Algorithmes FDTD et FDM pour l’analyse MHOF
La lumière optique est de nature électromagnétique et ses propriétés de propagation sont donc régies par les lois de l’électrodynamique qui sont collectivement connues sous le nom d’équations de Maxwell. Il est connu que le guidage de signaux lumineux dans le MHOF avec des structures de bande interdite photonique repose sur un effet d’interférence constructive dû à la disposition périodique de trous d’air identiques. D’autre part, lorsque les trous d’air deviennent aléatoires en taille, en localisation, ou les deux, le phénomène de réflexion interne totale se produit et la différence d’indice entre l’âme et la gaine assure le confinement de la lumière et donc le guidage de la lumière le long de la fibre. Bien que les caractéristiques de propagation de structures compliquées telles que les MHOFS arbitraires ne puissent pas être calculées facilement à l’aide de méthodes analytiques, il existe des moyens de résoudre numériquement les problèmes électromagnétiques.
Dans cette section, deux techniques numériques de domaine temporel à différence finie (FDTD) et de méthode à différence finie (FDM) sont abordées en vue d’une extension à l’analyse de fibres optiques trouées avec des distributions arbitraires de trous d’air. Chacune de ces techniques présente certains avantages. En utilisant la méthode FDTD, le champ électromagnétique continu dans un volume fini d’espace est échantillonné à des points distincts d’un réseau spatial et à des points d’échantillonnage également espacés dans le temps. Les données échantillonnées aux points sont utilisées pour des calculs numériques de modes autorisés, sans générer de solutions de modes parasites, dans un guide d’onde donné. Bien qu’elle soit une technique efficace pour le calcul des constantes de propagation des modes guidés, la méthode FDTD n’est pas bien adaptée à l’évaluation des distributions de champs de modes individuels. En effet, la source est une fonction impulsionnelle dans le domaine temporel couvrant un spectre infini, les solutions de distribution de champ sont donc la superposition de tous les modes possibles. Pour résoudre ce problème avec les constantes de propagation disponibles à partir de FDTD, des distributions de champs de modes individuels sont obtenues à l’aide du FDM, qui peut fournir rapidement et facilement des solutions de champs de modes individuels.
Le FDTD a acquis une popularité considérable ces dernières années, car cette méthode fournit des solutions robustes, basées sur les équations de Maxwell, et peut facilement prendre en compte les propriétés des matériaux à valeur complexe. Un objet matériel arbitraire peut être approximé en construisant des cellules unitaires pour lesquelles les positions des composants de champ sont disposées avec les valeurs de permittivité et de perméabilité souhaitées. Une fois que la géométrie de l’objet est spécifiée dans la région de simulation numérique, la condition de la source est modélisée quelque part dans la région. Initialement, on suppose que tous les champs du domaine de calcul sont identiquement nuls. Ensuite, une onde incidente est appliquée pour entrer dans la région de calcul numérique.
En utilisant le système d’unités MKS, considérons d’abord les équations de boucle de Maxwell exprimées comme:
où ε est la constante de permittivité électrique en F / m et μ est la constante de perméabilité magnétique en H / m. En élargissant les expressions de boucles et en assimilant les composantes similaires, le système de six équations aux dérivées partielles couplées est formé pour l’analyse FDTD des interactions d’ondes électromagnétiques avec des objets tridimensionnels généraux. Il est à noter que les composantes du champ électrique et du champ magnétique (Ex, Ey, Ez, Hx, Hy et Hz) sont interdépendantes. Autrement dit, les équations de Maxwell ne donnent pas directement des valeurs de champ électrique et magnétique, mais relient plutôt le taux de changement entre les valeurs de champ électrique et magnétique.
En adoptant une approximation de différence finie centrale pour les dérivées spatiales et temporelles avec une précision au second ordre, les approximations suivantes à titre d’exemples représentatifs dans une formulation FDTD tridimensionnelle (3D) peuvent être développées:
où i, j, k et n sont des entiers pour Δx, Δy, Δz et Δt, respectivement, en incréments d’espace et de temps.
Étant donné que les fibres optiques telles que les MHOFS n’ont généralement pas de variations le long de la direction de propagation et que les variations des propriétés du matériau sont limitées aux directions transversales comme le montre la figure 3, la formulation de FDTD 3D peut être simplifiée pour l’algorithme FDTD compact bidimensionnel (2D). En utilisant la notation de phaseurs avec la constante de propagation axiale (β), les dérivées partielles du premier ordre par rapport à z sont remplacées par -jß, car la dépendance z des champs est comme exp(-jßz). Et deux champs adjacents requis pour les dérivées du premier ordre dans la région d’espace discrétisé peuvent être représentés par un champ au milieu entre eux. Sur la base de ces deux faits, on obtient à titre d’exemple la formulation suivante:
L’algorithme 2D résultant tire parti d’une réduction significative de l’allocation de mémoire informatique et du temps d’exécution requis. Ainsi, pour le calcul informatique de guides d’ondes arbitraires uniformes selon la direction de propagation des ondes, seule la modélisation des sections de guides d’ondes est suffisante.
Parallèlement à cet algorithme efficace, des supports infinis dans l’espace 2D pour un objet électromagnétique arbitraire doivent être modélisés avec soin, car la mémoire de l’ordinateur est limitée dans la région de calcul, même avec une technologie actuelle avancée. Afin de modéliser des régions s’étendant à l’infini, une couche parfaitement adaptée (PML) en tant que condition aux limites absorbantes (ABC) hautement efficace est conçue à la limite de réseau externe d’un domaine de calcul. Idéalement, le milieu absorbant est seulement aussi épais que quelques cellules de réseau, très absorbant, sans réflexion à toutes les ondes impactantes et efficace sur toute la gamme des longueurs d’onde de fonctionnement.
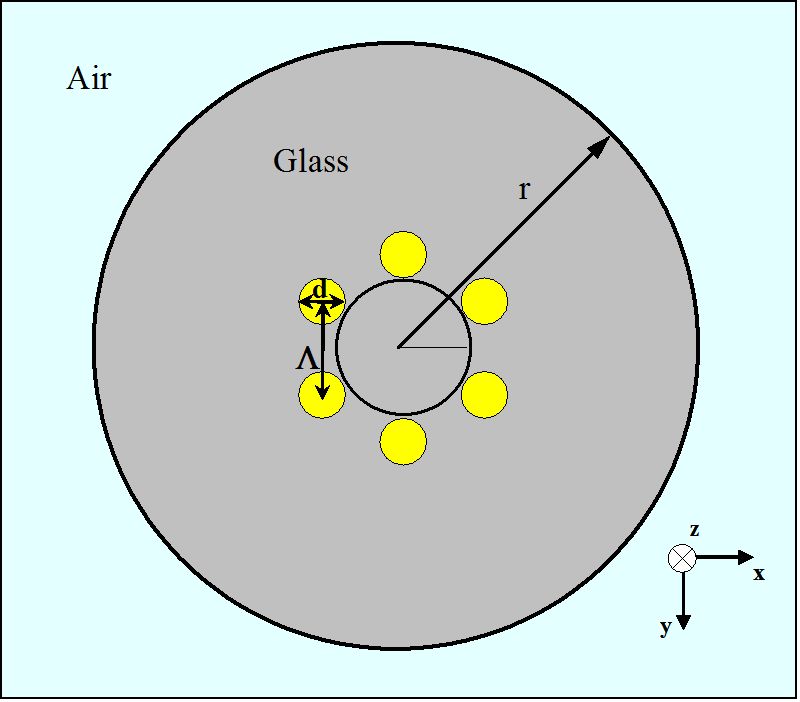
Figure 3.
Schéma d’une section transversale pour un MHOF avec une couche de trous d’air dans un agencement hexagonal
De même que le développement de l’algorithme FDTD, la formulation FDM peut être dérivée des équations de Maxwell couplées. Pour les ondes continues dans des milieux linéaires et isotropes, la combinaison des QE(2) et (3) donne l’équation vectorielle suivante:
où n est l’indice de réfraction et k0 est la constante de propagation dans l’espace libre. De nombreux dispositifs de guidage d’ondes, comme les fibres optiques, peuvent être considérés comme des structures invariantes en z ou des structures invariantes en z par morceaux. Pour ces structures, l’indice de réfraction n(x, y, z) varie lentement le long de la direction de propagation z, ce qui est valable pour la plupart des dispositifs à ondes guidées photoniques. En utilisant l’identité vectorielle de∇×∇×=∇(∇⋅)−∇2, Eq(8) peut être écrit comme
Également avec l’hypothèse raisonnable d’une dépendance temporelle négligeable le long de l’axe z, la formulation FDM comme dans Eq(9) peut être implémentée en remplaçant les dérivées spatiales par des approximations de différences finies. Ici, il est à noter que la composante transversale de (9) est
où l’indice « t » représente la transversale de composants. Étant donné que la composante longitudinale peut être facilement obtenue par application de la contrainte de divergence nulle suivante (loi de Gauss):
les composantes transversales sont suffisantes pour décrire les natures vectorielles complètes du champ électromagnétique dans un guide d’onde optique.
Pour l’étude initiale des propriétés de guidage des MHOFs, la fibre optique illustrée à la figure 3 est analysée par ordinateur. Généralement, la géométrie MHOF peut être décrite avec deux paramètres, la longueur de pas (Λ) et le diamètre (d), comme indiqué sur la figure 3. Ici, la longueur de pas est la distance entre les centres de deux trous d’air les plus proches de forme cylindrique. Pour le MHOF de la figure 3, chaque petit trou d’air a un diamètre de 1,4 µm, constituent un hexagone de Λ = 1,7 µm. La partie en verre entourant les six trous d’air des régions jaunes a un indice de réfraction de 1,45. Le rayon extérieur (r) de la fibre trouée est supposé être de 10 µm. En outre, la région extérieure du MHOF est l’air.
Une fois que la section d’une fibre creuse est définie dans un domaine de calcul approprié, la simulation FDTD peut être entreprise avec plusieurs paramètres spécifiés, tels que τ pour définir une source gaussienne, Δt pour une simulation stable, le nombre total (ntot) de pas de temps pour l’échantillonnage des données dans le domaine temporel, et des valeurs raisonnables de β. Ici, afin d’éviter la divergence numérique et d’assurer la stabilité de l’algorithme FDTD, un Δt approprié doit être sélectionné pour satisfaire la condition de stabilité suivante:
où cM est la vitesse de phase d’onde maximale dans un modèle numérique donné. Résumant le mécanisme derrière l’analyse FDTD, la simulation informatique procède par les étapes suivantes:
-
Choisissez les valeurs de paramètres appropriées (τ, Δt, ntot et β)
-
Échantillonnage de données d’un composant de champ dans le domaine temporel
-
Prendre la transformée de Fourier des données temporelles
-
Obtenir les données spectrales d’un composant de champ
-
Fréquences de mode de sélection associées à la valeur β
-
Collecter des données de fréquence β et de mode
-
Faire un graphique de l’indice de mode par rapport à la longueur d’onde
La figure 4 illustre les courbes caractéristiques, qui sont obtenues à partir du FDTD calcul, pour les trois premiers modes d’ordre inférieur du MHOF défini à la figure 3.
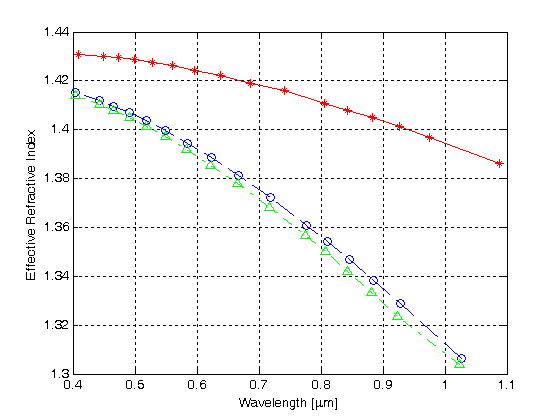
Figure 4.
Indice de réfraction effectif par rapport à la longueur d’onde pour les trois premiers modes dans un MHOF avec une couche de trous d’air
La courbe rouge avec les symboles en étoile représente la constante de propagation normalisée pour le premier mode en fonction de la longueur d’onde, tandis que les courbes bleue et verte montrent les constantes de propagation normalisées pour le deuxième et le troisième modes, respectivement. Les résultats indiquent que le HMOF avec une seule couche de gaine hexagonale à trou d’air supporte le guidage multimode.