mikä on klusterianalyysi?
klusterianalyysi on eksploratiivinen analyysi, jossa pyritään tunnistamaan aineistossa olevia rakenteita. Klusterianalyysia kutsutaan myös segmentaatioanalyysiksi tai taksonomiaanalyysiksi. Tarkemmin se pyrkii määrittelemään homogeeniset tapausryhmät, jos ryhmittely ei ole aiemmin tiedossa. Koska se on tutkiva, se ei tee eroa riippuvien ja riippumattomien muuttujien välillä. SPSS: n tarjoamilla erilaisilla klusterianalyysimenetelmillä voidaan käsitellä binäärisiä, nominaalisia, ordinaalisia ja mittakaavatietoja (intervalli tai suhde).
Klusterianalyysiä käytetään usein yhdessä muiden analyysien (kuten diskriminanttianalyysin) kanssa. Tutkijan on kyettävä tulkitsemaan klusterianalyysiä sen perusteella, miten hän ymmärtää aineistoa, jotta voidaan selvittää, ovatko analyysin tuottamat tulokset todella merkityksellisiä.
tyypillisiä tutkimuskysymyksiä klusterianalyysin vastaukset ovat seuraavat:
- lääketiede – mitkä ovat diagnostiset klusterit? Vastatakseen tähän kysymykseen tutkija laatisi diagnostisen kyselylomakkeen, joka sisältää mahdolliset oireet (esimerkiksi psykologiassa, ahdistuksessa, masennuksessa jne.). Klusterianalyysissä voidaan sitten tunnistaa potilasryhmiä, joilla on samanlaisia oireita.
- markkinointi – mitkä ovat asiakassegmentit? Vastatakseen tähän kysymykseen markkinatutkija voi tehdä kyselyn, joka kattaa asiakkaiden tarpeet, asenteet, väestötiedot ja käyttäytymisen. Tämän jälkeen tutkija voi klusterianalyysin avulla tunnistaa homogeeniset asiakasryhmät, joilla on samanlaiset tarpeet ja asenteet.
- koulutus-mitkä ovat erityishuomiota vaativat opiskelijaryhmät? Tutkijat voivat mitata psykologisia, soveltuvuusominaisuuksia ja suoritusominaisuuksia. Klusterianalyysi voi sitten tunnistaa, mitä homogeenisia ryhmiä on opiskelijoiden keskuudessa (esimerkiksi hyvin menestyneet kaikissa aineissa tai opiskelijat, jotka menestyvät tietyissä aineissa mutta epäonnistuvat toisissa).
- biologia-mikä on lajien taksonomia? Tutkijat voivat kerätä tietoa eri kasveista ja huomata niiden fenotyyppien eri attribuutteja. Klusterianalyysillä voidaan ryhmitellä nämä havainnot ryppäiksi ja auttaa rakentamaan samankaltaisten kasvien ryhmistä ja alaryhmistä taksonomia.
muita menetelmiä, joita kannattaa kokeilla samankaltaisten havaintoryhmien tunnistamiseksi, ovat Q-analyysi, moniulotteinen skaalaus (MDS) ja piilevä luokka-analyysi.
klusterianalyysi SPSS: ssä
tutkimuskysymyksemme tähän esimerkkiklusterianalyysiin on seuraava:
mitkä homogeeniset opiskelijaryhmät syntyvät standardoitujen matematiikan, lukemisen ja kirjoittamisen testipisteiden perusteella?
SPSS: n Klusterianalyysit löytyvät kohdasta Analyze/Classify…. SPSS tarjoaa klusterianalyysiin kolme menetelmää: K-tarkoittaa klusteria, hierarkkista klusteria ja kaksivaiheista klusteria.
K-means cluster on menetelmä suurten tietojoukkojen nopeaan klusterointiin. Tutkija määrittelee klustereiden määrän etukäteen. Tämä on hyödyllistä testata eri malleja, joilla on eri oletettu määrä klustereita.
hierarkkinen klusteri on yleisin menetelmä. Se luo sarjan malleja klusteriratkaisuilla 1: stä (kaikki tapaukset yhdessä klusterissa) n: ään (jokainen tapaus on yksittäinen klusteri). Hierarkkinen klusteri toimii myös muuttujien kanssa toisin kuin tapaukset; se voi klusteroida muuttujia yhteen tavalla, joka muistuttaa jonkin verran tekijäanalyysiä. Lisäksi hierarkkisessa klusterianalyysissä voidaan käsitellä nominaali -, ordinaali-ja mittakaavatietoja, mutta ei ole suositeltavaa sekoittaa eri mittaustasoja.
kaksivaiheinen klusterianalyysi tunnistaa ryhmittymät ajamalla ensin esiklusteroinnin ja sitten hierarkkiset menetelmät. Koska se käyttää nopeaa klusterialgoritmia etukäteen, se pystyy käsittelemään suuria datajoukkoja, joiden laskeminen hierarkkisilla klusterimenetelmillä kestäisi kauan. Tässä suhteessa se on yhdistelmä kahdesta edellisestä lähestymistavasta. Kaksivaiheinen ryhmittely voi käsitellä mittakaava-ja ordinaalidataa samassa mallissa, ja se valitsee automaattisesti klustereiden määrän.
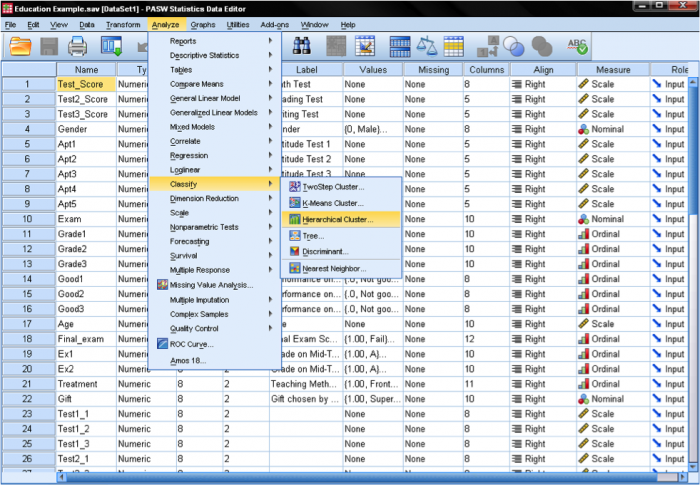
hierarkkisessa klusterianalyysissä noudatetaan kolmea perusvaihetta: 1) lasketaan etäisyydet, 2) yhdistetään klusterit ja 3) valitaan ratkaisu valitsemalla oikea määrä klustereita.
ensin on valittava muuttujat, joihin klusterimme perustuvat. Valintaikkunassa lisäämme matematiikka -, lukeminen-ja kirjoitustestit muuttujien luetteloon. Koska haluamme klusterin tapauksia jätämme loput rasti merkit oletuksena.
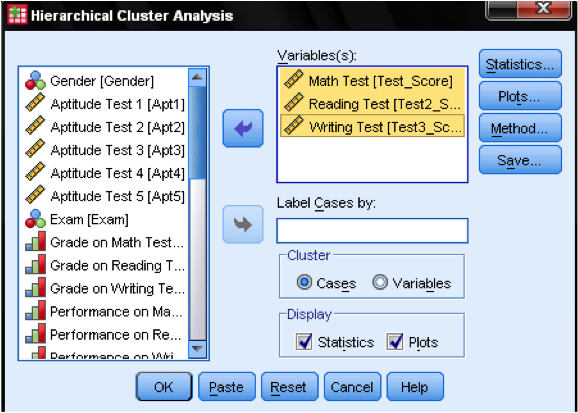
valintaikkunassa tilastot … voimme määrittää, haluammeko tulostaa läheisyysmatriisin (nämä ovat analyysin ensimmäisessä vaiheessa lasketut etäisyydet) ja havaintojen tapausten ennustetun klusterijäsenyyden. Jälleen, jätämme kaikki asetukset oletuksena.

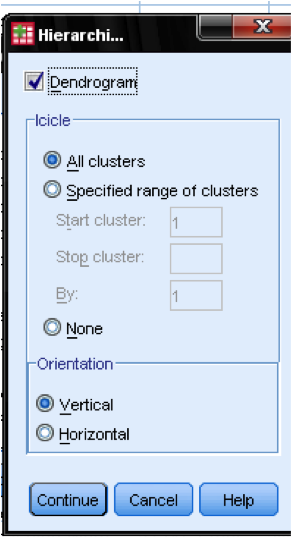
valintaikkunassa tontit … meidän pitäisi lisätä Dendrogram. Dendrogram näyttää graafisesti, miten klusterit yhdistyvät, ja sen avulla voimme tunnistaa, mikä on sopiva määrä klustereita.
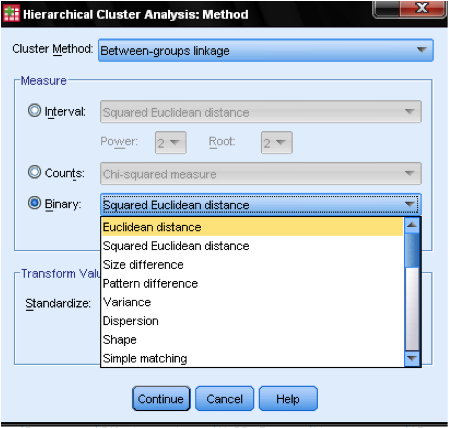
valintaikkunan menetelmän avulla voimme määrittää etäisyyden mittauksen ja ryhmittelymenetelmän. Ensinnäkin meidän on määriteltävä oikea etäisyyden mitta. SPSS tarjoaa kolme suurta lohkoa etäisyysmittareita intervallille (asteikko), laskuille (ordinaalinen) ja binääriselle (nimellinen) datalle.
intervallitiedoissa yleisin on neliömäinen Euklidian Etäisyys. Se perustuu kahden havainnon väliseen Euklidian etäisyyteen, joka on neliöjuuri neliömäisten etäisyyksien summasta. Koska Euklidian etäisyys on neliö, se lisää suurten etäisyyksien merkitystä, mutta heikentää pienten etäisyyksien merkitystä.

jos meillä on ordinaaliset tiedot (luvut), voimme valita Chi-neliön tai standardoidun Chi-neliön, jota kutsutaan Phi-neliöksi. Binääridatassa käytetään yleisesti neliömäistä Euklidista etäisyyttä.

esimerkissämme valitsemme intervallin ja neliömäisen euklidisen etäisyyden.
seuraavaksi on valittava Klusterimenetelmä. Tyypillisesti valinnat ovat ryhmien välinen yhteys (klusterien välinen etäisyys on kaikkien tietopisteiden keskimääräinen etäisyys näissä klustereissa), lähin naapuri (yksittäinen yhteys: klusterien välinen etäisyys on pienin etäisyys kahden tietopisteen välillä), kaukaisin naapuri (täydellinen yhteys: etäisyys on suurin etäisyys kahden tietopisteen välillä) ja Wardin menetelmä (etäisyys on kaikkien klustereiden etäisyys näytteen suureen keskiarvoon). Yksittäinen yhteys toimii parhaiten pitkissä klustereissa, kun taas täydellinen linkitys toimii parhaiten tiheissä klustereissa. Ryhmien välinen yhteys toimii molempien klusterityyppien kanssa. On suositeltavaa käyttää yhden linkin ensimmäinen. Vaikka yksittäinen yhteys yleensä luo klusteriketjuja, se auttaa tunnistamaan poikkeavia tekijöitä. Poistettuamme nämä poikkeamat voimme siirtyä Wardin menetelmään. Wardin menetelmä käyttää F-arvoa (kuten anovassa) maksimoidakseen klustereiden välisten erojen merkityksen.
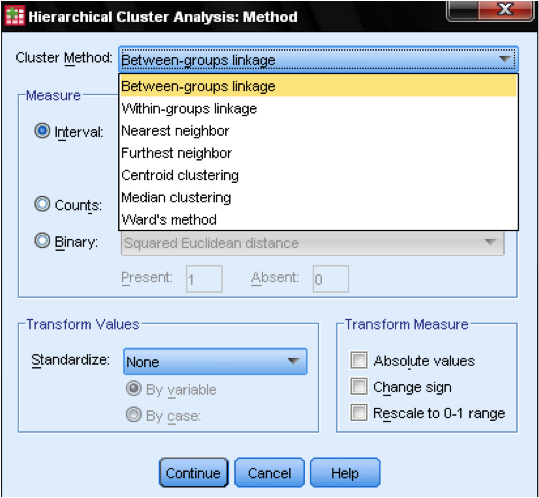
viimeinen näkökohta on standardointi. Jos muuttujilla on eri asteikot ja keinot, voimme ehkä standardoida joko Z-pisteisiin tai asteikon keskittämiseen. Voimme myös muuttaa arvot itseisarvoiksi, jos meillä on tietokokonaisuus, jossa se voisi olla tarkoituksenmukaista.