Algoritmos FDTD y FDM para el análisis MHOF
La luz óptica es onda electromagnética en la naturaleza, y por lo tanto sus propiedades de propagación se rigen por las leyes de la electrodinámica que se conocen colectivamente como ecuaciones de Maxwell. Se sabe que la guía de señales de luz en el MHOF con estructuras fotónicas de banda ancha se basa en el efecto de interferencia constructiva debido a la disposición periódica de orificios de aire idénticos. Por otro lado, cuando los orificios de aire se vuelven aleatorios en tamaño, ubicación o ambos, se produce el fenómeno de reflexión interna total y la diferencia de índice entre el núcleo y el revestimiento proporciona confinamiento de la luz y, por lo tanto, guía de la luz a lo largo de la fibra. Aunque las características de propagación de estructuras complicadas como MHOFs arbitrarios no se pueden calcular fácilmente utilizando métodos analíticos, hay formas de resolver problemas electromagnéticos numéricamente.
En esta sección, se abordan dos técnicas numéricas de dominio temporal de diferencia finita (FDTD) y método de diferencia finita (FDM) considerando la extensión al análisis de fibras ópticas perforadas con distribuciones arbitrarias de orificios de aire. Cada una de estas técnicas tiene ciertas ventajas. Usando el método FDTD, el campo electromagnético continuo en un volumen finito de espacio se muestrea en puntos distintos en una red espacial y en puntos de muestreo igualmente espaciados en el tiempo. Los datos muestreados en los puntos se utilizan para cálculos numéricos de modos permitidos, sin generar soluciones de modo espurio, en una guía de onda dada. A pesar de ser una técnica eficaz para el cálculo de constantes de propagación de modos guiados, el método FDTD no es adecuado para la evaluación de distribuciones de campos de modo individuales. Esto se debe a que la fuente es una función de impulso en el dominio del tiempo que cubre un espectro infinito, por lo que las soluciones de distribución de campo son la superposición de todos los modos posibles. Para aliviar este problema con las constantes de propagación disponibles en FDTD, las distribuciones de campo de modo individual se obtienen utilizando FDM, que puede proporcionar soluciones de campo de modo individual de forma rápida y conveniente.
El FDTD ha ganado considerable popularidad en los últimos años, porque este método proporciona soluciones robustas, basadas en las ecuaciones de Maxwell , y puede adaptarse fácilmente a propiedades de materiales de valor complejo. Un objeto material arbitrario se puede aproximar mediante la construcción de celdas unitarias para las que se disponen las posiciones de los componentes de campo con los valores deseados de permitividad y permeabilidad. Una vez que se especifica la geometría del objeto en la región de simulación numérica, la condición de origen se modela en algún lugar de la región. Inicialmente, se asume que todos los campos dentro del dominio de cálculo son idénticos a cero. Luego, se impone una onda de incidente para ingresar a la región de cálculo numérico.
Usando el sistema de unidades MKS, consideremos primero las ecuaciones de curvatura de Maxwell expresadas como:
donde ε es la constante de permeabilidad eléctrica en F / m y μ es la constante de permeabilidad magnética en H / m. Expandiendo las expresiones de rizo y equiparando los componentes similares, se forma el sistema de seis ecuaciones diferenciales parciales acopladas para el análisis FDTD de interacciones de ondas electromagnéticas con objetos tridimensionales generales. Cabe señalar que los componentes del campo eléctrico y magnético (Ex, Ey, Ez, Hx, Hy y Hz) están interrelacionados. Es decir, las ecuaciones de Maxwell no producen directamente valores de campo eléctrico y magnético, sino que relacionan la tasa de cambio entre los valores de campo eléctrico y magnético.
Adoptando una aproximación de diferencia finita central para derivadas de espacio y tiempo con precisión de segundo orden, se pueden desarrollar las siguientes aproximaciones como ejemplos representativos en una formulación FDTD tridimensional (3D) :
donde i, j, k, y n son enteros para Δx, Δy, Δz, y T, respectivamente, como el espacio y los incrementos de tiempo .
Dado que las fibras ópticas como los MHOF generalmente no tienen variaciones a lo largo de la dirección de propagación y las variaciones de las propiedades del material se limitan a las direcciones transversales como se muestra en la Figura 3, la formulación FDTD 3D se puede simplificar al algoritmo FDTD compacto bidimensional (2D). Mediante el uso de notación fasórica con la constante de propagación axial (β), las derivadas parciales de primer orden con respecto a z se sustituyen por-jß, porque la dependencia z de los campos es como exp (- jßz). Y dos campos adyacentes requeridos para las derivadas de primer orden en la región espacial discretizada pueden ser representados por un campo en el punto medio entre ellos. Sobre la base de estos dos hechos, se obtiene la siguiente formulación como ejemplo:
El algoritmo 2D resultante aprovecha la reducción significativa en la asignación de memoria de computadora requerida y el tiempo de ejecución. Por lo tanto, para el cálculo por computadora de guías de onda arbitrarias que son uniformes a lo largo de la dirección de propagación de la onda, solo es suficiente el modelado de las secciones transversales de las guías de onda.
Junto con este algoritmo eficiente, los medios infinitos en el espacio 2D para un objeto electromagnético arbitrario deben modelarse cuidadosamente, porque la memoria de la computadora está limitada en la región de cálculo incluso con tecnología actual avanzada. Para modelar regiones que se extienden hasta el infinito, se diseña una capa perfectamente emparejada (PML) como una condición de límite absorbente altamente efectiva (ABC) en el límite de red exterior de un dominio de cálculo. Idealmente, el medio absorbente es tan grueso como unas pocas celdas de celosía, altamente absorbente, sin reflejos para todas las ondas de impacto y efectivo en todo el rango de longitudes de onda operativas.
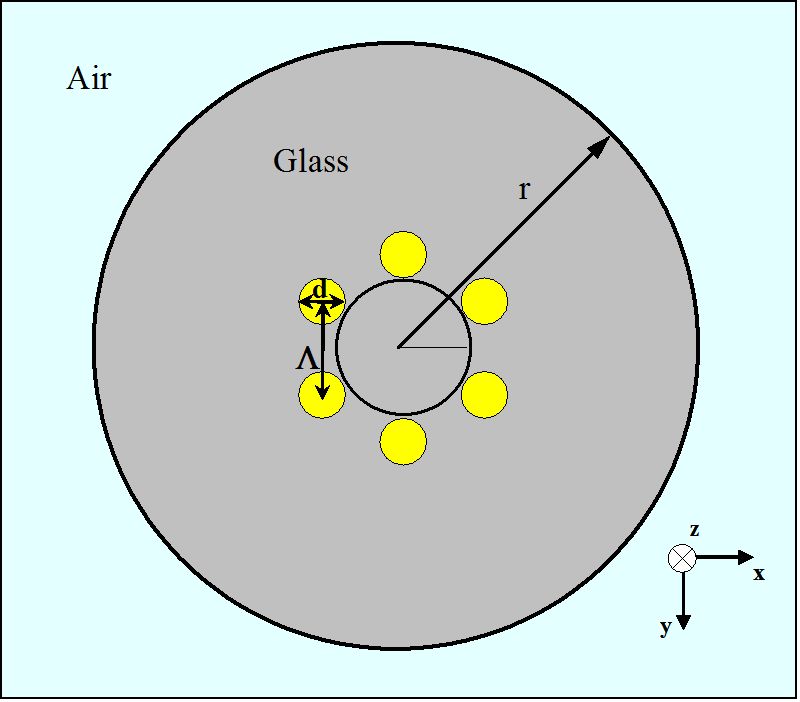
Gráfico 3
Esquema de una sección transversal para un MHOF con una capa de orificios de aire en una disposición hexagonal
De manera similar al desarrollo del algoritmo FDTD, la formulación FDM puede derivarse de las ecuaciones de Maxwell acopladas . Para ondas continuas en medios lineales e isotrópicos, la combinación de ecualizadores (2) y (3) da como resultado la siguiente ecuación de onda vectorial:
donde n es el índice de refracción y k0 es la constante de propagación en espacio libre. Muchos dispositivos de guía de ondas, como las fibras ópticas, se pueden ver como estructuras invariantes en z, o por partes invariantes en z. Para esas estructuras,el índice de refracción n(x,y, z) varía lentamente a lo largo de la dirección de propagación z, que es válida para la mayoría de los dispositivos de ondas guiadas fotónicas. Mediante el uso de la identidad vectorial de∇×∇×=∇(∇⋅)−∇2, Eq (8) se puede escribir como
También con la suposición razonable de una dependencia temporal insignificante a lo largo del eje z, la formulación FDM como en Eq (9) se puede implementar reemplazando derivadas espaciales con aproximaciones de diferencias finitas. Aquí, se observa que el componente transversal de (9)es
donde el subíndice «t» representa los componentes transversales. Dado que el componente longitudinal se puede obtener fácilmente mediante la aplicación de la siguiente restricción de divergencia cero (ley de Gauss) :
los componentes transversales son suficientes para describir la naturaleza vectorial completa del campo electromagnético en una guía de onda óptica.
Para la investigación inicial de las propiedades de guía de los MHOFs, la fibra óptica que se muestra en la Figura 3 se analiza por computadora. Generalmente, la geometría MHOF se puede describir con dos parámetros, longitud de paso (Λ) y diámetro (d), como se indica en la Figura 3. Aquí, la longitud de paso es la distancia entre los centros de dos orificios de aire más cercanos con la forma cilíndrica. Para el MHOF de la figura 3, cada pequeño orificio de aire tiene un diámetro de 1,4 µm, constituyendo un hexágono con Λ = 1,7 µm. La porción de vidrio que rodea los seis orificios de aire de las regiones amarillas tiene un índice de refracción de 1,45. Se supone que el radio exterior (r) de la fibra perforada es de 10 µm. Además, la región exterior del MHOF es aire.
Una vez definida la sección transversal de una fibra perforada en un dominio de cálculo adecuado, la simulación FDTD se puede realizar con varios parámetros especificados, como τ para definir una fuente gaussiana, Δt para simulación estable, el número total (ntot) de pasos de tiempo para datos de muestreo en el dominio de tiempo y valores razonables de β. Aquí, para evitar la divergencia numérica y garantizar la estabilidad del algoritmo FDTD, se debe seleccionar un Δt apropiado para satisfacer la siguiente condición de estabilidad:
donde cM es la velocidad máxima de fase de onda dentro de un modelo numérico dado. Resumiendo el mecanismo detrás del análisis FDTD, la simulación por computadora procede de los siguientes pasos:
-
Elija los valores de parámetros adecuados (τ, Δt, ntot y β)
-
Muestreo de datos de un componente de campo en el dominio de tiempo
-
Tome la transformada de Fourier de los datos de tiempo
-
Obtener datos espectrales de un componente de campo
-
Frecuencias de modo de selección asociadas con el valor β
-
Recopilar datos de frecuencia de modo y β
-
Hacer una gráfica de índice de modo versus longitud de onda
La Figura 4 ilustra las curvas características, que se obtienen de la FDTD cálculo, para los tres primeros modos de orden inferior del MHOF definido en la Figura 3.
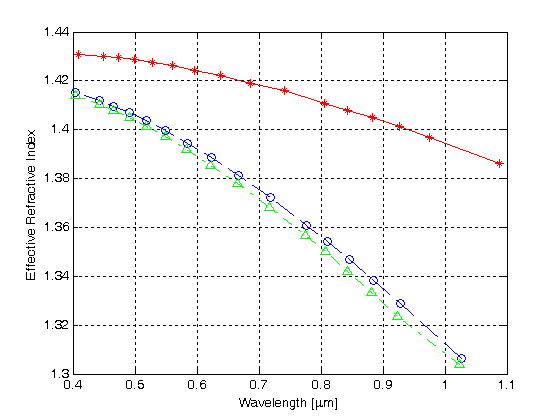
Gráfico 4
Índice de refracción efectivo frente a longitud de onda para los tres primeros modos en un MHOF con una capa de orificios de aire
La curva roja con los símbolos de estrella representa la constante de propagación normalizada para el primer modo frente a la longitud de onda, mientras que las curvas azul y verde muestran las constantes de propagación normalizadas para el segundo y el tercer modo, respectivamente. Los resultados indican que el HMOF con una sola capa de revestimiento de orificio de aire hexagonal soporta la guía multimodo.