omtrek AND HOW TO FIND
er zijn een paar manieren om de omtrek van pijp en ronde buis te vinden. Het kennen van de omtrek is de sleutel tot het bouwen van nauwkeurige sjablonen voor gebruik met pijp. Hoe nauwkeuriger uw cijfers zijn bij het ontwikkelen van deze template, hoe beter u zult hebben. Zoals met alles, de praktijk en ervaring in het bouwen van sjablonen zal ook de nauwkeurigheid te verhogen.
de meest gebruikte methode voor het berekenen van de omtrek is het gebruik van de formule Pi x diameter. 6 “od ronde buis heeft een omtrek van 18.85”. 6 “x Pi = 18,85”. Als het gaat om het werken met pijp, moet u zich ervan bewust zijn dat pijp is nominaal meten. Dit betekent dat 6 “pijp is niet 6” OD. Gelukkig volgen alle pijpfabrikanten een standaard en zijn er talloze tabellen en grafieken die alle pijpgroottes en zelfs de omtrek van alle maten weergeven! Raadpleeg index om deze tabellen, grafieken en andere informatie te vinden.
in de volgende secties zullen we beginnen met het ontwikkelen van sjablonen voor gebruik met pipe. Ongeacht de complexiteit van de template zijn er verschillende sleutelbegrippen die met elk van hen worden gebruikt, waaronder het bepalen van de omtrek. We zullen deze concepten slechts één keer in detail introduceren, als u hulp nodig heeft, verwijzen we u naar een eerdere paragrafen.
we zullen het hebben over het verdelen van de omtrek van de pijp in verschillende gelijke delen die zullen helpen bij het ontwikkelen van de template. We zullen naar deze lijnen verwijzen als elementlijnen. Hoe meer elementlijnen je hebt, hoe nauwkeuriger de pasvorm.
zoals eerder werd gezegd, zijn er vele manieren waarop ambachtslieden oplossingen hebben gevonden voor complexe problemen, dit is boek biedt een van die.
hieronder hebben we een 4 ” pijp. Door te verwijzen naar de grafiek kunnen we zien dat de OD van die pijp 4.50″is. Ook op de horoscoop zien we dat het een totale omtrek heeft van 14,125″. Voor dit boek zullen we alle omtrekken verdelen in 16 gelijke ruimten waarin de elementlijnen zullen worden. De handige grafiek in de achterkant toont ons ook de afstand voor het verdelen van de omtrek in 16 delen, evenals 12, 8, 6, 4 en 2. Onthoud, hoe meer elementlijnen je hebt, hoe nauwkeuriger je template zal zijn. Als we de grafiek niet hadden, zou je de totale omtrek moeten delen door het aantal benodigde spaties. Sommige afronding zal nodig zijn bij het doen van dit, maar je moet je ervan bewust zijn dat het zijn uit 1/16″, 16 keer zal uiteindelijk worden uitgeschakeld door een volledige 1″.
als u 14,125 door 16 deelt, komt u op .883. De kaart in de achterste staat .875. .875, of 7/8 ” is veel gemakkelijker om te werken met een meetlint dan .883. Het verschil is ongeveer 1/132 per regel, Dit is aanvaardbaar.
om te beginnen zullen we een zijaanzicht tekenen dat de hoogte van ons pijpgedeelte laat zien. Vervolgens moeten we onze stretch-out tekenen. We weten dat de omtrek 14.125 is. We kunnen een verticale naast zijaanzicht een pijp te tekenen en vervolgens uit te breiden de horizontale lijnen (weergegeven in het rood) die de bovenste en onderste lijnen van zijaanzicht om de totale hoogte van de pijp vast te stellen en lopen ze uit tot een lengte van 14,125″. Zodra we de hoogte en stretch-out compleet zijn zijn we klaar om de element lijnen te plaatsen.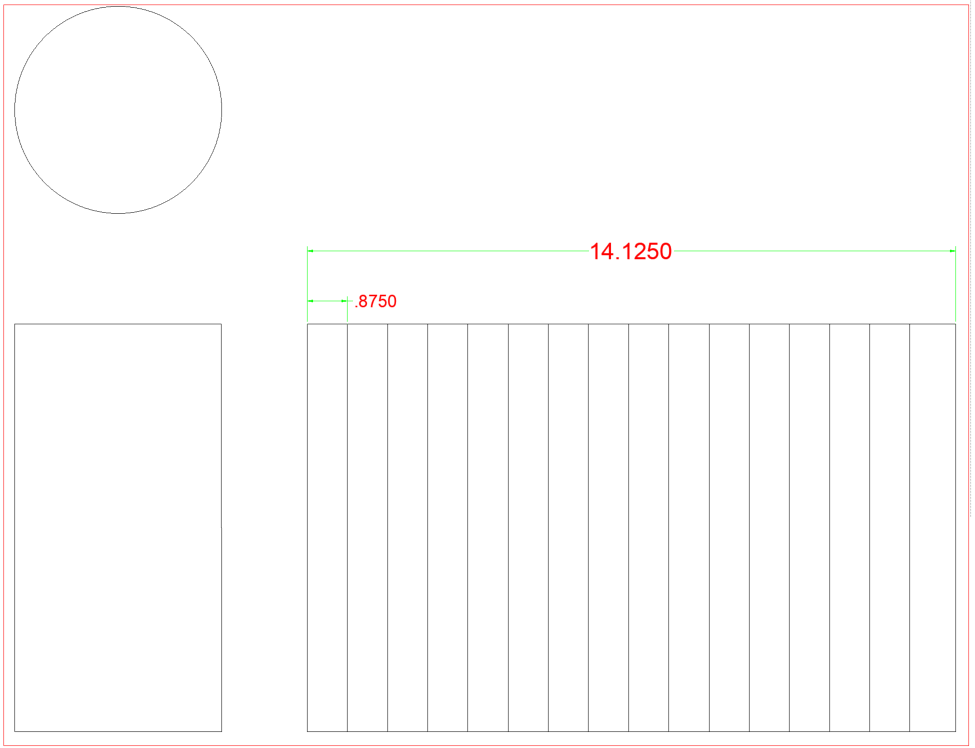
bij het werken met pipe en het ontwikkelen van sjablonen moet u wat basisgeometrie en het verdelen van hoeken bijwerken. We zullen een kompas gebruiken voor deze taak.
hieronder hebben we een hoekcabine met een hoekpunt van punt A.
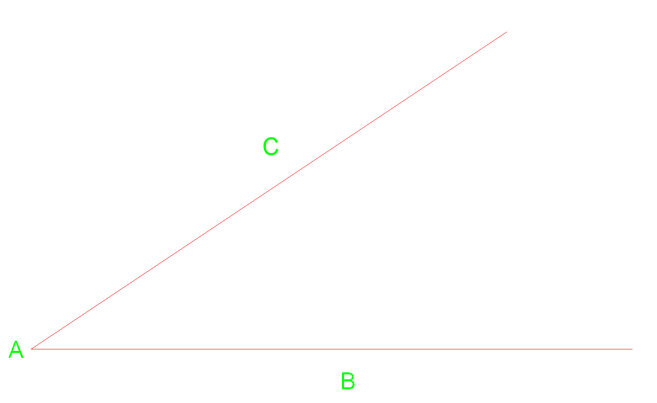
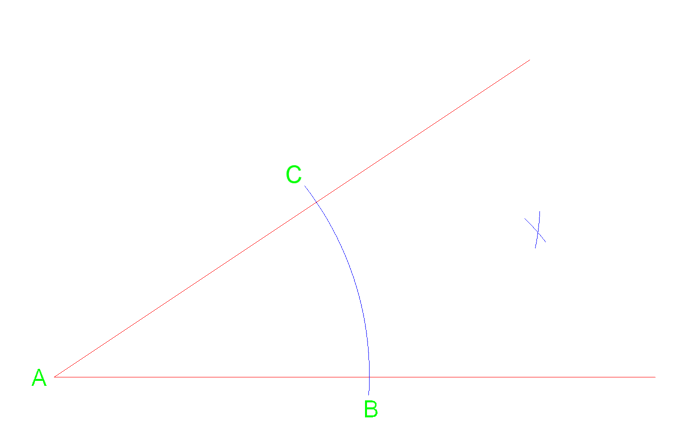
eerst kunnen we een boog tekenen van hoekpunt A die de lijn bij punt C & B kruist.van deze twee snijpunten kunnen we dan twee extra bogen naar rechts tekenen.
trek vanuit hoekpunt A een lijn die kruist op punt D waar de boog snijdt.
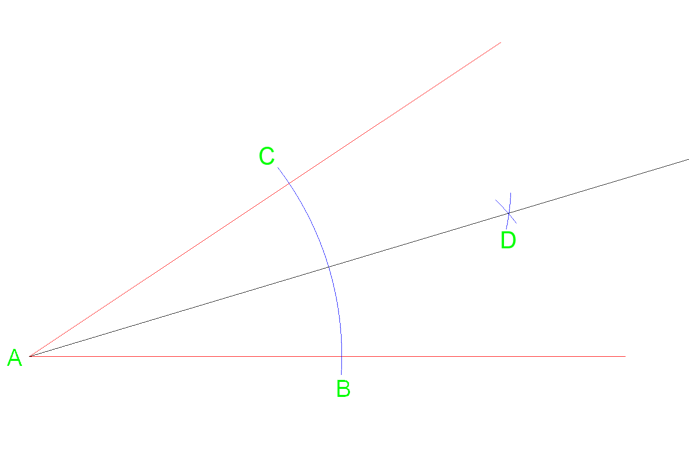
met behulp van deze methode zal de hoek gelijkelijk splitsen in twee hoek van dezelfde meting. Deze methode en kan herhaald indien nodig opnieuw te splitsen in 4 gelijke delen.
laten we een soortgelijke methode proberen op een cirkel. De getekende cirkel heeft een diameter van 3″ dus een straal van 1½”.
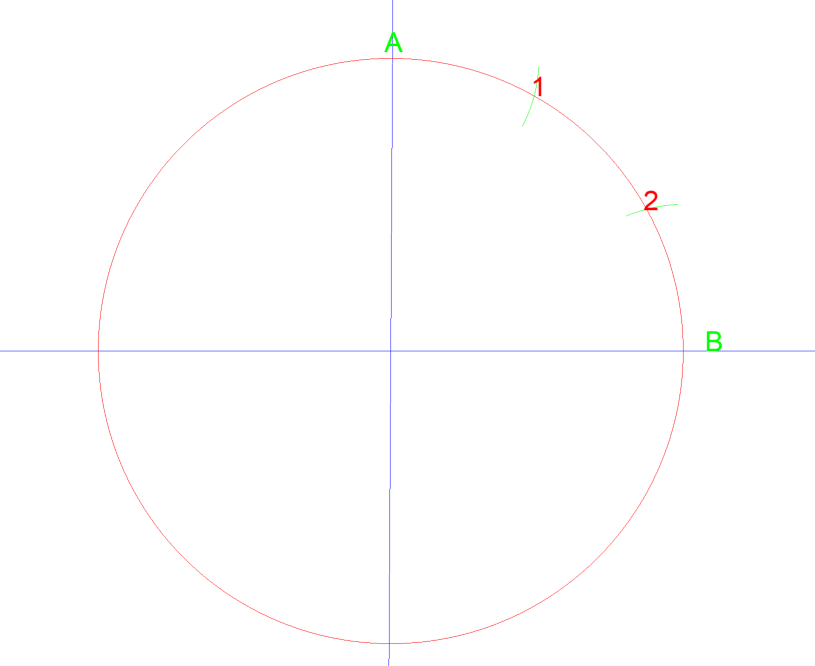
door je kompas in te stellen op de straal van de cirkel, 1 ½ ” en dan een boog te tekenen van punt A en dan B snijden ze op 1 & 2. Als je dan een lijn van het midden van de cirkel naar elk punt trekt, verdeelde je dat kwart van de cirkel in drie gelijke delen. Zie hieronder…
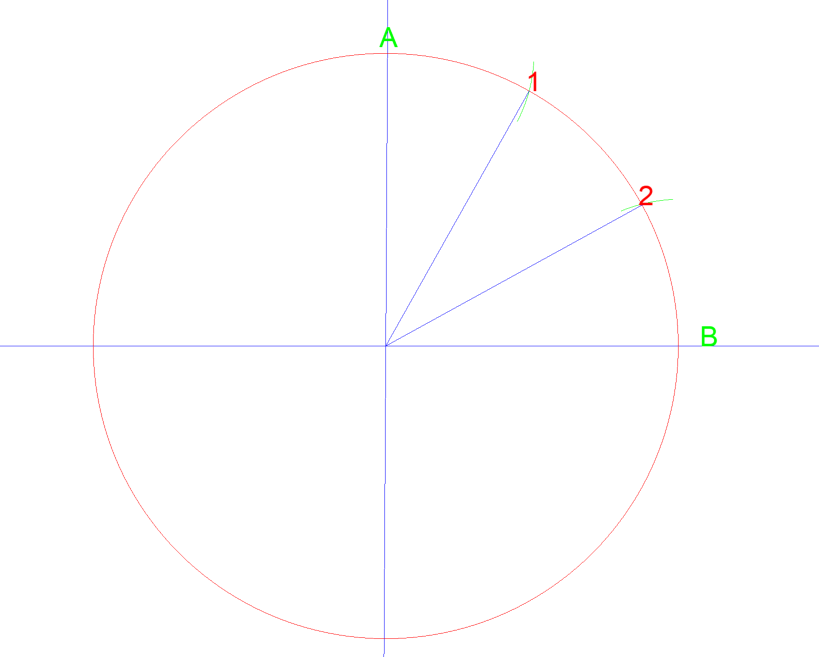
als je dit vervolgens weer deed tussen A, 1, 2, & B kun je dat kwart van een cirkel verdelen in 6 gelijke gebieden.
zoals we eerder kort hebben besproken, gebruiken we getallen om te helpen bij het opstellen van waar lijnen zullen verbinden. Deze lijnen worden gebruikt wanneer we twee of meer onderdelen samenvoegen om één assemblage te maken. Terwijl we doorgaan, zult u beter begrijpen hoe dit nummering systeem werkt.