circunferência e como encontrar
existem algumas maneiras de encontrar a circunferência de tubos e tubos redondos. Saber que a circunferência é a chave para construir modelos precisos para usar com pipe. Quanto mais precisos forem os seus números ao desenvolver estes template, melhor ajuste você terá. Como com qualquer coisa, a prática e a experiência na construção de modelos também irá aumentar a precisão.
o método mais utilizado para calcular a circunferência é usar a fórmula do diâmetro de Pi x. 6 “od round tube has a circumference of 18.85”. 6 “x Pi=18.85”. Quando se trata de trabalhar com pipe, você precisa estar ciente de que pipe é medida nominalmente. Isto significa que 6 “pipe is not 6” DOD. Felizmente, todos os fabricantes de tubos seguem um padrão e há um número incontável de tabelas e gráficos que listam todos os tamanhos de tubos e até mesmo incluem a circunferência de todos os tamanhos! Por favor, consulte o índice para localizar essas tabelas, gráficos e outras informações.
ao longo das próximas seções vamos começar a desenvolver modelos para uso com pipe. Não importa a complexidade do modelo, existem vários conceitos-chave que são usados com todos eles, incluindo a determinação da circunferência. Só vamos introduzir estes conceitos em detalhe uma vez, se você precisar de ajuda, por favor, consulte uma seção anterior.Vamos falar em dividir a circunferência do tubo em várias partes iguais que ajudarão a desenvolver o modelo. Vamos referir-nos a estas linhas como linhas de elementos. Quanto mais linhas de elementos você tem mais preciso o ajuste.
como foi afirmado anteriormente, há muitas maneiras que os artesãos descobriram soluções para problemas complexos, este é livro oferece uma dessas.
abaixo temos um tubo de 4″. Referindo-se ao gráfico, podemos ver que a overdose desse tubo é de 4,50″. Também no gráfico vemos que tem uma circunferência total de 14.125″. Para este livro, vamos dividir todas as circunferências em 16 espaços iguais nos quais se tornarão as linhas de elementos. O gráfico na parte de trás também nos mostra o espaço para dividir a circunferência em 16 partes, bem como 12, 8, 6, 4 e 2. Lembre-se, quanto mais linhas de elementos você tem, mais precisa será o seu modelo. Se não tivéssemos o gráfico, você teria que dividir a circunferência total pelo número de espaços necessários. Alguns arredondamentos serão necessários ao fazer isso, mas você precisa estar ciente de que estar fora 1/16″, 16 vezes vai acabar sendo off por um 1 completo”.Se dividir 14, 125 por 16, acaba em .883. A ficha no estado de trás .875. .875, ou 7/8 ” é muito mais fácil de trabalhar em uma medida de fita do que .883. A diferença é de cerca de 1/132 por linha, isso será aceitável.
para começar vamos desenhar uma vista lateral que irá mostrar a altura da nossa secção de tubo. Em seguida, precisamos desenhar o nosso stretch-out. Sabemos que a circunferência é 14.125. Podemos desenhar um verticais adjacentes a vista lateral de um tubo e, em seguida, estender as linhas horizontais (mostrado em vermelho), que são as linhas superior e inferior da vista lateral para estabelecer a altura total do tubo e executá-los fora para um comprimento de 14.125″. Uma vez que temos a altura e stretch-out completo Estamos prontos para colocar as linhas de elementos.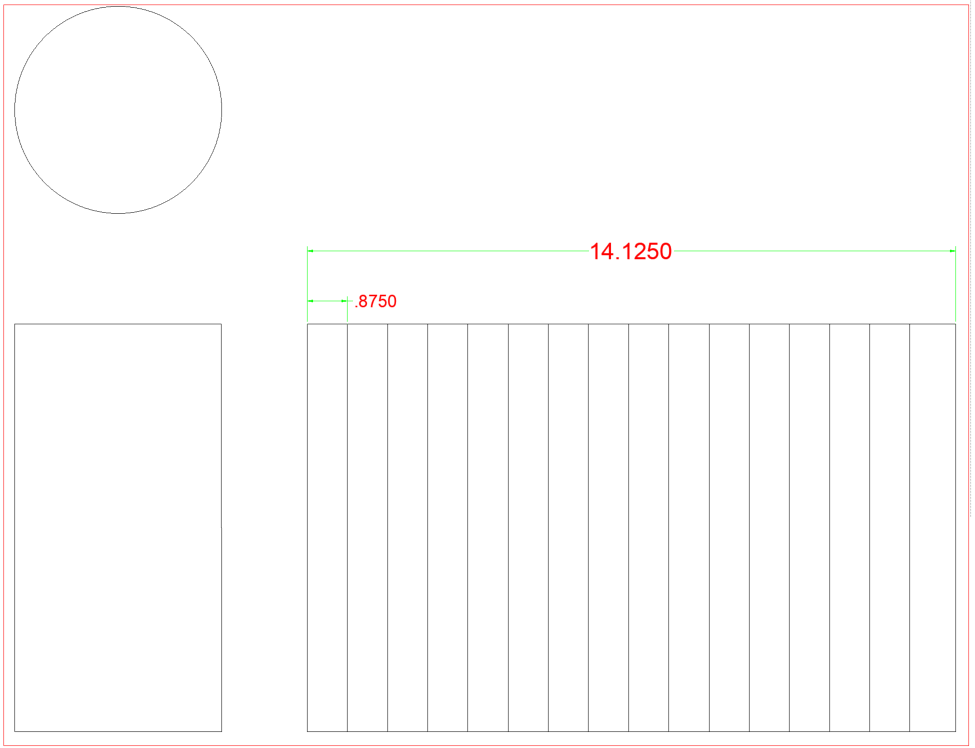
ao trabalhar com tubulações e modelos de desenvolvimento, terá de rever alguma geometria básica e a divisão dos ângulos. Vamos usar uma bússola para esta tarefa.Abaixo temos uma cabina angular com um vértice do ponto A.
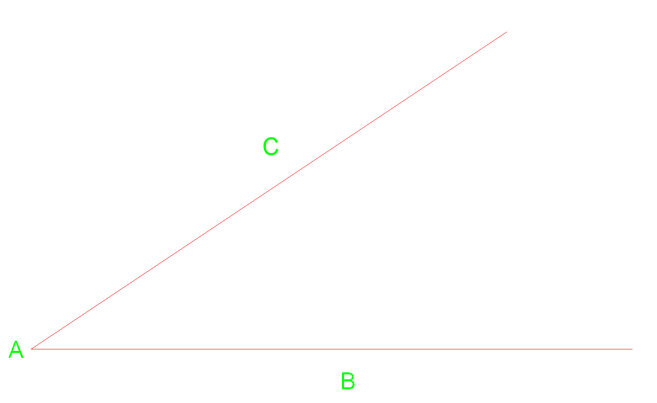
Primeiro podemos desenhar um arco de vértice a que cruza a linha perto do ponto C & B. A partir dessas duas intersecções podemos então desenhar dois arcos adicionais para a direita.
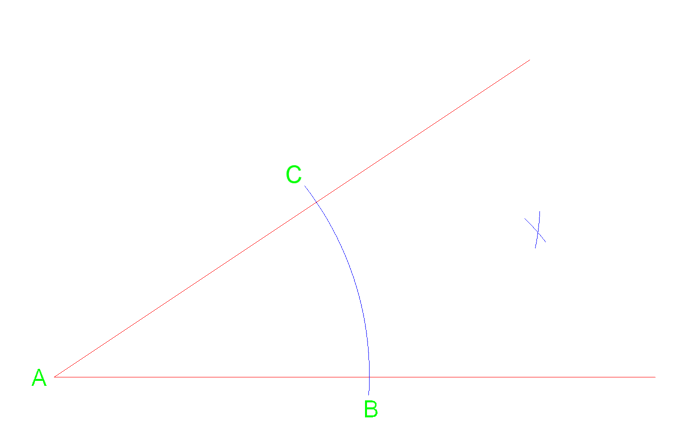
a partir do vértice um traço uma linha que cruza no ponto D onde o arco se intersecta.
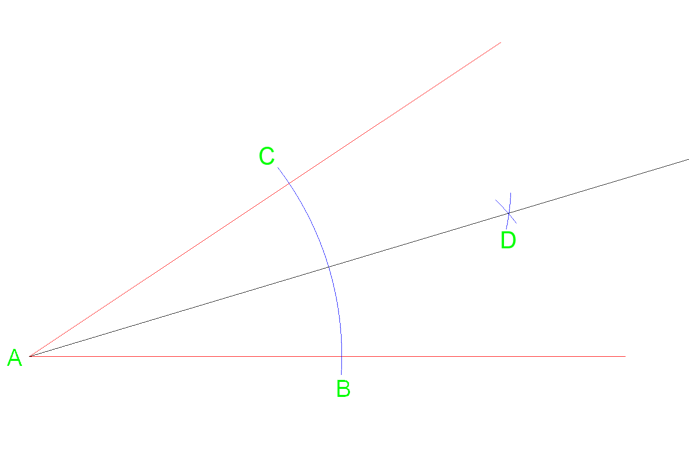
usando este método, dividirá igualmente o ângulo em dois ângulos da mesma medição. Este método e pode ser repetido se necessário para dividi-lo novamente em 4 partes iguais.
vamos tentar um método semelhante em um círculo. O círculo desenhado tem um diâmetro de 3 ” de modo que um raio de 1½”.
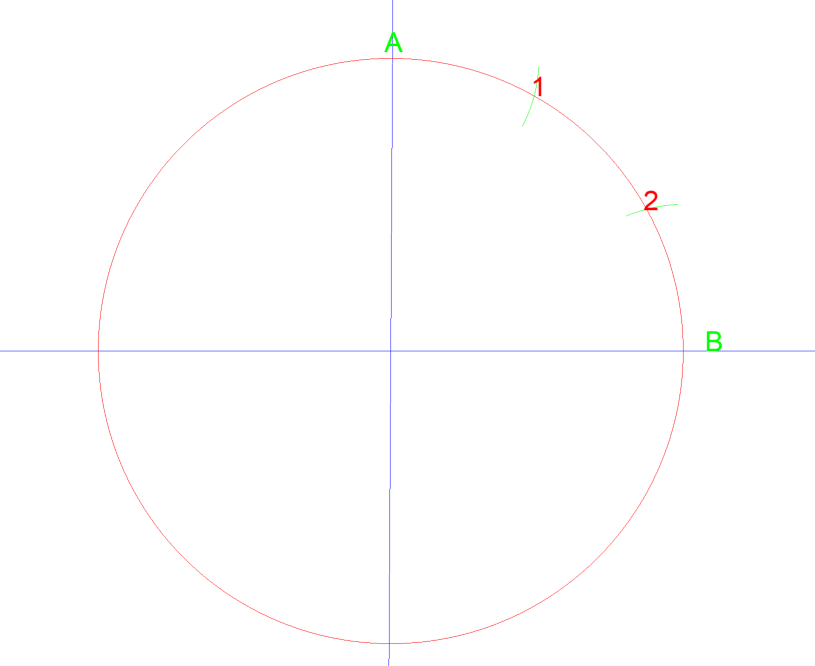
ao definir a sua bússola para o raio do círculo, 1 ½ ” e, em seguida, desenhar um arco a partir do ponto A e, em seguida, B eles se intersectam em 1 & 2. Se você então desenhar uma linha do centro do círculo para cada ponto, você apenas dividiu esse quarto do círculo em três partes iguais. Ver abaixo…
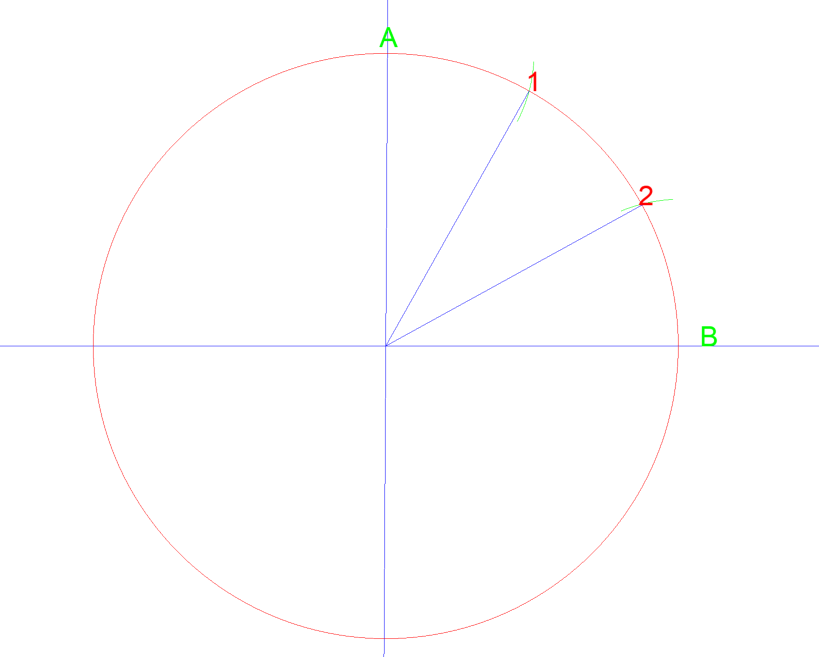
se você então fez isso novamente entre a, 1, 2, & B você pode dividir esse quarto de um círculo em 6 áreas iguais.
como cobrimos brevemente antes, usamos números para ajudar na formação de onde as linhas se conectarão. Estas linhas serão usadas quando estamos juntando duas ou mais partes para fazer uma montagem. À medida que continuamos, você vai entender melhor como este sistema de numeração funciona.