노암 초모스키에 따르면 문법에는 유형 0,유형 1,유형 2 및 유형 3 의 네 가지 유형이 있습니다. 다음 표에서는 서로 어떻게 다른지 보여 줍니다−
| 문법 유형 | 문법 허용 | 언어 허용 | 오토마톤 |
|---|---|---|---|
| 유형 0 | 무제한 문법 | 재귀 적으로 열거 가능한 언어 | 튜링 머신 |
| 유형 1 | 상황에 맞는 문법 | 상황에 맞는 언어 | 선형 경계 오토마톤 |
| 유형 2 | 문맥없는 문법 | 문맥없는 언어 | 푸시다운 오토마톤 |
| 유형 3 | 정규 문법 | 정규 언어 | 유한 상태 오토마톤 |
다음 그림을 살펴보십시오. 각 유형의 문법−
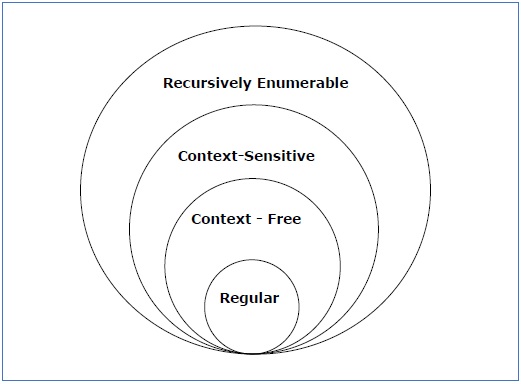
유형 3 문법
유형 3 문법은 일반 언어를 생성합니다. 유형 3 문법은 왼쪽에 단일 비 터미널이 있고 오른쪽은 단일 터미널 또는 단일 터미널 다음에 단일 비 터미널로 구성되어야합니다.
제작에 있어야 합니다 form X→X→aY
,X,Y∈N(비 터미널)
과∈T(터미널)
규칙 S→ε 이 허용되는 경우에 나타나지 않습니다 오른쪽의 어떤 규칙이 있습니다.
예제
X → ε X → a | aYY → b
유형 2 문법
유형 2 문법은 문맥 없는 언어를 생성합니다.
제작에 있어야 합성→γ
어디∈N(비 터미널)
고 γ∈(T∪N)*(문자열의 터미널 및 비 터미널).
이러한 문법에 의해 생성 된 이러한 언어는 비 결정적 푸시 다운 오토 마톤에 의해 인식됩니다.
예제
S → X a X → a X → aX X → abc X → ε
유형 1 문법
유형 1 문법은 상황에 맞는 언어를 생성합니다. 제작에 있어야 합 양식을
α β→α γ β
어디∈N(비 터미널)
고 α,β,γ∈(T∪N)*(문자열의 터미널 및 비 터미널)
문자열 α 및 β 이 비어 있을 수 있습니다,하지만 γ 이 비어있지 않아야 합.
규칙의 오른쪽에 표시되지 않는 경우 규칙이 허용됩니다. 이 문법에 의해 생성 된 언어는 선형 경계 오토 마톤에 의해 인식됩니다.
예제
AB → AbBc A → bcA B → b
유형 0 문법
유형 0 문법은 재귀 적으로 열거 가능한 언어를 생성합니다. 제작에는 제한이 없습니다. 모든 형식 문법을 포함한 모든 단계 구조 문법입니다.
그들은 튜링 기계에 의해 인식되는 언어를 생성합니다.
제작은 적어도 하나의 비 터미널을 가진 터미널 및 비터미널의 문자열이고,제 3 의 비터미널은 널일 수 없다. 이 문자열은 터미널과 비 터미널의 문자열입니다.
예
S → ACaB Bc → acB CB → DB aD → Db