Algoritmi FDTD e FDM per l’analisi MHOF
La luce ottica è un’onda elettromagnetica in natura, e quindi le sue proprietà di propagazione sono governate dalle leggi dell’elettrodinamica che sono note collettivamente come equazioni di Maxwell. È noto che la guida dei segnali luminosi nel MHOF con strutture bandgap fotoniche si basa sull’effetto di interferenza costruttiva dovuto alla disposizione periodica di fori d’aria identici. D’altra parte, quando i fori d’aria diventano casuali in termini di dimensioni, posizione o entrambi, avviene il fenomeno della riflessione interna totale e la differenza di indice tra il nucleo e il rivestimento fornisce il confinamento della luce e quindi la guida della luce lungo la fibra. Sebbene le caratteristiche di propagazione di strutture complicate come MHOF arbitrari non possano essere calcolate facilmente utilizzando metodi analitici, ci sono modi per risolvere numericamente i problemi elettromagnetici.
In questa sezione, due tecniche numeriche del dominio del tempo a differenza finita (FDTD) e del metodo delle differenze finite (FDM) sono affrontate considerando l’estensione all’analisi di fibre ottiche forate con distribuzioni arbitrarie di fori d’aria. Ognuna di queste tecniche ha alcuni vantaggi. Utilizzando il metodo FDTD, il campo elettromagnetico continuo in un volume finito di spazio viene campionato in punti distinti in un reticolo spaziale e in punti di campionamento equidistanti nel tempo. I dati campionati nei punti vengono utilizzati per i calcoli numerici delle modalità consentite, senza generare soluzioni di modalità spurie, in una determinata guida d’onda. Nonostante sia una tecnica efficace per il calcolo delle costanti di propagazione dei modi guidati, il metodo FDTD non è adatto per la valutazione delle singole distribuzioni di campo di modo. Questo perché la sorgente è una funzione di impulso nel dominio del tempo che copre uno spettro infinito, quindi le soluzioni di distribuzione del campo sono la sovrapposizione di tutti i modi possibili. Per ovviare a questo problema con le costanti di propagazione disponibili da FDTD, le distribuzioni di campo in modalità individuale sono ottenute utilizzando l’FDM, che può fornire rapidamente e comodamente soluzioni di campo in modalità individuale.
Il FDTD ha guadagnato una notevole popolarità negli ultimi anni, perché questo metodo fornisce soluzioni robuste, basate sulle equazioni di Maxwell , e può facilmente ospitare proprietà materiali di valore complesso. Un oggetto materiale arbitrario può essere approssimato costruendo celle unitarie per le quali le posizioni dei componenti del campo sono disposte con i valori desiderati di permittività e permeabilità. Una volta specificata la geometria dell’oggetto nella regione di simulazione numerica, la condizione di origine viene modellata da qualche parte nella regione. Inizialmente, si presume che tutti i campi all’interno del dominio di calcolo siano identicamente zero. Quindi, viene applicata un’onda incidente per immettere la regione di calcolo numerico.
Usando il sistema di unità MKS, consideriamo prima le equazioni di Maxwell espresse come:
dove ε è la permittività elettrica costante a F/m e m è la permeabilità magnetica costante in H/m. Ampliando il curl espressioni e paragonando la come componenti, il sistema di sei accoppiato equazioni differenziali alle derivate parziali sono formati per la FDTD analisi di onda elettromagnetica interazioni con generale oggetti tridimensionali. Va notato che i componenti del campo elettrico e magnetico (Ex, Ey, Ez, Hx, Hy e Hz) sono correlati. Cioè, le equazioni di Maxwell non producono direttamente i valori del campo elettrico e magnetico, ma piuttosto mettono in relazione la velocità di variazione tra i valori del campo elettrico e magnetico.
Adottando l’approssimazione a differenza finita centrale per le derivate spazio-temporali con precisione al secondo ordine, è possibile sviluppare le seguenti approssimazioni come esempi rappresentativi in una formulazione FDTD tridimensionale (3D) :
dove i, j, k e n sono numeri interi per Δx, Δy, Δz, e Δt, rispettivamente, come lo spazio e il tempo in incrementi .
Poiché le fibre ottiche come MHOFs non hanno generalmente variazioni lungo la direzione di propagazione e le variazioni delle proprietà del materiale sono limitate alle direzioni trasversali come mostrato in Figura 3, la formulazione FDTD 3D può essere semplificata per l’algoritmo FDTD bidimensionale compatto (2D). Usando la notazione dei fasori con la costante di propagazione assiale (β), le derivate parziali del primo ordine rispetto a z sono sostituite con-jß, perché la dipendenza da z dei campi è come exp (- jßz). E due campi adiacenti richiesti per le derivate del primo ordine nella regione dello spazio discretizzato possono essere rappresentati da un campo nel punto medio tra di loro. Sulla base di questi due fatti, si ottiene la seguente formulazione come esempio:
L’algoritmo 2D risultante sfrutta una significativa riduzione dell’allocazione della memoria del computer richiesta e del tempo di esecuzione. Pertanto, per il calcolo al computer di guide d’onda arbitrarie uniformi lungo la direzione di propagazione dell’onda, è sufficiente solo la modellazione delle sezioni trasversali delle guide d’onda.
Insieme a questo algoritmo efficiente, i supporti infiniti nello spazio 2D per un oggetto elettromagnetico arbitrario devono essere modellati con attenzione, poiché la memoria del computer è limitata nella regione di calcolo anche con la tecnologia avanzata corrente. Per modellare le regioni che si estendono all’infinito, un livello perfettamente abbinato (PML) come una condizione al contorno assorbente altamente efficace (ABC) è progettato al limite esterno del reticolo di un dominio di calcolo. Idealmente, il mezzo assorbente è solo spessa come poche cellule reticolari, altamente assorbente, reflectionless a tutte le onde d’urto, ed efficace su tutta la gamma di lunghezze d’onda operative.
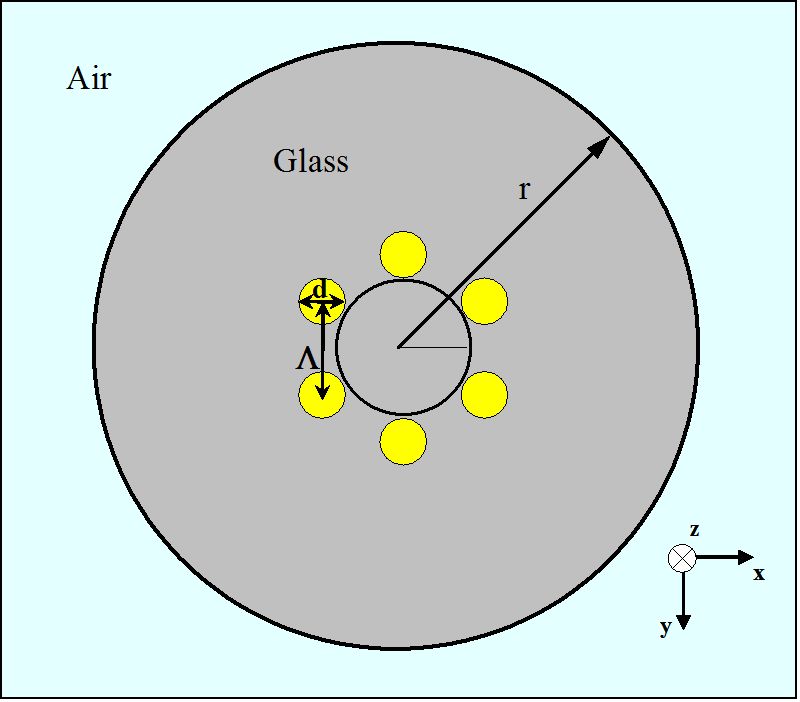
Figura 3.
Schema di una sezione trasversale per un MHOF con uno strato di fori per l’aria in una disposizione esagonale
Analogamente allo sviluppo dell’algoritmo FDTD, la formulazione FDM può essere derivata dalle equazioni di Maxwell accoppiate . Per le onde continue in media lineari e isotropi, combinando gli Eq (2) e (3) si ottiene la seguente equazione delle onde vettoriali:
dove n è l’indice di rifrazione e k0 è la costante di propagazione nello spazio libero. Molti dispositivi di guida d’onda, come le fibre ottiche, possono essere visti come strutture z-invarianti o a tratti z-invarianti. Per quelle strutture, l’indice di rifrazione n (x,y,z) varia lentamente lungo la direzione di propagazione z, che è valida per la maggior parte dei dispositivi a onde guidate fotoniche. Utilizzando il vettore di identità del∇×∇×=∇(∇⋅)−∇2, Eq (8) può essere scritto come
Anche con la ragionevole ipotesi di trascurabile dipendenza dal tempo lungo l’asse z, FDM formulazione come in Eq (9) può essere attuata mediante la sostituzione spaziale derivati con differenze finite approssimazioni. Qui, si nota che la componente trasversale (9) è
dove il pedice “t” sta per la trasversale componenti. Poiché la componente longitudinale può essere facilmente ottenuta applicando il seguente vincolo di divergenza zero (legge di Gauss) :
le componenti trasversali sono sufficienti per descrivere la natura full-vettoriale del campo elettromagnetico in una guida d’onda ottica.
Per l’indagine iniziale delle proprietà di orientamento di MHOFs, la fibra ottica indicata nella figura 3 è computer-analizzata. Generalmente, la geometria MHOF può essere descritta con due parametri, lunghezza passo (Λ) e diametro (d), come indicato nella Figura 3. Qui, la lunghezza del passo è la distanza tra i centri di due fori d’aria più vicini con la forma cilindrica. Per il MHOF di Figura 3, ogni piccolo foro d’aria ha un diametro di 1,4 µm, costituendo un esagono con Λ = 1,7 µm. La porzione di vetro che circonda i sei fori d’aria delle regioni gialle ha un indice di rifrazione di 1,45. Si presume che il raggio esterno (r) della fibra forata sia di 10 µm. Inoltre, la regione esterna del MHOF è l’aria.
Una volta definita la sezione trasversale di una fibra forata in un dominio di calcolo corretto, la simulazione FDTD può essere eseguita con diversi parametri specificati, come τ nella definizione di una sorgente gaussiana, Δt per la simulazione stabile, il numero totale (ntot) di passaggi temporali per il campionamento dei dati nel dominio del tempo e valori ragionevoli di β. Qui, al fine di evitare la divergenza numerica e garantire la stabilità dell’algoritmo FDTD, è necessario selezionare un Δt appropriato per soddisfare la seguente condizione di stabilità:
dove cM è la velocità massima di fase dell’onda all’interno di un dato modello numerico. Riassumendo il meccanismo alla base dell’analisi FDTD, la simulazione al computer procede con i seguenti passaggi:
-
Scegliere appropriati valori di parametro (t, ∆ T, ntot, e β)
-
il campionamento dei Dati di un campo di componente nel dominio del tempo
-
Prendere la trasformata di Fourier dei dati in tempo
-
Ottenere dati spettrali di un campo di componente
-
Modalità di prelievo frequenze associate con il valore di β
-
Raccogliere β e modalità di frequenza dei dati
-
Fare un appezzamento di modalità di indice e lunghezza d’onda
la Figura 4 illustra le curve caratteristiche, che sono ottenuti dal FDTD calcolo, per le prime tre modalità di ordine inferiore del MHOF definite nella Figura 3.
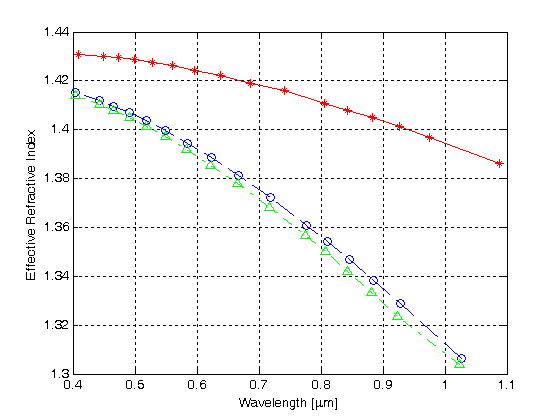
Figura 4.
Efficace indice di rifrazione rispetto di lunghezza d’onda per i primi tre modalità in un MHOF con uno strato di fori per l’aria
La curva rossa con le stelle, simboli trame normalizzato costante di propagazione per la prima modalità versus lunghezza d’onda, mentre il blu e il verde curve mostrano la normalizzato di propagazione delle costanti per la seconda e la terza modalità, rispettivamente. I risultati indicano che l’HMOF con un singolo strato esagonale del rivestimento del aria-foro sostiene la guida mista.