mi a klaszteranalízis?
a klaszterelemzés egy feltáró elemzés, amely megpróbálja azonosítani az adatokon belüli struktúrákat. A klaszterelemzést szegmentációs elemzésnek vagy taxonómiai elemzésnek is nevezik. Pontosabban megpróbálja azonosítani az esetek homogén csoportjait, ha a csoportosítás korábban nem ismert. Mivel feltáró jellegű, nem tesz különbséget függő és független változók között. Az SPSS által kínált különböző klaszterelemzési módszerek képesek kezelni a bináris, nominális, ordinális és skála (intervallum vagy Arány) adatokat.
a Klaszteranalízist gyakran használják más elemzésekkel (például diszkriminánsanalízissel) együtt. A kutatónak képesnek kell lennie a klaszterelemzés értelmezésére az adatok megértése alapján annak megállapítására, hogy az elemzés által előállított eredmények valóban értelmesek-e.
tipikus kutatási kérdések a klaszterelemzés válaszai a következők:
- orvostudomány-mik a diagnosztikai klaszterek? A kérdés megválaszolásához a kutató diagnosztikai kérdőívet dolgozna ki, amely magában foglalja a lehetséges tüneteket (például pszichológiában, szorongásban, depresszióban stb.). A klaszterelemzés ezután azonosíthatja a hasonló tünetekkel rendelkező betegcsoportokat.
- Marketing-melyek az ügyfélszegmensek? A kérdés megválaszolásához egy piackutató felmérést végezhet, amely lefedi az ügyfelek igényeit, attitűdjeit, demográfiai adatait és viselkedését. A kutató ezután felhasználhatja a klaszterelemzést a hasonló igényekkel és attitűdökkel rendelkező ügyfelek homogén csoportjainak azonosítására.
- Oktatás-melyek azok a diákcsoportok, amelyek különös figyelmet igényelnek? A kutatók mérhetik a pszichológiai, alkalmassági és teljesítményjellemzőket. A klaszterelemzés ezután azonosíthatja, hogy milyen homogén csoportok léteznek a hallgatók körében (például minden tantárgyban magasan teljesítők, vagy olyan hallgatók, akik bizonyos tantárgyakban kiemelkednek, de másokban kudarcot vallanak).
- Biológia-mi a fajok taxonómiája? A kutatók különböző növények adathalmazát gyűjthetik össze, és a fenotípusuk különböző tulajdonságait jegyezhetik fel. A klaszteranalízis csoportosíthatja ezeket a megfigyeléseket klaszterek sorozatába, és segíthet a hasonló növények csoportjainak és alcsoportjainak taxonómiájának felépítésében.
további technikák, amelyeket érdemes kipróbálni a hasonló megfigyelési csoportok azonosításához, a Q-analízis, a többdimenziós skálázás (MDS) és a látens osztályelemzés.
a klaszterelemzés az SPSS-ben
kutatási kérdésünk ebben a példában a klaszterelemzés a következő:
milyen homogén hallgatói klaszterek jelennek meg a matematika, az olvasás és az írás szabványosított teszteredményei alapján?
az SPSS Klaszterelemzésekben megtalálható az elemzés/osztályozás…. Az SPSS három módszert kínál a klaszterelemzéshez: k-azt jelenti, hogy klaszter, hierarchikus Klaszter és kétlépcsős klaszter.
a K-means cluster egy módszer a nagy adatkészletek gyors fürtözésére. A kutató előre meghatározza a klaszterek számát. Ez hasznos különböző modellek tesztelésére, eltérő feltételezett számú klaszterrel.
a hierarchikus klaszter a leggyakoribb módszer. Ez generál egy sor modellek klaszter megoldások 1 (minden esetben egy klaszter) n (minden esetben egy egyedi klaszter). A hierarchikus klaszter változókkal is működik, szemben az esetekkel; a faktorelemzéshez némileg hasonló módon csoportosíthatja a változókat. Ezenkívül a hierarchikus klaszterelemzés képes kezelni a nominális, ordinális és skálaadatokat; azonban nem ajánlott a különböző mérési szintek keverése.
a kétlépcsős klaszteranalízis a csoportosulásokat először az előcsoportosítás, majd a hierarchikus módszerek futtatásával azonosítja. Mivel egy gyors klaszter algoritmust használ előre, képes kezelni a nagy adathalmazokat, amelyek hierarchikus klasztermódszerekkel történő kiszámítása hosszú időt vesz igénybe. Ebben a tekintetben az előző két megközelítés kombinációja. A kétlépcsős fürtözés képes kezelni a méretarányos és sorszámos adatokat ugyanabban a modellben, és automatikusan kiválasztja a klaszterek számát.
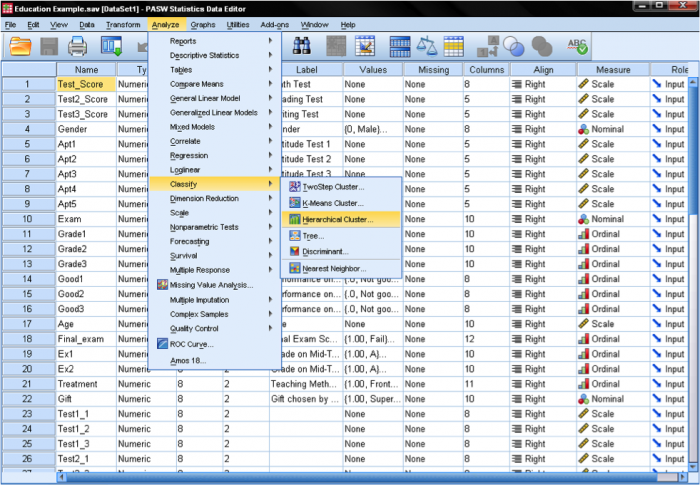
a hierarchikus klaszterelemzés három alapvető lépést követ: 1) számítsa ki a távolságokat, 2) kapcsolja össze a fürtöket, és 3) válasszon megoldást a megfelelő számú klaszter kiválasztásával.
először ki kell választanunk azokat a változókat, amelyekre klasztereinket alapozzuk. A párbeszédablakban hozzáadjuk a matematikai, olvasási és írási teszteket a változók listájához. Mivel az eseteket csoportosítani akarjuk, a többi kullancsot alapértelmezetten hagyjuk.
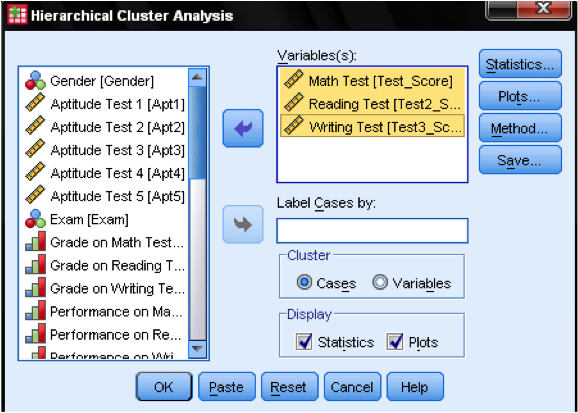
a párbeszédpanelen statisztika … megadhatjuk, hogy ki akarjuk-e adni a közelségi mátrixot (ezek az elemzés első lépésében kiszámított távolságok), valamint az esetek előrejelzett klasztertagságát megfigyeléseinkben. Ismét az összes beállítást alapértelmezés szerint hagyjuk.

a párbeszédpanelen telkek … hozzá kell adnunk a Dendrogramot. A dendrogram grafikusan megmutatja, hogyan egyesülnek a klaszterek, és lehetővé teszi számunkra, hogy meghatározzuk a megfelelő számú klasztert.
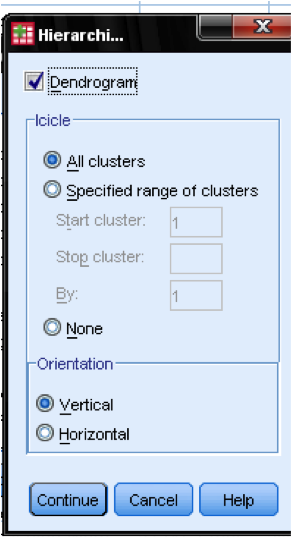
a párbeszédpanel metódusa … lehetővé teszi számunkra, hogy megadjuk a távolságmérést és a fürtözési módszert. Először meg kell határoznunk a helyes távolságmérést. Az SPSS három nagy blokknyi távolságmérőt kínál az intervallum (skála), a számlálás (ordinális) és a bináris (névleges) adatok számára.
az intervallumadatok esetében a leggyakoribb a négyzet euklideszi távolság. Két megfigyelés közötti euklideszi távolságon alapul, amely a négyzet távolságok összegének négyzetgyöke. Mivel az euklideszi távolság négyzet alakú, növeli a nagy távolságok fontosságát, miközben gyengíti a kis távolságok fontosságát.

ha van rendes adatunk (számlálás), választhatunk a Chi-négyzet vagy a szabványosított Chi-négyzet között, amelyet Phi-négyzetnek nevezünk. Bináris adatok esetén általában a négyzet euklideszi távolságot használják.

példánkban az intervallum és a négyzet euklideszi távolságot választjuk.
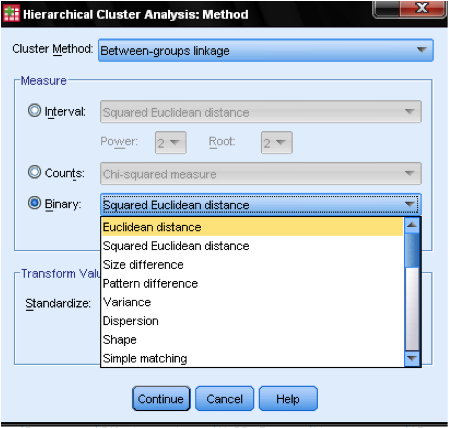
ezután ki kell választanunk a klaszter módszert. A választás általában a csoportok közötti kapcsolat (a klaszterek közötti távolság az ezen klasztereken belüli összes adatpont átlagos távolsága), a legközelebbi szomszéd (egyetlen kapcsolat: a klaszterek közötti távolság a legkisebb távolság két adatpont között), a legtávolabbi szomszéd (teljes kapcsolat: a távolság a legnagyobb távolság két adatpont között), és Ward módszere (a távolság az összes klaszter távolsága a minta Nagy átlagához). Az egykötés a klaszterek hosszú láncaival működik a legjobban, míg a teljes összekapcsolás a klaszterek sűrű foltjaival működik a legjobban. A csoportok közötti kapcsolat mindkét fürttípussal működik. Javasoljuk, hogy először használjon egyetlen összeköttetést. Bár az egyetlen kapcsolat hajlamos klaszterláncokat létrehozni, segít a kiugró értékek azonosításában. Miután kizártuk ezeket a kiugró értékeket, áttérhetünk Ward módszerére. Ward módszere az F értéket használja (mint az ANOVA – ban), hogy maximalizálja a klaszterek közötti különbségek jelentőségét.
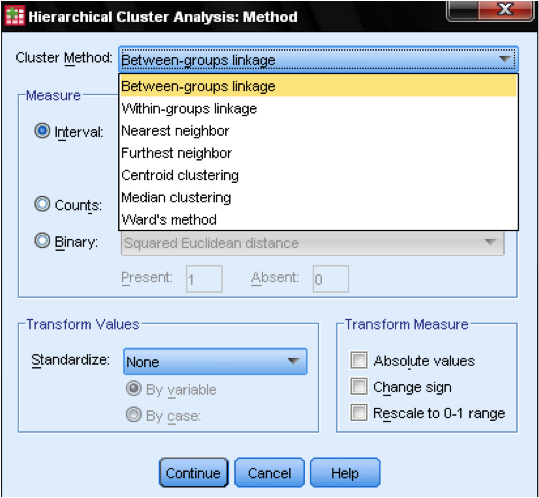
az utolsó szempont a szabványosítás. Ha a változók különböző skálákkal rendelkeznek, és azt jelenti, hogy esetleg z pontszámokra vagy a skála központosításával szeretnénk szabványosítani. Az értékeket abszolút értékekké is átalakíthatjuk, ha van olyan adatkészletünk, ahol ez megfelelő lehet.