FDTD és FDM algoritmusok az MHOF elemzéshez
az optikai fény elektromágneses hullám jellegű, ezért terjedési tulajdonságait az elektrodinamika törvényei szabályozzák, amelyeket együttesen Maxwell-egyenleteknek neveznek. Ismeretes, hogy a fényjelek irányítása az MHOF-ban fotonikus sávtartó szerkezetekkel konstruktív interferencia hatásra támaszkodik az azonos léglyukak időszakos elrendezése miatt. Másrészt, amikor a léglyukak mérete, elhelyezkedése vagy mindkettő véletlenszerűvé válik, a teljes belső visszaverődés jelensége megtörténik, és a mag és a burkolat közötti indexkülönbség fényzárást és így a fény vezetését biztosítja a szál mentén. Bár az olyan bonyolult struktúrák terjedési jellemzői, mint az önkényes Mhof-ok, analitikai módszerekkel nem számíthatók ki könnyen, vannak módok az elektromágneses problémák numerikus megoldására.
ebben a szakaszban a véges különbségű időtartomány (FDTD) és a véges különbség módszer (FDM) két numerikus technikájával foglalkozunk, figyelembe véve a lyukas optikai szálak tetszőleges levegő-lyuk eloszlású elemzésének kiterjesztését. Ezen technikák mindegyikének vannak bizonyos előnyei. Az FDTD módszer alkalmazásával a véges térfogatú térben lévő folytonos elektromágneses mezőt a térrács különböző pontjain és az időben egyenlő távolságra lévő mintavételi pontokon veszik fel. A pontok mintavételezett adatait a megengedett módok numerikus számításaihoz használják, hamis módú megoldások generálása nélkül, egy adott hullámvezetőben. Annak ellenére, hogy hatékony módszer az irányított üzemmódok terjedési állandóinak kiszámítására, az FDTD módszer nem alkalmas az egyes módmezők eloszlásainak értékelésére. Ez azért van, mert a forrás egy impulzusfüggvény az időtartományban, amely végtelen spektrumot fed le, így a téreloszlási megoldások az összes lehetséges mód szuperpozíciója. Az FDTD-ből elérhető terjedési állandókkal kapcsolatos probléma enyhítése érdekében az FDM segítségével egyedi módú mezőeloszlásokat kapunk, amelyek gyorsan és kényelmesen nyújthatnak egyedi módú mező megoldásokat.
az FDTD jelentős népszerűségre tett szert az elmúlt években, mivel ez a módszer robusztus megoldásokat kínál, Maxwell egyenletein alapulva , és könnyen képes befogadni a komplex értékű anyagtulajdonságokat. Egy tetszőleges anyagobjektum közelíthető olyan egységcellák felépítésével, amelyekhez a mező komponens pozíciói a kívánt permittivitási és permeabilitási értékekkel vannak elhelyezve. Amint az objektum geometriája meg van adva a numerikus szimulációs régióban, a forrásfeltétel modellezése valahol a régióban történik. Kezdetben feltételezzük, hogy a számítási tartományon belüli összes mező azonos nulla. Ezután egy eseményhullám kényszerül a numerikus számítási régióba való belépésre.
az MKS egységrendszer használatával először vizsgáljuk meg Maxwell curl-egyenleteit:
ahol a H/M-ben az elektromos permittivitási állandó, H/M-ben pedig a mágneses permeabilitási állandó. Meg kell jegyezni, hogy az elektromos és mágneses mező komponensei (Ex, EY, Ez, Hx, Hy és Hz) összefüggenek egymással. Ez azt jelenti, hogy a Maxwell-egyenletek nem közvetlenül adják meg az elektromos és a mágneses mező értékeit, hanem inkább az elektromos és a mágneses mező értékei közötti változás sebességét kapcsolják össze.
a tér-és időszármazékok központi véges differencia közelítésének másodrendű pontossággal történő elfogadásával a következő közelítések reprezentatív példákként kidolgozhatók egy háromdimenziós (3D) FDTD formulában:
, ahol i, j, k, n egész számok vannak a Δx, Δy, Δz, valamint Δt volt, mint a tér-idő-os lépésekben .
mivel az olyan optikai szálaknak, mint az Mhof-ok, általában nincsenek variációik a terjedési irány mentén, és az anyagtulajdonságok variációi a 3 .ábrán látható keresztirányokra korlátozódnak, a 3D FDTD megfogalmazás egyszerűsíthető a kompakt kétdimenziós (2D) FDTD algoritmusra. A phasor jelöléssel az axiális terjedési állandóval (xhamsterrel) az elsőrendű parciális deriváltakat Z-vel helyettesítjük-J vállalkozók, mert a mezők z-függősége olyan exp (- J xhamz). A diszkretizált térrész elsőrendű deriváltjaihoz szükséges két szomszédos mezőt pedig a köztük lévő középpontban lévő mező ábrázolhatja. E két tény alapján a következő megfogalmazást kapjuk példaként:
az eredményül kapott 2D algoritmus kihasználja a szükséges számítógépes memória allokáció és futási idő jelentős csökkenését. Így a hullámterjedés irányában egyenletes tetszőleges hullámvezetők számítógépes kiszámításához csak a hullámvezetők keresztmetszeteinek modellezése elegendő.
ezzel a hatékony algoritmussal együtt gondosan modellezni kell a 2D térben lévő végtelen adathordozókat egy tetszőleges elektromágneses tárgy számára, mert a számítógépes memória korlátozott a számítási régióban még a fejlett jelenlegi technológiával is. A végtelenségig terjedő régiók modellezése érdekében egy tökéletesen illeszkedő réteget (PML), mint rendkívül hatékony abszorbeáló határfeltételt (ABC) terveztek a számítási tartomány külső rácshatárán. Ideális esetben az abszorbeáló közeg csak olyan vastag, mint néhány rácssejt, erősen abszorbeáló, visszaverődésmentes minden ütköző hullám számára, és hatékony a működési hullámhossz teljes tartományában.
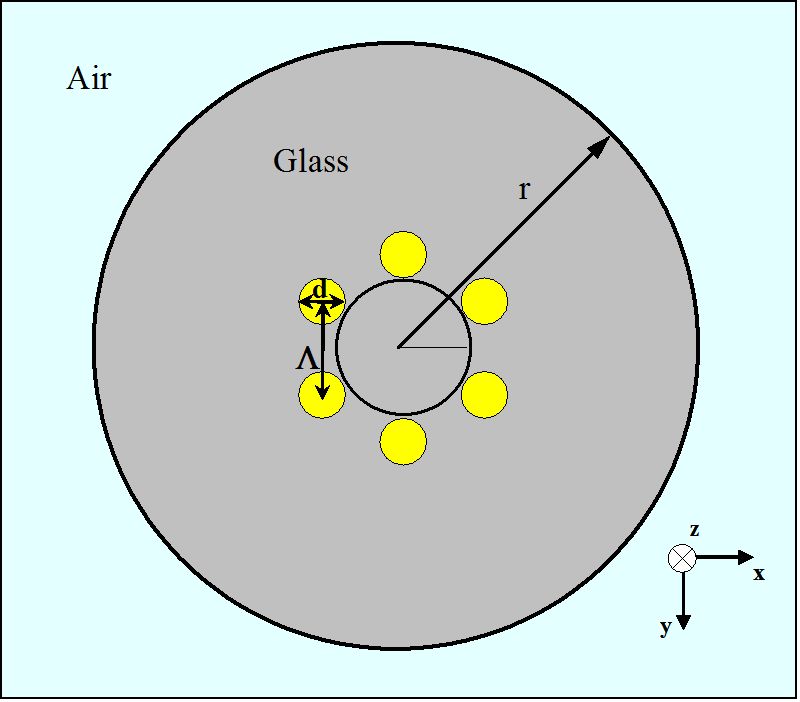
3. ábra.
az MHOF keresztmetszetének vázlata egy hatszögletű elrendezésű léglyukakkal
az FDTD algoritmus kifejlesztéséhez hasonlóan az FDM megfogalmazás levezethető a csatolt Maxwell-egyenletekből . Lineáris és izotróp közegben lévő folytonos hullámok esetén az Eqs (2) és (3) kombinálása a következő vektoriális hullámegyenletet eredményezi:
ahol n a törésmutató, k0 pedig a terjedési állandó a szabad térben. Számos hullámvezető eszköz, például optikai szálak, úgy tekinthető z-invariáns, vagy darabonként z-invariáns struktúrák. Ezen struktúrák esetében a törésmutató n (x,y, z) lassan változik a terjedési irány mentén z, ami a legtöbb fotonikus irányított hullámú eszközre érvényes. A vektorazonosság használatával∇×∇×=∇(∇⋅)−∇2, Az Eq (8)írható:
A Z tengely mentén elhanyagolható időfüggőség ésszerű feltételezésével az EQ (9) szerinti FDM megfogalmazás megvalósítható úgy, hogy a térbeli deriváltakat véges különbség-közelítésekkel helyettesítjük. Itt meg kell jegyezni, hogy a transzverzális komponens (9) az
, ahol az alsó index “t” – áll a keresztirányú alkatrészek. Mivel a longitudinális komponens könnyen előállítható a következő nulla divergencia alkalmazásával (Gauss-törvény) kényszer:
a keresztirányú komponensek elegendőek az elektromágneses mező teljes vektoriális természetének leírására egy optikai hullámvezetőben.
az Mhof-ok irányító tulajdonságainak kezdeti vizsgálatához a 3.ábrán látható optikai szálat számítógéppel elemezzük. Az MHOF-geometria általában két paraméterrel írható le, a hangmagasság hosszával (6) és az átmérővel (d), amint azt a 3.ábra mutatja. Itt a hangmagasság hossza a henger alakú két legközelebbi léglyuk középpontja közötti távolság. A MHOF a 3. Ábra, minden kis levegő lyuk átmérője 1,4 µm, alkotó egy hatszög a Λ = 1.7 µm. A sárga régiók hat léglyukát körülvevő üvegrész törésmutatója 1,45. Feltételezzük, hogy a lyukas szál külső sugara (r) 10 MHz. Az MHOF külső régiója is levegő.
miután a lyukas szál keresztmetszetét egy megfelelő számítási tartományban meghatározták, az FDTD szimuláció több meghatározott paraméterrel is elvégezhető, például a Gauss-forrás meghatározásakor a causs-forrás, a stabil szimuláció esetén a Caust, az időlépések teljes száma (ntot) az időtartományban lévő adatok mintavételéhez, és a ésszerű értékek a caustd. Itt a numerikus divergencia elkerülése és az FDTD algoritmus stabilitásának biztosítása érdekében a következő stabilitási feltétel kielégítéséhez ki kell választani egy megfelelő:
ahol cM a maximális hullámfázis-sebesség egy adott numerikus modellen belül. Összefoglalva az FDTD elemzés mögött meghúzódó mechanizmust, a számítógépes szimuláció a következő lépésekkel folytatódik:
-
válassza ki a megfelelő paraméterértékeket)
-
az időtartományban lévő mezőösszetevő adatmintázása
-
Vegyük az időadatok Fourier-transzformációját
-
egy mező összetevő spektrális adatainak lekérése
-
pick mód frekvenciák társított a ++ érték
-
gyűjtsük össze a frekvenciaadatokat és a frekvenciaadatokat
-
Készíts egy telek mód index versus hullámhossz
a 4. ábra a jellemző görbéket szemlélteti, amelyeket az FDTD-ből kapunk számítás, a 3. ábrán meghatározott MHOF első három alacsonyabb rendű módjára.
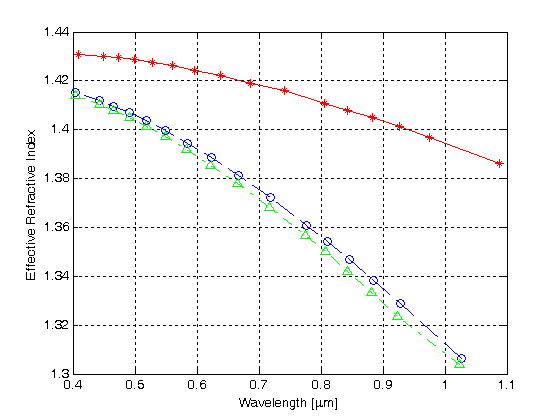
4. ábra.
hatékony törésmutató a hullámhosszhoz képest az MHOF első három üzemmódjában, egy réteg léglyukkal
a csillag szimbólumokkal ellátott piros görbe az első mód normalizált terjedési állandóját ábrázolja a hullámhossz függvényében,míg a kék és a zöld görbe a második, illetve a harmadik mód normalizált terjedési állandóit mutatja. Az eredmények azt mutatják, hogy az egyetlen hatszögletű léglyuk burkolóréteggel ellátott HMOF támogatja a multimódusú vezetést.