Katamorfismi jommallekummalle on sen taitoksen yleistys. Katamorfismi mahdollistaa toiminnot, joita ei ole saatavilla Foldin kautta.
tämä artikkeli on osa katamorfismeja käsittelevää artikkelisarjaa. Katamorfismi on universaalinen abstraktio, joka kuvaa, miten tietorakenne sulatetaan mahdollisesti kompaktimmaksi arvoksi.
tässä artikkelissa esitetään katamorfismi jommallekummalle (tunnetaan myös nimellä tulos), sekä miten se voidaan tunnistaa. Tämän artikkelin alussa esitellään C#: n katamorfismi esimerkein. Artikkelin loppuosassa kuvataan, miten katamorfismi voidaan päätellä. Tämä osa artikkelista esittelee työtäni Haskellissa. Lukijat, jotka eivät ole tyytyväisiä Haskelliin, voivat vain lukea ensimmäisen osan ja pitää artikkelin loppuosaa valinnaisena liitteenä.
joko on datasäiliö, joka mallintaa kaksi toisensa poissulkevaa tulosta. Sitä käytetään usein palauttaa arvoja, jotka voivat olla joko oikea (Oikea), tai virheellinen (vasen). Staattisesti tyypitetyssä funktionaalisessa ohjelmoinnissa, jossa suositaan kokonaisfunktioita, joko tarjoaa järkevämmän, järkevämmän tavan mallintaa menestystä ja virhetuloksia kuin heittämällä poikkeuksia.
C# katamorfismi #
tässä artikkelissa käytetään kirkon koodausta joko. Katamorfismi jommallekummalle on Match – menetelmä:
T Match<T>(Func<L, T> onLeft, Func<R, T> onRight);
tähän artikkeliin asti kaikki aiemmat katamorfismit ovat olleet alkuarvosta ja funktiosta muodostettuja pareja. Jompikumpi katamorfismi on yleistys, koska se on funktiopari. Yksi funktio käsittelee tapausta, jossa on vasen arvo, ja toinen funktio käsittelee tapausta, jossa on oikea arvo. Molempien funktioiden on palautettava sama, yhdistävä tyyppi, joka on usein merkkijono tai jotain vastaavaa, joka voidaan näyttää käyttöliittymässä:
> IEither<TimeSpan, int> e = new Left<TimeSpan, int>(TimeSpan.FromMinutes(3));> e.Match(ts => ts.ToString(), i => i.ToString())"00:03:00"> IEither<TimeSpan, int> e = new Right<TimeSpan, int>(42);> e.Match(ts => ts.ToString(), i => i.ToString())"42"
näet usein esimerkkejä, kuten edellä, joka kääntyy sekä vasemmalle ja oikealle tapauksissa merkkijonoja tai jotain, joka voidaan esittää yhdistävä vastaus tyyppi, mutta tämä ei ole millään tavalla vaaditaan. Jos voit keksiä yhdistävän tyypin, voit muuntaa molemmat tapaukset kyseiseen tyyppiin:
> IEither<Guid, string> e = new Left<Guid, string>(Guid.NewGuid());> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)12> IEither<Guid, string> e = new Right<Guid, string>("foo");> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)3
kahdessa yllä olevassa esimerkissä käytetään kahta eri funktiota, jotka molemmat pienentävät vastaavasti Guid ja string arvot luvuksi. Funktio, joka muuttaa Guid arvot luvuksi, laskee, kuinka monta Heksadesimaalilukua on suurempi tai yhtä suuri kuin A (10). Toinen funktio yksinkertaisesti palauttaa pituuden string, jos se on olemassa. Tuossa esimerkissä ei ole juurikaan järkeä, mutta Match – metodi ei siitä välitä.
käytännön käytössä jompaakumpaa käytetään usein virheiden käsittelyyn. Jommankumman kirkon koodausta käsittelevässä artikkelissa on esimerkki.
joko F-Algebra #
kuten edellisessä artikkelissa, käytän Fix ja cata kuten Bartosz Milewskin erinomaisessa artikkelissa F-Algebroja selitettiin.
vaikka rekursiivisille tietorakenteille käytetään enimmäkseen F-Algebroja ja kiinteitä pisteitä, voidaan F-Algebra määritellä myös ei-rekursiiviselle tietorakenteelle. Näitte jo esimerkin siitä artikkeleissa Boolen katamorfismista ja ehkä katamorfismista. Ero esim. ehkä-arvojen ja jommankumman välillä on se, että molemmissa tapauksissa jommallakummalla on arvo. Voit mallintaa tämän arvoksi Functor sekä kantoaaltotyypin että kahden tyypin argumentin avulla tiedoille, jotka joko voivat sisältää:
data EitherF l r c = LeftF l | RightF r deriving (Show, Eq, Read) instance Functor (EitherF l r) where fmap _ (LeftF l) = LeftF l fmap _ (RightF r) = RightF r
valitsin nimeksi ”tietotyypit” l (vasen) ja r (oikea) sekä kantotyypin c (oikea). Kuten myös BoolF ja MaybeF, Functor instanssi jättää karttafunktion huomiotta, koska kantajatyyppi puuttuu sekä LeftF tapauksesta että RightF tapauksesta. Kuten Functor esiintymät BoolF ja MaybeF, näyttäisi siltä, että mitään ei tapahdu, mutta tyyppitasolla tämä on edelleen käännös EitherF l r c – EitherF l r c1. Ei kummoinen funktio, ehkä, mutta ehdottomasti endofunktor.
kuten myös ehkä-ja Listakatamorfismeja päätellessä, Haskell ei ole kovin tyytyväinen instanssien määrittelyyn tyypille, kuten Fix (EitherF l r). Ongelman ratkaisemiseksi voit ottaa käyttöön newtype – kääreen:
newtype EitherFix l r = EitherFix { unEitherFix :: Fix (EitherF l r) } deriving (Show, Eq, Read)
voit määritellä Functor, Applicative, Monad, jne. instanssit tämän tyyppinen turvautumatta mitään funky GHC laajennuksia. Muista, että loppujen lopuksi, tarkoitus kaikki tämä koodi on vain selvittää, mitä katamorfismi näyttää. Tätä koodia ei ole tarkoitettu varsinaiseen käyttöön.
auttava funktiopari helpottaa EitherFix arvojen määrittelyä:
leftF :: l -> EitherFix l rleftF = EitherFix . Fix . LeftF rightF :: r -> EitherFix l rrightF = EitherFix . Fix . RightF
näillä funktioilla voidaan luoda EitherFix arvoja:
Prelude Data.UUID Data.UUID.V4 Fix Either> leftF <$> nextRandomEitherFix {unEitherFix = Fix (LeftF e65378c2-0d6e-47e0-8bcb-7cc29d185fad)}Prelude Data.UUID Data.UUID.V4 Fix Either> rightF "foo"EitherFix {unEitherFix = Fix (RightF "foo")}
muuta katamorfismin tunnistamiseen ei tarvita.
Haskellin katamorfismi #
tässä vaiheessa on kaksi kolmesta F-algebran alkiosta. Sinulla on endofunctori (EitherF l r) ja objekti c, mutta sinun täytyy silti löytää morfismi EitherF l r c -> c. Huomaa, että algebra, joka sinun täytyy löytää, on funktio, joka pelkistää functorin kantotyypilleen c, ei ”tietotyypit” l ja r. Tähän tottuminen vie aikaa, mutta niin katamorfismit toimivat. Tämä ei kuitenkaan tarkoita, etteikö l ja r saisi ohittaa, kuten nähdään.
kuten edellisissä artikkeleissa, aloita kirjoittamalla funktio, joka muuttuu katamorfismiksi, perustuen cata:
eitherF = cata alg . unEitherFix where alg (LeftF l) = undefined alg (RightF r) = undefined
vaikka tämä koostaa, sen undefined toteutukset, se ei ilmeisesti tee mitään hyödyllistä. Huomaan kuitenkin, että se auttaa minua ajattelemaan. Miten LeftF tapauksesta voi palauttaa arvon, jonka tyyppi on c? Voit siirtää argumentin funktiolle eitherF :
eitherF fl = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = undefined
vaikka voisit teknisesti siirtää c – tyypin argumentin eitherF: lle ja palauttaa tämän arvon LeftF tapauksesta, se tarkoittaisi, että jättäisit l: n arvon huomiotta. Tämä olisi virheellinen, joten sen sijaan tehdään argumentista funktio ja kutsutaan sitä merkillä l. Samoin RightF tapausta voi käsitellä samalla tavalla:
eitherF :: (l -> c) -> (r -> c) -> EitherFix l r -> ceitherF fl fr = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = fr r
tämä toimii. Koska cata on tyyppi Functor f => (f a -> a) -> Fix f -> a, se tarkoittaa, että alg on tyyppi f a -> a. EitherF tapauksessa kääntäjä päättelee, että alg funktiolla on tyyppi EitherF l r c -> c, joka on juuri sitä mitä tarvitset!
voit nyt nähdä, mihin kantotyyppi c on tarkoitettu. Se on tyyppi, jonka algebra poistaa, ja siten tyyppi, jonka katamorfismi palauttaa.
tämä on siis katamorfismi jommallekummalle. Kuten on ollut johdonmukainen toistaiseksi, se on pari, mutta nyt tehty kaksi toimintoa. Kuten olet toistuvasti nähnyt, tämä ei ole ainoa mahdollinen katamorfismi, sillä voit esimerkiksi triviaalisesti kääntää argumentit arvoon eitherF.
olen valinnut tässä esitetyn esityksen, koska se on isomorfinen either funktion kanssa Haskellin sisäänrakennetusta Data.Either-moduulista, joka kutsuu funktiota ”Either – tyypin Tapausanalyysiksi”. Molemmat näistä funktioista (eitherF ja either) vastaavat edellä mainittua C# Match – menetelmää.
Basis #
voit toteuttaa useimmat muut hyödylliset toiminnot eitherF. Tässä on Bifunctor instanssi:
instance Bifunctor EitherFix where bimap f s = eitherF (leftF . f) (rightF . s)
tästä instanssista Functor instanssi seuraa triviaalisesti:
instance Functor (EitherFix l) where fmap = second
päälle Functor voit lisätä Applicative:
instance Applicative (EitherFix l) where pure = rightF f <*> x = eitherF leftF (<$> x) f
ilmoitus, että <*> toteutus on samankaltainen kuin <*> toteutus MaybeFix. Sama pätee Monad esiintymään:
instance Monad (EitherFix l) where x >>= f = eitherF leftF f x
ei vain ole EitherFix Foldable, se on Bifoldable:
instance Bifoldable EitherFix where bifoldMap = eitherF
huomaa mielenkiintoista, että bifoldMap on sama kuin eitherF.
Bifoldable instanssi mahdollistaa Foldable instanssin triviaalisen toteutuksen:
instance Foldable (EitherFix l) where foldMap = bifoldMap mempty
mempty esiintyminen voi tuntua hämmentävältä, sillä bifoldMap (tai eitherF; ne ovat identtisiä) ottaa argumentteina kaksi funktiota. Onko mempty funktio?
Kyllä, mempty voi olla funktio. Tässä se on. On olemassa Monoid instanssi mille tahansa funktiolle a -> m, missä m on Monoid instanssi, ja mempty on kyseisen monoidin identiteetti. Se on tässä käytössä oleva esimerkki.
aivan kuten EitherFix on Bifoldable, on myös Bitraversable:
instance Bitraversable EitherFix where bitraverse fl fr = eitherF (fmap leftF . fl) (fmap rightF . fr)
Traversable instanssin voi toteuttaa mukavasti Bitraversable instanssin pohjalta:
instance Traversable (EitherFix l) where sequenceA = bisequenceA . first pure
lopuksi voidaan toteuttaa muunnoksia standardin Either tyypin kanssa, käyttäen ana duaalina cata:
toEither :: EitherFix l r -> Either l rtoEither = eitherF Left Right fromEither :: Either a b -> EitherFix a bfromEither = EitherFix . ana coalg where coalg (Left l) = LeftF l coalg (Right r) = RightF r
tämä osoittaa, että EitherFix on isomorfinen Either, mikä taas osoittaa, että eitherF ja either ovat ekvivalentteja.
suhteet #
tässä sarjassa on nähty useita esimerkkejä katamorfismeista rakenteissa, joissa ei ole poimuja, katamorfismeista, jotka yhtyvät poimuihin, ja nyt katamorfismista, joka on taitosta yleisempi. Sarjan johdanto sisälsi tämän kaavion:
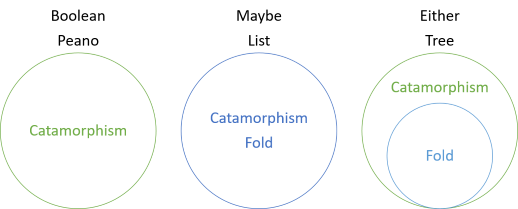
tämä osoittaa, että Boolen arvoilla ja Peanon luvuilla on katamorfismeja, mutta ei poimuja, kun taas Mayben ja Listin kohdalla taitos ja katamorfismi ovat samat. Kummallekaan taitos on kuitenkin katamorfismin erikoistapaus. Kansi joko ”teeskentelee”, että vasemmalla puolella ei ole olemassa. Sen sijaan vasen arvo tulkitaan puuttuvaksi oikeaksi arvoksi. Näin, jotta taita joko arvoja, sinun täytyy antaa ”fallback” arvo, jota käytetään, jos jompikumpi arvo ei ole oikea arvo:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e""
edellä mainitun kaltaisessa GHCi-istunnossa voit luoda kaksi samantyyppistä arvoa. Oikea tapaus on Ordering arvo, kun taas vasen tapaus on Integer arvo.
kun foldr, vasemmanpuoleiseen koteloon ei pääse käsiksi. Vaikka voit käyttää ja muuttaa oikeaa Ordering arvoa, numero 42 yksinkertaisesti ohitetaan taitoksen aikana. Sen sijaan palautetaan oletusarvo "".
vertaa tätä katamorfismiin, joka voi käyttää molempia tapauksia:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"42"
tällaisessa istunnossa luodaan samat arvot uudelleen, mutta käyttämällä katamorfismia eitherF voit nyt käyttää ja muuttaa sekä vasenta että oikeaa tapausta. Toisin sanoen, katamorfismin avulla voit suorittaa operaatioita, jotka eivät ole mahdollisia taitoksen kanssa.
on kuitenkin mielenkiintoista huomata, että vaikka taitos on katamorfismin erikoistuminen, bifold on identtinen katamorfismin kanssa.
Yhteenveto #
jommankumman katamorfismi on funktiopari. Yksi funktio muuttaa vasemman tapauksen, kun taas toinen funktio muuttaa oikean tapauksen. Kummallekin arvolle käytetään vain yhtä näistä funktioista.
kun alun perin törmäsin katamorfismin käsitteeseen, minun oli vaikea erottaa katamorfismia ja foldia toisistaan. Ongelmani oli, luulen, että tutorials törmäsin enimmäkseen käytetty linkitetty luettelot osoittaa, miten, siinä tapauksessa, kansi on katamorfismi. Kävi kuitenkin ilmi, että näin ei aina ole. Katamorfismi on yleinen abstraktio. Taitos taas tuntuu minusta liittyvän lähinnä kokoelmiin.
tässä artikkelissa näit ensimmäisen esimerkin katamorfismista, joka voi tehdä muutakin kuin taitoksen. Kummallekin taitos on vain katamorfismin erikoistapaus. Näit kuitenkin myös, miten katamorfismi oli identtinen bifoldin kanssa. Näin ollen ei ole vielä täysin selvää, miten nämä käsitteet liittyvät. Siksi seuraavassa artikkelissa, saat esimerkin säiliö, jossa ei ole bifold, ja jossa katamorfismi On, todellakin, yleistys taitoksen.
Seuraava: Puukatamorfismi.