tänään on lyhyt johdatus vuonna Pyöreä tilastot (joskus kutsutaan suuntaava tilastot). Circular statistics on mielenkiintoinen osa-alue tilastoja, joissa havainnot otetaan vektoreina ympäri yksikköympyrä. Kuvitelkaamme esimerkiksi, miten sairaalassa mitattaisiin syntymäaikoja 24 tunnin sykleissä tai miten muuttavien eläinten ryhmä hajaantuu. Tällaisia tietoja on mukana useilla eri aloilla, kuten ekologiassa, ilmastotieteessä ja biokemiassa. Mittahavaintojen luonne yksikköympyrän ympärillä edellyttää erilaista lähestymistapaa hypoteesitestaukseen. Jakaumat on” käärittävä ” ympyrän ympärille, jotta niistä olisi hyötyä, ja tavanomaiset estimaattorit, kuten näytteen keskiarvo tai näytteen varianssi, eivät sisällä vettä.
tässä viestissä teemme Rao: n Etäisyystestin, jolla arvioidaan pyöreän aineiston yhdenmukaisuutta. Tämä on perusmenettely, ja sitä tulisi pitää johdantona kiertotietojen käsittelyyn.
alku
teemme kilpikonnilla hypoteesitestin, joka on pieni aineisto, joka koostuu 10 vihermerikilpikonnan tulokulmista pesimäsaarelleen. Tavoitteenamme on selvittää, missä tulokulmissa näkyy suuntautumisen merkkejä tai ovat enemmän viitteellisiä satunnaiseen hajaantumiseen.
asenna ensin circular – paketti ja liitä mukaan turtles-tietokokonaisuus.
install.packages("circular")require(circular)attach(turtles)
tietojen piirtäminen
circularpaketti sisältää Oman piirtofunktion, plot.circular. Tarkkaillaan kilpikonnien tulokulmia.
plot.circular(arrival)
tässä on tontti: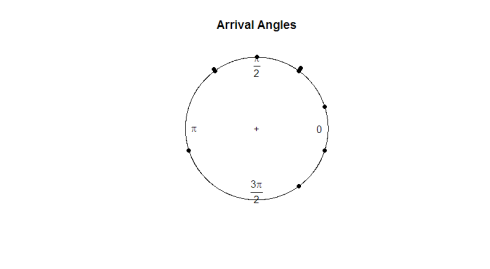
silmätestin perusteella havainnot näyttävät olevan yhtenäisiä ympyrän ympärillä. Jos haluamme suorittaa hypoteesi testi määrittää, jos tiedot ovat todella yhtenäinen, meidän täytyy kehittää testi tilastotieto, joka toimii kulmatietoja.
mikä on meille hyvä parametri hyödynnettäväksi? Otoskeskiarvon ottaminen ei kerro paljoakaan datan suunnasta (180 astetta ei ole hyödyllinen 2 asteen ja 358 asteen keskiarvo). Seuraavassa kuvaajassa havainnoidaan, miten otoksen keskiarvosta ei ole mitään hyötyä tietomme muodon tai leviämisen kuvaamisessa.
mean(arrival)plot.circular(mean(arrival)) 0.9120794
tässä on tontti: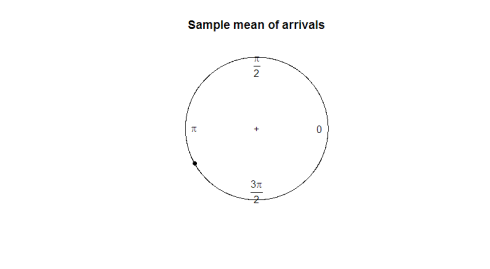
sen sijaan käytämme menetelmää, joka määrittää suunnan mittaamalla havaintojen välisen keskimääräisen tilan. Tätä testiä kutsutaan Raon Etäisyystestiksi.
Rao: n Etäisyystesti
RAO: n Etäisyystesti kehitettiin ympyräaineiston yhdenmukaisuuden arvioimiseksi. Se käyttää havaintojen välistä tilaa määrittääkseen, osoittaako data merkittävää suuntaavuutta. Jos tiedot ovat yhtenäisiä, havaintojen tulisi yleensä olla tasaisin välein.
tässä on RAO: n Etäisyystestin testitilasto \(U\): $$U = 1/2\sum\limits_{I=1}^n / T_{i} – λ| $$ missä \(λ = 360/n, T_{i} = f_{I+1} – f_{i}\) ja \(t_{n} = (360-f_{n})+f_{1}\)
periaatteessa testin tilastotiedot aggregoivat peräkkäisten pisteiden väliset poikkeamat, joista jokainen painotetaan aineistossa olevien havaintojen kokonaismäärällä.
käytämme rao.spacing.test() funktiota tämän hypoteesitestin suorittamiseen. Nollahypoteesimme mukaan data on tasajakaumaa, kun taas vaihtoehtoisissa osavaltioissa data osoittaa suuntautumisen merkkejä. Tehdään testi.
rao.spacing.test(arrival,alpha=.10) Rao's Spacing Test of Uniformity Test Statistic = 127.2689 Level 0.1 critical value = 161.23 Do not reject null hypothesis of uniformity
kun testin tilastollinen arvo 127 alittaa kriittisen arvon 161, tiedot eivät merkittävästi nojaa mihinkään suuntaan. Emme voi hylätä olettamusta, että Turtlesien saapuminen on jakautunut tasaisesti.
Conclusion
Rao: n etäisyystesti määritti, ettei aineistossa ollut merkkejä suuntaavista suuntauksista. Emme voi hylätä nollahypoteesia yhdenmukaisuudesta ja omaksumme yhdenmukaisuuden suhteen suuntaan saapua. Vaikka tämä viesti oli suhteellisen perus opetusohjelma, monet ihmiset data science yhteisössä eivät ole työskennelleet Pyöreä data ennen. Se on mielenkiintoinen subtooppinen sukeltaa sekä nuori tilastoala, joka kehittyy edelleen.
Loppuhuomautukset
haluaisin antaa tunnustusta S. Rao Jammalamadakalle, joka on PhD Kalifornian yliopistosta Santa Barbarasta, ja hänen oppikirjalleen ”Topics in Circular Statistics” siitä, että olen ollut kiinnostunut kiertotilastoista.