oletettu tietämys
opiskelijoilla on ollut laaja epävirallinen kokemus geometriasta aikaisempina vuosina, ja tämä antaa hyvän intuitiivisen perustan järjestelmällisemmälle lähestymistavalle geometriaan, joka soveltuu vuosille 7-10. Tämän moduulin kannalta merkityksellisiä aiheita vuosilta F−6 ovat:
- kompassien ja viivoittimien käyttö ja geometristen lukujen huolellinen piirtäminen.
- Kulmatyypit, mukaan lukien vähintään suorat kulmat, akuutit kulmat, tylppäkulmat ja
refleksikulmat. - kolmiot, mukaan lukien epävirallinen johdatus tasakylkisiin ja tasasivuisiin kolmioihin.
- Kvadrilateraalit, mukaan lukien epävirallinen johdatus neliöihin, suorakulmioihin, parallelogrammeihin, trapetseihin ja rhombuksiin.
- epävirallinen kokemus käännöksistä, heijastuksista, kiertoliikkeistä ja suurennoksista,
ja symmetrisesti esimerkiksi tasakylkisen kolmion, suorakulmion tai rhombuksen taittamisesta.
Motivaatio
 geometriaa käytetään meitä ympäröivän maailman mallintamiseen. Talojen katoista näkyy kolmioita, puolisuunnikkaita ja suorakulmioita, kun taas jalkakäytävien ja kylpyhuoneiden laatoituskuvioissa käytetään kuusikulmioita, viisikulmioita, kolmioita ja neliöitä.
geometriaa käytetään meitä ympäröivän maailman mallintamiseen. Talojen katoista näkyy kolmioita, puolisuunnikkaita ja suorakulmioita, kun taas jalkakäytävien ja kylpyhuoneiden laatoituskuvioissa käytetään kuusikulmioita, viisikulmioita, kolmioita ja neliöitä.
rakentajat, laatoittajat, arkkitehdit, Graafiset suunnittelijat ja verkkosuunnittelijat käyttävät rutiininomaisesti geometrisia ideoita työssään. Tällaisten geometristen kohteiden luokittelu ja niiden ominaisuuksien tutkiminen ovat erittäin tärkeitä. Geometrialla on myös monia sovelluksia taiteessa.
aivan kuten aritmetiikassa on numeroita sen peruskohteina, niin pisteet, viivat ja ympyrät ovat tasogeometrian perusrakenneosia.
lukiogeometriassa aloitetaan useilla intuitiivisilla ajatuksilla (pisteillä, viivoilla ja kulmilla), joita ei ole lainkaan helppo määritellä tarkasti, ja niiden jälkeen esitetään joitakin määritelmiä (vertikaalisesti vastakkaiset kulmat, yhdensuuntaiset viivat ja niin edelleen), joista päätellään tärkeitä tosiasioita, joita usein kutsutaan teoreemoiksi. Yläkoulussa kurinalaisuuden tason pitäisi kehittyä hitaasti vuodesta toiseen, mutta jokaisessa vaiheessa selkeä määrittely on erittäin tärkeää ja sitä on korostettava.
näin geometria antaa opiskelijoille mahdollisuuden kehittää geometrista intuitiotaan, jolla on sovelluksia monilla elämänalueilla, ja myös oppia rakentamaan loogisia argumentteja ja tekemään vähennyksiä asetelmassa, joka on suurimmaksi osaksi itsenäinen
luvusta.
sisältö
pisteet ja viivat
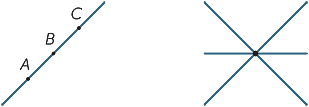
yksinkertaisimpia tasogeometriassa olevia kohteita ovat pisteet ja viivat. Koska ne ovat niin yksinkertaisia, on vaikea antaa tarkkoja määritelmiä niistä, joten sen sijaan pyrimme antamaan opiskelijoille karkean kuvauksen niiden ominaisuuksista, jotka ovat linjassa intuitiomme kanssa. Piste merkitsee paikkaa, mutta sillä ei ole kokoa. Käytännössä, kun piirrämme pisteen, sillä on selvästi selvä leveys, mutta se edustaa mielikuvituksessamme olevaa pistettä. Viivalla ei ole leveyttä ja se ulottuu äärettömästi molempiin suuntiin. Kun piirrämme viivan, sillä on leveys ja sillä on päät, joten se ei ole oikeastaan viiva, vaan edustaa viivaa mielikuvituksessamme. Koska kaksi erillistä pistettä A ja B sitten on yksi (ja vain yksi) linja, joka kulkee molempien pisteiden kautta. Isoilla kirjaimilla viitataan pisteisiin ja nimiriveihin joko ilmoittamalla kaksi pistettä suoralla tai käyttämällä pieniä kirjaimia, kuten  ja m. näin alla annettua riviä kutsutaan viivaksi AB tai viivaksi
ja m. näin alla annettua riviä kutsutaan viivaksi AB tai viivaksi  .
.

kun otetaan huomioon kaksi erillistä riviä, on olemassa kaksi mahdollisuutta: ne voivat joko kokoontua yhdessä pisteessä tai ne eivät koskaan kohtaa, riippumatta siitä, kuinka pitkälle niitä laajennetaan (tai tuotetaan). Viivoja, jotka eivät koskaan kohtaa, kutsutaan rinnakkaisiksi. Toisessa kaaviossa kirjoitetaan AB / / CD.
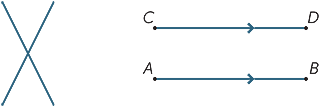
kolmea (tai useampaa) pistettä, jotka sijaitsevat suoralla, kutsutaan kollineaarisiksi.
kolmea (tai useampaa) Janaa, jotka kohtaavat yhdessä pisteessä, kutsutaan samanaikaisiksi.
|
|
|
| Kollineaari |
samanaikainen |
Harjoitus 1
piirrä kolme viivaa, jotka eivät ole yhtäaikaisia siten, ettei yhtäkään viivaa ole yhdensuuntaisia.
Harjoitus 2
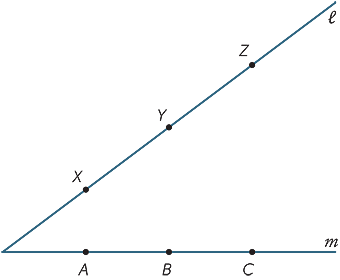
tee suuri kopio alla olevasta kaaviosta. Pisteet X, Y, Z ovat mitä tahansa pisteitä suoralla  ja A, B, C ovat mitä tahansa pisteitä suoralla m. liity ay ja XB kutsuvat leikkauspistettään R. liity BZ: ään ja YC: hen ja soita leikkauspistettään P. liity CX: ään ja ZA: han ja kutsu niiden leikkauspistettä Q. mitä huomaat pisteistä P, Q, R? (Tätä tulosta kutsutaan Pappuksen lauseeksi, N. 340 jKr.)
ja A, B, C ovat mitä tahansa pisteitä suoralla m. liity ay ja XB kutsuvat leikkauspistettään R. liity BZ: ään ja YC: hen ja soita leikkauspistettään P. liity CX: ään ja ZA: han ja kutsu niiden leikkauspistettä Q. mitä huomaat pisteistä P, Q, R? (Tätä tulosta kutsutaan Pappuksen lauseeksi, N. 340 jKr.)
intervallit, säteet ja kulmat
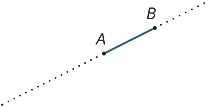 Oletetaan, että A ja B ovat kaksi pistettä suoralla. Väli
Oletetaan, että A ja B ovat kaksi pistettä suoralla. Väli
AB on a: n ja B: n välisen janan osa, mukaan lukien kaksi päätepistettä.
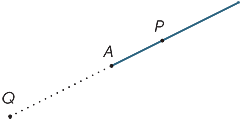 kaavion Kohta A jakaa janan kahteen osaan, joita kutsutaan säteiksi. Ray AP on, että ray, joka sisältää kohta P (ja Kohta A).
kaavion Kohta A jakaa janan kahteen osaan, joita kutsutaan säteiksi. Ray AP on, että ray, joka sisältää kohta P (ja Kohta A).
Kulmat
 kaaviossa säteiden OA ja OB välistä varjostettua aluetta kutsutaan kulmaksi AOB tai kulmaboaksi. Kulmamerkki
kaaviossa säteiden OA ja OB välistä varjostettua aluetta kutsutaan kulmaksi AOB tai kulmaboaksi. Kulmamerkki ![]() kirjoitetaan niin, että kirjoitetaan
kirjoitetaan niin, että kirjoitetaan ![]() AOB.
AOB.
 ulkona olevaa varjostettua aluetta kutsutaan OA: n ja OB: n muodostamaksi refleksikulmaksi. Suurimman osan ajasta, ellemme määrittele sanaa refleksi, kaikki kulmamme viittaavat säteiden väliseen alueeseen eivätkä niiden ulkopuolelle.
ulkona olevaa varjostettua aluetta kutsutaan OA: n ja OB: n muodostamaksi refleksikulmaksi. Suurimman osan ajasta, ellemme määrittele sanaa refleksi, kaikki kulmamme viittaavat säteiden väliseen alueeseen eivätkä niiden ulkopuolelle.
kulman koko
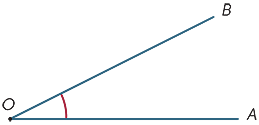 Kuvittele, että ray OB kiertää pisteen O ympäri, kunnes se sijaitsee OA: n varrella. Kääntymismäärää kutsutaan kulman AOB suuruudeksi. Voimme samalla tavalla määritellä refleksikulman koon.
Kuvittele, että ray OB kiertää pisteen O ympäri, kunnes se sijaitsee OA: n varrella. Kääntymismäärää kutsutaan kulman AOB suuruudeksi. Voimme samalla tavalla määritellä refleksikulman koon.
käytämme usein pieniä kreikkalaisia kirjaimia, α, β, γ,… edustamaan kulman kokoa.
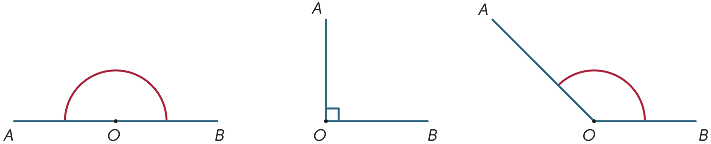
yhtä täyttä vallankumousta vastaavan kulman koko jaettiin (babylonialaisten toimesta) 360 yhtä suureen osaan, joita kutsumme asteiksi. (He luultavasti valitsivat 360, koska se oli lähellä päivien määrää vuodessa.) Näin ollen suoran kulman koko on 180° ja suoran kulman koko 90°. Muita kulmia voidaan mitata (likimäärin) astelevyllä.
|
|
||
| suora kulma | oikea kulma |
Tylppäkulma |
kulmat luokitellaan niiden koon mukaan. Sanomme, että kulma, jonka koko α on akuutti
(terävää tarkoittava sana), Jos 0° < α < 90°, α on tylppä (tylppää tarkoittava sana), jos
90° < α < 180° ja α on refleksi, jos 180° < α < 360°.
koska astelevyssä on kaksi asteikkoa, opiskelijan tulee olla tarkkana piirtäessään ja
mittauskulmia mitatessaan. On kannattavaa käyttää astelevyä piirtämään joitakin kulmia, kuten 30°, 78°, 130°, 163°.
Liikunta 3
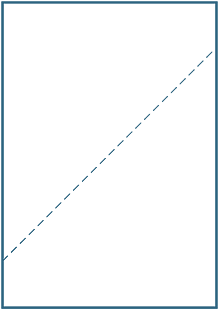 Taita A4-paperiarkki, joka vastaa (vinosti) vastakkaisia kulmia. Piirrä muodostuvaa prässia pitkin viiva ja mittaa prässin ja sivun väliset kulmat.
Taita A4-paperiarkki, joka vastaa (vinosti) vastakkaisia kulmia. Piirrä muodostuvaa prässia pitkin viiva ja mittaa prässin ja sivun väliset kulmat.
edellä esitetyssä harjoituksessa nämä kaksi kulmaa muodostavat yhdessä suoran ja lisäävät siten 180°: seen. Kahta kulmaa, jotka lisäävät 180°: een, kutsutaan täydentäviksi kulmiksi; siten 45° ja 135° ovat täydentäviä kulmia.
kahta kulmaa, jotka lisäävät 90°: een, kutsutaan komplementaarisiksi; näin 23° ja 67° ovat
komplementaariset kulmat.
kulmat pisteessä
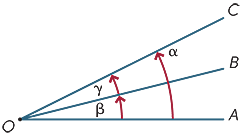 kaksi kulmaa pisteessä sanotaan vierekkäisiksi, jos niillä on yhteinen säde. Näin ollen kaaviossa
kaksi kulmaa pisteessä sanotaan vierekkäisiksi, jos niillä on yhteinen säde. Näin ollen kaaviossa ![]() AOB ja
AOB ja ![]() BOC ovat vierekkäisiä.
BOC ovat vierekkäisiä.
vierekkäiset kulmat voidaan lisätä, joten kaaviossa
α = β + γ.
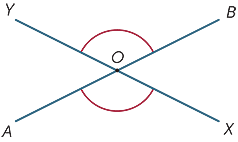
kun kaksi suoraa leikkaavat toisensa, muodostuu leikkauspisteeseen neljä kulmaa.
kaaviossa kulmia, jotka on merkitty ![]() AOX ja
AOX ja ![]() BOY, kutsutaan pystysuunnassa vastakkaisiksi.
BOY, kutsutaan pystysuunnassa vastakkaisiksi.
 lähtien
lähtien
-
 AOX on
AOX on  laatikon (suora kulma) täydennys.
laatikon (suora kulma) täydennys. -
 poika on myös
poika on myös  laatikon täydennys (suora kulma),
laatikon täydennys (suora kulma),
voimme päätellä, että nämä pystysuunnassa vastakkaiset kulmat, ![]() AOX ja
AOX ja ![]() BOY ovat yhtä suuret. Näin meillä on ensimmäinen
BOY ovat yhtä suuret. Näin meillä on ensimmäinen
tärkeä geometrinen lauseke:
pystysuunnassa vastakkaiset kulmat ovat yhtä suuret.
tulosta geometriassa (ja matematiikassa yleensä) kutsutaan usein lauseeksi. Lause on tärkeä lause, joka voidaan todistaa loogisella deduktiolla. Yllä oleva argumentti on todistus lauseelle; joskus todisteet esitetään muodollisesti lauseen toteamuksen jälkeen.
 jos kaksi Janaa leikkaavat toisensa niin, että kaikki neljä kulmaa ovat suorakulmaisia, sanotaan janojen olevan kohtisuorassa.
jos kaksi Janaa leikkaavat toisensa niin, että kaikki neljä kulmaa ovat suorakulmaisia, sanotaan janojen olevan kohtisuorassa.
kulmat pisteessä-geometriset argumentit
geometrisissa argumenteissa voidaan käyttää seuraavia syitä:
- vierekkäiset kulmat voidaan lisätä tai vähentää.
- kulmat vallankumouksessa lisäävät 360°: seen.
- kulmat suoralla lisätään 180°: seen.
- pystysuunnassa vastakkaiset kulmat ovat yhtä suuret.
poikittaiset ja yhdensuuntaiset linjat
 poikittainen on viiva, joka kohtaa kaksi muuta riviä.
poikittainen on viiva, joka kohtaa kaksi muuta riviä.
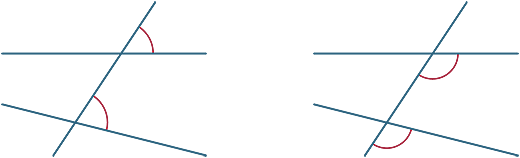
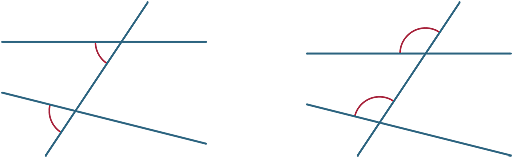
vastaavat kulmat
eri kulmat muodostuvat poikittain. Alla olevissa kaavioissa kahta merkittyä kulmaa kutsutaan vastaaviksi kulmiksi.
 nyt katsotaan, mitä tapahtuu, kun kaksi poikittaissuunnan katkaisemaa viivaa ovat yhdensuuntaisia.
nyt katsotaan, mitä tapahtuu, kun kaksi poikittaissuunnan katkaisemaa viivaa ovat yhdensuuntaisia.
Inituaalisesti, jos kulma α olisi suurempi kuin β, niin CD risteäisi AB: n F: n vasemmalle puolelle ja jos se olisi pienempi kuin β, se risteytyisi F: n oikealle puolelle.joten koska janat eivät ristiinny lainkaan, α ei voi olla pienempi eikä suurempi kuin β ja siten yhtä suuri kuin β.
vaihtoehtoisesti kuvitellaan kulman QGD kääntäminen GF: ää pitkin, kunnes g yhtyy F: n kanssa.koska janat ovat yhdensuuntaisia, oletamme kulman α yhtyvän kulman β kanssa. Tämä havainto johtaa meidät arveluihin, että:
vastaavat yhdensuuntaisista janoista muodostetut kulmat ovat yhtä suuret.
emme voi todistaa tätä tulosta, vaikka olemme osoittaneet, että se on geometrisesti uskottava. Hyväksymme sen geometrian aksioomana. Aksiooma on lausunto, jota emme voi todistaa, mutta joka on intuitiivisesti järkevä. Huomaa, että monet tosiasiat olemme jo todenneet, kuten: vierekkäiset kulmat voidaan lisätä, ja kaksi pistettä määrittää linjan jne., ovat myös aksioomia, vaikka emme ole nimenomaisesti ilmaisseet niitä tällä tavalla.
Vaihtoehtokulmia
kussakin kaaviossa kahta merkittyä kulmaa kutsutaan vaihtoehtokulmiksi (koska ne ovat poikittaissuunnan vaihtoehtoisilla sivuilla).

 jos suorat AB ja CD ovat yhdensuuntaisia, niin vaihtoehtoiset kulmat ovat yhtä suuret. Tämä tulos voidaan nyt todistaa.
jos suorat AB ja CD ovat yhdensuuntaisia, niin vaihtoehtoiset kulmat ovat yhtä suuret. Tämä tulos voidaan nyt todistaa.
![]() DGQ = α (vastaavat kulmat, AB / / CD)
DGQ = α (vastaavat kulmat, AB / / CD)
![]() DGQ = β (pystysuunnassa vastakkaiset kulmat G: ssä)
DGQ = β (pystysuunnassa vastakkaiset kulmat G: ssä)
joten α = β.
yhteenvetona:
rinnakkaisjanoista muodostetut Vaihtoehtoiset kulmat ovat yhtä suuret.
Co-sisäkulmat
lopuksi kussakin alla olevassa kaaviossa kahta merkittyä kulmaa kutsutaan co-sisäkulmiksi ja ne sijaitsevat poikittaisen samalla puolella.

jos janat AB ja CD ovat yhdensuuntaisia, niin on selvää, että yhdensuuntaiset kulmat eivät ole yhtä suuret, mutta osoittautuu, että ne ovat täydentäviä, eli niiden summa on 180° .
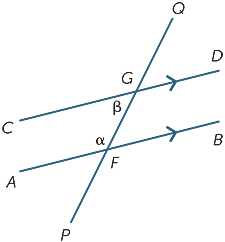 tämä on tulos, joka on myös helppo todistaa:
tämä on tulos, joka on myös helppo todistaa:
![]() BFG = β (vaihtoehtoiset kulmat, AB ||CD)
BFG = β (vaihtoehtoiset kulmat, AB ||CD)
α + β = 180° (suora kulma F: ssä)
yhteenvetona:
yhdensuuntaisista suorista muodostetut yhdensuuntaiset kulmat ovat täydentäviä.
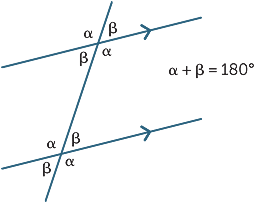 kolme tulosta voidaan tiivistää
kolme tulosta voidaan tiivistää
seuraavan kaavion avulla:
numeeriset esimerkit
kun otetaan huomioon tiedot kaavion kulmista, voidaan yllä olevien tulosten avulla selvittää kaavion muiden kulmien suuruus. Tämä on yksinkertainen, mutta erittäin tärkeä taito, jota usein kutsutaan epävirallisesti kulma jahtaaminen. Ongelmien ratkaisemisessa askeljärjestys ei ole aina ainutlaatuinen. Erilaisia, mutta yhtä päteviä lähestymistapoja voi olla useita.
esimerkiksi seuraavassa kaaviossa haetaan kulman BAC kokoa.

![]() DCA = 102° (vaihtoehtoiset kulmat, AC / BD)
DCA = 102° (vaihtoehtoiset kulmat, AC / BD)
![]() BAC = 78° (co-sisäkulma, AB / / CD)
BAC = 78° (co-sisäkulma, AB / / CD)
Harjoitus 4
käytä vaihtoehtoista vaiheiden sarjaa ![]() BAC: n löytämiseksi.
BAC: n löytämiseksi.
Liikunta 5
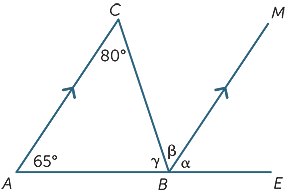 käyttäen vain yhdensuuntaisten janojen ominaisuuksia, Etsi (perusteluineen) puuttuvat kulmat seuraavasta kaaviosta.
käyttäen vain yhdensuuntaisten janojen ominaisuuksia, Etsi (perusteluineen) puuttuvat kulmat seuraavasta kaaviosta.
Harjoitus 6
Etsi α: n arvo seuraavasta kaaviosta.
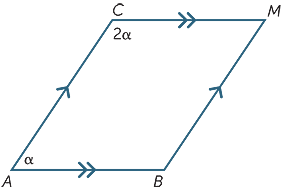
Käänteislauseet
monissa matematiikan väittämissä on käänteislause, jossa implisiittisyys menee päinvastaiseen suuntaan. Esimerkiksi lauseessa
” jokainen parillinen luku päättyy numeroon 0, 2, 4, 6 tai 8.”
on kääntynyt
” jokainen luku, joka päättyy 0: een, 2: een, 4: ään, 6: een tai 8: aan, on parillinen.”
tämä kyseinen lausuma ja sen kääntöpuoli ovat molemmat tosia, mutta näin ei suinkaan aina ole
.
esimerkiksi seuraavat kaksi lausetta ovat keskenään Converseja:
” jokainen 4: n kerrannainen on parillinen luku.”
” jokainen parillinen luku on 4: n kerrannainen.”
ja tässä ensimmäinen lausuma on tosi, mutta toinen on epätosi.
harjoitus 7
alaskirjaus:
a![]() tosi geometrinen lausunto, jonka käänteislause on myös tosi,
tosi geometrinen lausunto, jonka käänteislause on myös tosi,
b![]() väärä geometrinen lausunto, jonka käänteislause on tosi,
väärä geometrinen lausunto, jonka käänteislause on tosi,
c![]() väärä geometrinen lausunto, jonka käänteislause on myös epätosi.
väärä geometrinen lausunto, jonka käänteislause on myös epätosi.
yhdensuuntaisten suorien Käänteislauseet
olemme nähneet, että vastaavat yhdensuuntaisista suorista muodostetut kulmat ovat yhtä suuret. Voimme kirjoittaa converse lausuma seuraavasti.
lauseke: jos janat ovat yhdensuuntaiset, vastaavat kulmat ovat yhtä suuret.
Converse: Jos vastaavat kulmat ovat yhtä suuret, janat ovat yhdensuuntaiset.
myös käänteislause on tosi, ja sitä käytetään usein osoittamaan, että kaksi suoraa ovat yhdensuuntaisia. Sama pätee alternate – ja co-interior-kulmiin.
lauseke: jos janat ovat yhdensuuntaiset, niin vaihtoehtoiset kulmat ovat yhtä suuret.
Converse: jos vaihtoehtoiset kulmat ovat yhtä suuret,ovat janat yhdensuuntaiset.
lauseke: jos janat ovat yhdensuuntaisia, niin yhteissisäkulmat ovat täydentäviä.
Converse: Jos yhteissisäkulmat ovat täydentäviä, niin janat ovat yhdensuuntaisia.
näin ollen jokaisessa kaaviossa suorat AB ja CD ovat yhdensuuntaiset.

liikunta 8
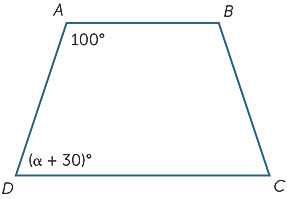 mikä α: n arvo tekee AB: stä samansuuntaisen CD: n kanssa?
mikä α: n arvo tekee AB: stä samansuuntaisen CD: n kanssa?
kolmen keskustelijan vedokset
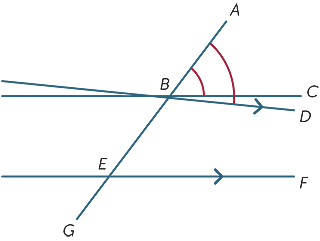 oletamme, että poikittaisten muodostamat vastaavat kulmat ovat yhtä suuret ja osoitamme, että janat ovat yhdensuuntaiset.
oletamme, että poikittaisten muodostamat vastaavat kulmat ovat yhtä suuret ja osoitamme, että janat ovat yhdensuuntaiset.
kaaviossa oletetaan, että ![]() ABC =
ABC = ![]() BEF.
BEF.
jos BC ja EF eivät ole yhdensuuntaisia, piirretään
BD yhdensuuntaisiksi EF: lle.
nyt kun BD ja EF ovat rinnakkaisia ![]() ABD =
ABD = ![]() BEF ja niin
BEF ja niin ![]() ABC =
ABC = ![]() ABD mikä on selvästi mahdotonta, elleivät suorat BC ja BD ole samat. Näin ollen linjat BC ja EF ovat yhdensuuntaisia.
ABD mikä on selvästi mahdotonta, elleivät suorat BC ja BD ole samat. Näin ollen linjat BC ja EF ovat yhdensuuntaisia.
muut vedokset seuraavat samalla tavalla.
harjoitus 9
antaa todisteen toisesta käänteislauseesta (vaihtoehtoisista kulmista).
kolmion kulmasumma
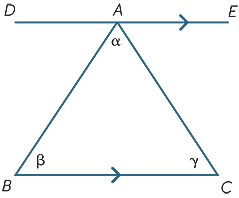 edellisen osion tuloksista voidaan päätellä yksi geometrian tärkeimmistä faktoista-kolmion kulmasumma on 180° .
edellisen osion tuloksista voidaan päätellä yksi geometrian tärkeimmistä faktoista-kolmion kulmasumma on 180° .
aloitetaan kolmion ABC kulmilla α, β, γ kuten on esitetty. Piirrä viiva dae rinnakkain BC. Sitten,
![]() DAB = β (vaihtoehtoiset kulmat, BC / / DE)
DAB = β (vaihtoehtoiset kulmat, BC / / DE)
![]() EAC = γ (vaihtoehtoiset kulmat, BC||DE)
EAC = γ (vaihtoehtoiset kulmat, BC||DE)
α+ β + γ = 180° (suora kulma).
näin olemme todistaneet lauseen
kolmion kulmien summa on 180°.
nelikulmio on tasoluku, jota rajoittaa neljä sivua.
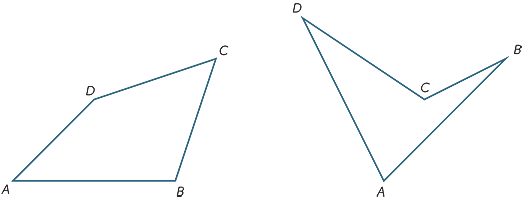
harjoitus 10
jakamalla nelikulmio ABCD kahteen kolmioon, etsitään kulmien summa.
linkit eteenpäin
tämän moduulin aineisto on alkanut sijoittaa geometrian kohtuullisen systemaattiselle perustalle tarkoin määriteltyjä objekteja, oletettavia aksioomia ja todistettuja teoreemoja. Tältä pohjalta voimme kehittää systemaattisen huomioon plane geometria, johon:
- Pythagoraan lause
- Kongruenssi ja kongruentit kolmiot
- samankaltaisuus ja vastaavat kolmiot
- tasakylkiset ja tasasivuiset kolmiot
- erityiset kvadrilateraalit, mukaan lukien neliöt, suorakulmiot, parallelogrammit, rhombukset ja trapezia
- geometria piireissä.
Tasogeometria on perustavaa laatua myös monilla muilla vuosien 7-10 matematiikan osa-alueilla:
- muunnokset
- Kolmiulotteinen geometria
- alueet ja tilavuudet
- Trigonometria
- koordinaattigeometria
- ympyröiden ja paraabelien kuvaajat.
tangenttien ja alueiden ajatukset johtavat vuorostaan laskemiseen vuosina 11-12.
historia ja soveltaminen
historia
Egyptin pyramidien ja valtavien temppelien uskomattomat rakennelmat paljastavat, että egyptiläisillä on täytynyt olla erittäin hyvä työskentelytaito ja ymmärrys perusgeometriasta ainakin käytännön tasolla. Toisaalta ei ole näyttöä siitä, että he olisivat systematisoineet tätä tietoa millään muodollisella tavalla. Tämä jäi antiikin kreikkalaisille. Meillä ei ole yksityiskohtaista tietoa tästä systematisoinnista, lukuun ottamatta väitettä, että Thales (n. 624 eaa. 546 eaa) antoi ensimmäisen ”vedoksia” geometrinen tosiasiat, jotka merkitsivät alkua deduktiivinen geometria. The Pythagoraan School jatkoi tätä työtä ja Platon (428 eaa -348 eaa) on selvästi hyödyntää työtä aiemmin matemaatikot, kun hän mainitsee geometrinen tosiasiat hänen kirjoituksia. Hänen teoksensa menon geometrinen dialogi, jossa Sokrates saa orjapojan päätymään geometriseen lauseeseen loogisten päätelmien avulla, on lukemisen arvoinen. Jos geometrian alkuperä on epäselvä, ”lopputuote” ei ole. Aleksandriassa kirjoittanut Eukleides (323-283 eaa.) laati merkittävän teoksen ”the Elements”, joka säilyi geometrian standardikirjana yli 2000 vuotta. Tässä työssä Eukleides esittää useita määritelmiä (kuten pistettä ja riviä), postulates, ja yhteisiä käsitteitä. (Nykyään kutsumme niitä aksioomiksi.) Näistä hän loogisesti kehitti hyvin huolellisesti valitussa järjestyksessä hyvin monta teoreemaa, joita yleensä kutsutaan Euklidiseksi Geometriaksi. On olemassa useita muitakin geometrisia tuloksia, kuten Pappuksen lause, jotka löydettiin Eukleideen jälkeen, mutta näitä ei yleensä käsitellä yläasteella.
yksi Eukleideen viidestä postulaatista ei ollut yhtä ilmeisen totta kuin muut näyttivät olevan. Yksi versio siitä, joka tunnetaan Playfairin Axiom todetaan, että: Koska viiva  ja piste P, ei
ja piste P, ei  , on olemassa yksi ja vain yksi rivi, joka on yhdensuuntainen
, on olemassa yksi ja vain yksi rivi, joka on yhdensuuntainen  , joka kulkee P: n kautta. 1800-luvulla joukko matemaatikkoja esitti kysymyksen ” Mitä tapahtuu, jos kiellämme tämän postulaatin?”Tämä tehdään olettamalla, että joko tällaista rinnakkaista viivaa ei ole, tai sanomalla, että tällaista viivaa on enemmän kuin yksi. Tämä johti epäeuklidisten geometrioiden kehittymiseen, joista yksi on osoittautunut yhdeksi maailmankaikkeuden hyvistä malleista.
, joka kulkee P: n kautta. 1800-luvulla joukko matemaatikkoja esitti kysymyksen ” Mitä tapahtuu, jos kiellämme tämän postulaatin?”Tämä tehdään olettamalla, että joko tällaista rinnakkaista viivaa ei ole, tai sanomalla, että tällaista viivaa on enemmän kuin yksi. Tämä johti epäeuklidisten geometrioiden kehittymiseen, joista yksi on osoittautunut yhdeksi maailmankaikkeuden hyvistä malleista.
Sovellukset
hyvin reaalisessa mielessä geometria ja geometrinen intuitio muodostavat kaikkien
matematiikan perustan − geometria johtaa koordinaattigeometriaan, joka johtaa laskutoimitukseen ja
kaikkiin sen moniin sovelluksiin − ja niin on ratkaisevaa opetussuunnitelmassa.
käytännöllisemmällä tasolla rakentajat, maanmittarit, insinöörit ja arkkitehdit ovat olleet geometrian ja geometristen ajatusten suurkuluttajia vuosisatojen ajan. Viime aikoina tietokoneiden kehityksen myötä graafikot ja web-suunnittelijat ovat liittyneet tähän ryhmään ihmisiä, jotka tarvitsevat ja käyttävät geometriaa työssään. Kun sovelletulta tiedemieheltä Jim Kellyltä kysyttiin äskettäin, miten hyödyllistä geometria on, hän sanoi:… geometria on tärkeä osa suunnittelua, piirtämistä ja tietokonemallinnusta. Sitä käytetään myös usein … fysiikka ja muut fysikaalisen tieteen kurssit osana ymmärrystä kuormien vaikutuksista rakenteisiin ja tasapainopisteisiin(painopisteisiin) komposiittikiinteistöille. Kemiassa molekyylin geometrian ymmärtäminen liittyy aineiden ominaisuuksien ymmärtämiseen. Esimerkkejä on paljon muitakin. (Ask a Scientist-sivustolta.)
Matematiikan historia: An Introduction, 3rd Edition, Victor J. Katz, Addison-Wesley, (2008)
History of Mathematics, D. E. Smith, Dover publications New York, (1958)
vastaukset harjoituksiin
harjoitus 1
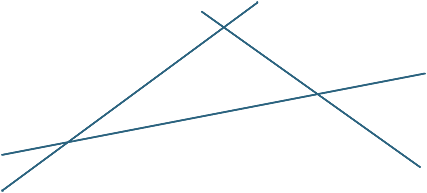
harjoitus 2
pisteet ovat kollineaarisia
harjoitus 3
60°
liikunta 4
![]() DBA = 102° (vastaavat kulmat, AB / / CD)
DBA = 102° (vastaavat kulmat, AB / / CD)
![]() BAC = 78° (co-interior angles, AC||BD)
BAC = 78° (co-interior angles, AC||BD)
EXERCISE 5
α = 65°![]() (vastaavat kulmat, AC||BM)
(vastaavat kulmat, AC||BM)
β = 80°![]() (vaihtoehtoiset kulmat, AC||BM)
(vaihtoehtoiset kulmat, AC||BM)
γ + β = 115°![]() (co-sisäkulmat, AC||BM)
(co-sisäkulmat, AC||BM)
siksi, γ = 35°
(tällä rakenteella todistetaan tulos, jonka mukaan kolmion kulmasumma on 180°)
Harjoitus 6
α = 60°
harjoitus 7
a![]() nelikulmio, jonka jokainen sisäkulma on suorakulmio.
nelikulmio, jonka jokainen sisäkulma on suorakulmio.
Converse: jokainen suorakulmion sisäkulma on oikea kulma.
b![]() suorakulmio on neliö
suorakulmio on neliö
Converse: neliö on suorakulmio
c![]() kolmion sisäkulmien kulmasumma on 200°
kolmion sisäkulmien kulmasumma on 200°
Converse: monikulmio, jonka sisäkulman summa on 200° on kolmio.
harjoitus 8
α = 50°
harjoitus 9
viittaamme samaan kaavioon.
aseta piste H suoralle EF E: n vasemmalle puolelle.
![]() CBE =
CBE = ![]() BEH
BEH
jos BC ja EF eivät ole yhdensuuntaisia, piirretään BD yhdensuuntaiseksi EF: lle.
koska BD ja EF ovat yhdensuuntaisia, ![]() EBD=
EBD= ![]() BEH, mikä on selvästi mahdotonta, elleivät janat BC ja BD ole samat.
BEH, mikä on selvästi mahdotonta, elleivät janat BC ja BD ole samat.
näin ollen janat BC ja EF ovat yhdensuuntaiset.
liikunta 10
360°
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 oli Australian hallituksen koulutus -, työllisyys-ja Työpaikkasuhteiden ministeriön rahoittama.
tässä esitetyt näkemykset ovat kirjoittajan näkemyksiä eivätkä välttämättä edusta Australian hallituksen koulutus -, työllisyys-ja Työpaikkasuhdeministeriön näkemyksiä.
© the University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (ellei toisin mainita). Tämä teos on lisensoitu Creative Commons Attribution – NonCommercial-NoDerivs 3.0 Unported-lisenssillä.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()