4.2 Estimoimalla lineaarisen regressiomallin kertoimia
käytännössä populaatioregressiolinjan leikkaus \(\beta_0\) ja kulmakerroin \(\beta_1\) ovat tuntemattomia. Siksi meidän on käytettävä tietoja arvioidaksemme molemmat tuntemattomat parametrit. Seuraavassa käytetään reaalimaailman esimerkkiä osoittamaan, miten tämä saavutetaan. Haluamme suhteuttaa koetulokset Kalifornian kouluissa mitattuihin oppilas-opettaja-suhdelukuihin. Koetulos on viidesluokkalaisten luku-ja matematiikkatulosten piirikeskiarvo. Luokkakoko mitataan jälleen oppilasmääränä jaettuna opettajien määrällä (oppilas-opettaja-suhde). Mitä tietoja, California School data set (CASchools) mukana R paketti nimeltään AER, lyhenne soveltavan Econometrics R (Kleiber and Zeileis 2020). Asennuksen jälkeen paketti asennus.paketit (”AER”) ja liittämällä se kirjastolla (AER) tietojoukko voidaan ladata funktiodatan () avulla.
## # install the AER package (once)## install.packages("AER")## ## # load the AER packagelibrary(AER)# load the the data set in the workspacedata(CASchools)kun paketti on asennettu, se on käytettävissä muissa yhteyksissä, kun sitä kutsutaan kirjastolla () — asennusta ei tarvitse suorittaa.paketteja () taas!
on mielenkiintoista tietää, millaisesta kohteesta on kyse.Luokka () palauttaa objektin luokan. Objektiluokasta riippuen jotkin funktiot (esimerkiksi juoni () ja yhteenveto ()) käyttäytyvät eri tavoin.
tarkastetaan olion Kaskoolien Luokka.
class(CASchools)#> "data.frame"on käynyt ilmi, että CASchools on luokan tietoja.kehys, joka on kätevä muoto työskennellä, erityisesti regressioanalyysin suorittamiseen.
pään() avulla saamme ensimmäisen yleiskuvan tiedoistamme. Tämä toiminto näyttää vain tietojoukon 6 ensimmäistä riviä, mikä estää ylikansoitetun konsolin ulostulon.
head(CASchools)#> district school county grades students teachers#> 1 75119 Sunol Glen Unified Alameda KK-08 195 10.90#> 2 61499 Manzanita Elementary Butte KK-08 240 11.15#> 3 61549 Thermalito Union Elementary Butte KK-08 1550 82.90#> 4 61457 Golden Feather Union Elementary Butte KK-08 243 14.00#> 5 61523 Palermo Union Elementary Butte KK-08 1335 71.50#> 6 62042 Burrel Union Elementary Fresno KK-08 137 6.40#> calworks lunch computer expenditure income english read math#> 1 0.5102 2.0408 67 6384.911 22.690001 0.000000 691.6 690.0#> 2 15.4167 47.9167 101 5099.381 9.824000 4.583333 660.5 661.9#> 3 55.0323 76.3226 169 5501.955 8.978000 30.000002 636.3 650.9#> 4 36.4754 77.0492 85 7101.831 8.978000 0.000000 651.9 643.5#> 5 33.1086 78.4270 171 5235.988 9.080333 13.857677 641.8 639.9#> 6 12.3188 86.9565 25 5580.147 10.415000 12.408759 605.7 605.4havaitsemme, että tietojoukko koostuu lukuisista muuttujista ja että useimmat niistä ovat numeerisia.
muuten: vaihtoehto luokalle() ja päähän() on str (), joka johdetaan ”rakenteesta” ja antaa kattavan yleiskuvan kohteesta. Yritä!
Palatakseni Kaskooleihin, kaksi muuttujaa, joista olemme kiinnostuneita (ts., keskiarvo kokeen pisteet ja opiskelija-opettaja suhde)eivät sisälly. Molemmat on kuitenkin mahdollista laskea annettujen tietojen perusteella. Opiskelija-Opettaja-suhdeluvun saamiseksi jaamme oppilasmäärän yksinkertaisesti opettajien määrällä. Testipistekeskiarvo on lukuarvosanan ja matematiikan kokeen pistemäärän aritmeettinen keskiarvo. Seuraava koodilohko näyttää, miten kaksi muuttujaa voidaan konstruoida vektoreiksi ja miten ne liitetään Caschooleihin.
# compute STR and append it to CASchoolsCASchools$STR <- CASchools$students/CASchools$teachers # compute TestScore and append it to CASchoolsCASchools$score <- (CASchools$read + CASchools$math)/2 jos ajoimme head (CASchools) uudelleen löytäisimme kaksi muuttujaa kiinnostaa ylimääräisiä sarakkeita nimeltä STR ja pisteet (tarkista tämä!).
oppikirjan taulukossa 4.1 on yhteenveto koetulosten jakaumasta sekä oppilas-opettaja-suhdeluvuista. On olemassa useita funktioita, joilla voidaan tuottaa samanlaisia tuloksia, esim.,
-
keskiarvo () (laskee annettujen lukujen aritmeettisen keskiarvon),
-
sd () (laskee otoksen keskihajonnan),
-
kvantiili () (Palauttaa määritetyn näytteen kvantiilien vektorin aineistolle).
seuraava koodinpätkä näyttää, miten tämä saavutetaan. Ensinnäkin laskemme Yhteenveto tilastoja sarakkeet STR ja pisteet CASchools. Saadaksemme hyvän tuotoksen keräämme toimenpiteet dataan.frame nimeltä DistributionSummary.
# compute sample averages of STR and scoreavg_STR <- mean(CASchools$STR) avg_score <- mean(CASchools$score)# compute sample standard deviations of STR and scoresd_STR <- sd(CASchools$STR) sd_score <- sd(CASchools$score)# set up a vector of percentiles and compute the quantiles quantiles <- c(0.10, 0.25, 0.4, 0.5, 0.6, 0.75, 0.9)quant_STR <- quantile(CASchools$STR, quantiles)quant_score <- quantile(CASchools$score, quantiles)# gather everything in a data.frame DistributionSummary <- data.frame(Average = c(avg_STR, avg_score), StandardDeviation = c(sd_STR, sd_score), quantile = rbind(quant_STR, quant_score))# print the summary to the consoleDistributionSummary#> Average StandardDeviation quantile.10. quantile.25. quantile.40.#> quant_STR 19.64043 1.891812 17.3486 18.58236 19.26618#> quant_score 654.15655 19.053347 630.3950 640.05000 649.06999#> quantile.50. quantile.60. quantile.75. quantile.90.#> quant_STR 19.72321 20.0783 20.87181 21.86741#> quant_score 654.45000 659.4000 666.66249 678.85999mitä näytteen tietoja, käytämme juoni (). Näin voimme havaita datamme ominaisuuksia, kuten poikkeamia, joita on vaikeampi löytää pelkillä numeroilla. Tällä kertaa lisätään joitakin lisäargumentteja juonenkutsuun().
ensimmäinen argumentti juonenkutsussamme (), pisteet ~ STR, on jälleen kaava, joka esittää muuttujat y – ja x-akselilla. Tällä kertaa muuttujia ei kuitenkaan tallenneta erillisiin vektoreihin, vaan ne ovat Kaskoolien sarakkeita. Siksi R ei löytäisi niitä ilman, että argumenttitiedot olisi määritetty oikein. tietojen on oltava tietojen nimen mukaisia.kehys, johon muuttujat kuuluvat, tässä tapauksessa CASchools. Lisäargumentteja käytetään tontin ulkonäön muuttamiseen: vaikka main lisää otsikon, xlab ja ylab lisäävät mukautettuja tarroja molempiin akseleihin.
plot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)")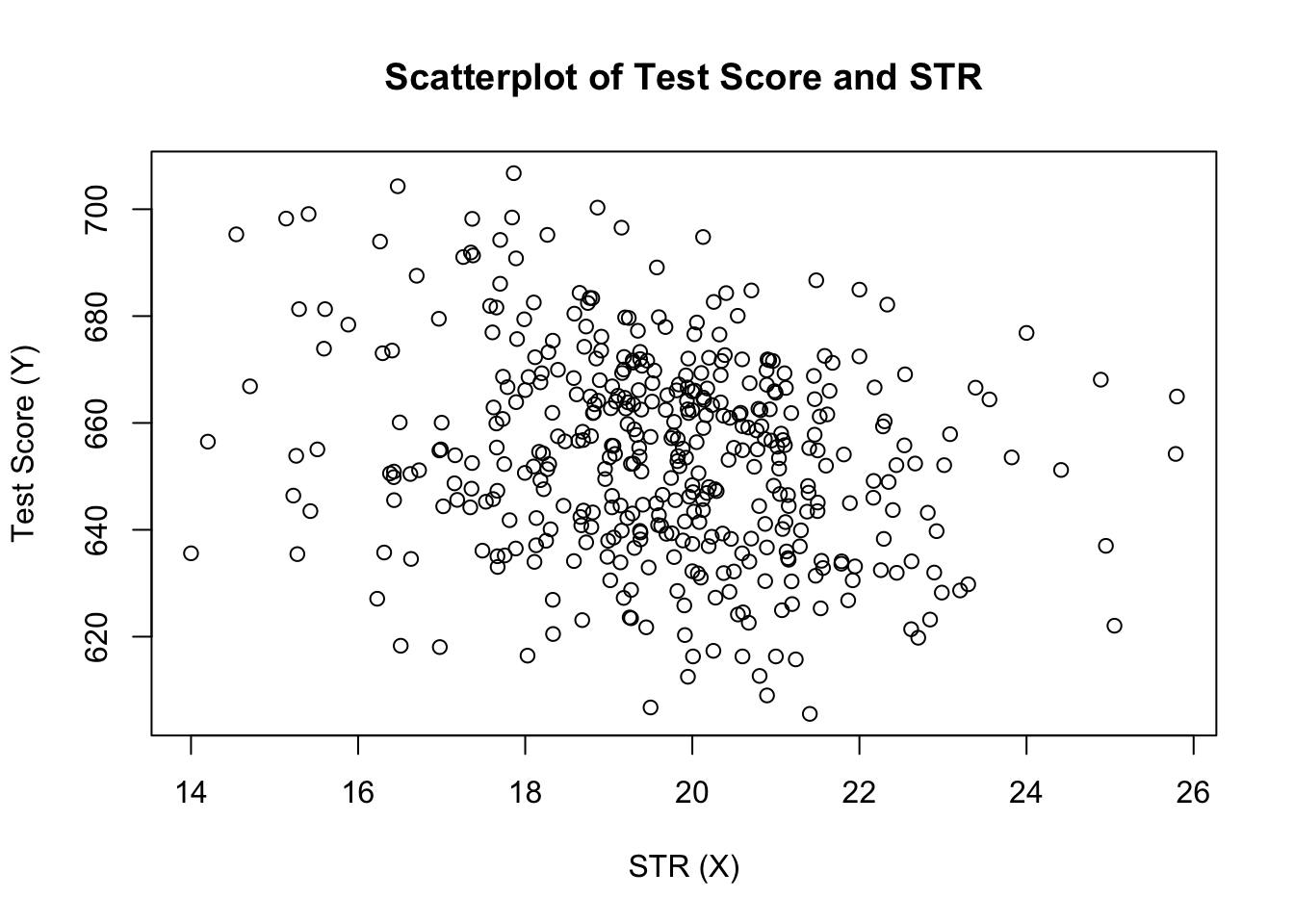
juoni (Kuva 4.2 kirjassa) näyttää kaikkien havaintojen scatterplot oppilas-opettaja suhde ja testi pisteet. Näemme, että pisteet ovat voimakkaasti hajallaan, ja että muuttujat korreloivat negatiivisesti. Toisin sanoen odotamme, että isommissa luokissa noudatetaan alhaisempia testituloksia.
funktio cor() (KS.cor lisätietoja) voidaan laskea korrelaatio kahden numeerinen vektori.
cor(CASchools$STR, CASchools$score)#> -0.2263627kuten scatterplot jo antaa ymmärtää, korrelaatio on negatiivinen, mutta melko heikko.
nyt tehtävänä on löytää dataan parhaiten sopiva rivi. Tietenkin voisimme yksinkertaisesti pitää kiinni graafisesta tarkastuksesta ja korrelaatioanalyysistä ja valita sitten silmäilemällä parhaan sovituslinjan. Tämä olisi kuitenkin melko subjektiivista: eri havainnoitsijat piirtäisivät erilaisia regressiorivoja. Tämän vuoksi olemme kiinnostuneita tekniikoista, jotka ovat vähemmän mielivaltaisia. Tällainen tekniikka saadaan tavallisen pienimmän neliösumman (OLS) estimoinnin avulla.
tavallinen pienimmän neliösumman estimaattori
OLS-estimaattori valitsee regressiokertoimet siten, että estimoitu regressiolinja on mahdollisimman ”lähellä” havaittuja datapisteitä. Tässä läheisyyttä mitataan \(Y\) annettujen \(X\) ennustamisessa tehtyjen neliövirheiden summalla. Olkoon \(b_0\) ja \(b_1\) joitakin \(\beta_0\) ja \(\beta_1\) estimaattoreita. Tällöin potenssiin laskettujen estimointivirheiden summa voidaan ilmaista seuraavasti
\
OLS-estimaattori yksinkertaisessa regressiomallissa on estimaattoripari sieppausta ja kaltevuutta varten, joka minimoi yllä olevan lausekkeen. OLS-estimaattorien derivointi molemmille parametreille esitetään kirjan lisäyksessä 4.1. Tulokset on koottu Avainkonseptiin 4.2.
OLS-estimaattori, ennustetut arvot ja jäännökset
yksinkertaisen lineaarisen regressiomallin OLS-estimaattorit \(\beta_1\) ja leikkaus \(\beta_0\) ovat\OLS-ennustetut arvot \(\widehat{Y}_i\) ja jäännökset \(\hat{u}_i\) ovat\
estimoitu leikkaus \(\hat{\beta}_0\), kaltevuusparametri \(\hat{\beta}_1\) ja jäännökset \(\Left(\Hat{U}_i\right)\) lasketaan otoksesta, jossa on \(n\) havaintoja \(x_i\) ja \(y_i\), \(i\), \(…\), \(ja\). Nämä ovat estimaatit tuntemattomasta perusjoukosta, jonka sieppaus on \(\left (\beta_0 \right)\), kaltevuus \(\left(\beta_1\right)\) ja virhetermi \((u_i)\).
edellä esitetyt kaavat eivät välttämättä ole kovin intuitiivisia ensisilmäyksellä. Seuraava interaktiivinen sovellus pyrkii auttamaan sinua ymmärtämään OLS: n mekaniikkaa. Havaintoja voi lisätä klikkaamalla koordinaattijärjestelmään, jossa tiedot esitetään pistein. Kun kaksi tai useampia havaintoja on saatavilla, sovellus laskee regressiolinjan käyttäen OLS: ää ja joitakin tilastoja, jotka näkyvät oikeassa paneelissa. Tulokset päivittyvät sitä mukaa, kun lisää havaintoja vasempaan paneeliin. Kaksoisnapsauta nollaa sovelluksen, eli kaikki tiedot poistetaan.
on monia mahdollisia tapoja laskea \(\Hat {\beta}_0\) ja \(\hat{\beta}_1\) R: ssä. voisimme esimerkiksi toteuttaa Avainkäsitteessä 4.2 esitetyt kaavat kahdella r: n perustoiminnolla: keskiarvo() ja summa(). Ennen tätä kiinnitämme CASchools-aineiston.
attach(CASchools) # allows to use the variables contained in CASchools directly# compute beta_1_hatbeta_1 <- sum((STR - mean(STR)) * (score - mean(score))) / sum((STR - mean(STR))^2)# compute beta_0_hatbeta_0 <- mean(score) - beta_1 * mean(STR)# print the results to the consolebeta_1#> -2.279808beta_0#> 698.9329Calling attach (CASchools) antaa meille mahdollisuuden käsitellä Caschoolsin sisältämää muuttujaa sen nimellä: ei ole enää tarpeen käyttää $ – operaattoria yhdessä tietokokonaisuuden kanssa: R voi arvioida muuttujan nimen suoraan.
r käyttää objektia käyttäjäympäristössä, jos tämä objekti jakaa oheisen tietokannan muuttujan nimen. On kuitenkin parempi tapa käyttää aina erottuvia nimiä tällaisten (näennäisesti) ristiriitaisuuksien välttämiseksi!
huomaa, että adress muuttujat sisältyvät liitteenä aineisto CASchools suoraan loput tästä luvusta!
näiden tehtävien suorittamiseen on toki vielä enemmän manuaalisia tapoja. Koska OLS on yksi yleisimmin käytetyistä estimointitekniikoista, R sisältää tietenkin jo sisäänrakennetun funktion nimeltä lm () (lineaarinen malli), jota voidaan käyttää regressioanalyysin tekemiseen.
määriteltävän funktion ensimmäinen argumentti on kuvaajan () tapaan regressiokaava, jonka perussyntaksi on y ~ X, jossa y on riippuvainen muuttuja ja x selittävä muuttuja. Argumenttitiedot määrittävät regressiossa käytettävän tietojoukon. Nyt palaamme kirjasta otettuun esimerkkiin, jossa analysoidaan testipisteiden ja luokkakokojen suhdetta. Seuraavassa koodissa käytetään lm: ää() toistamaan kirjan kuvassa 4.3 esitetyt tulokset.
# estimate the model and assign the result to linear_modellinear_model <- lm(score ~ STR, data = CASchools)# print the standard output of the estimated lm object to the console linear_model#> #> Call:#> lm(formula = score ~ STR, data = CASchools)#> #> Coefficients:#> (Intercept) STR #> 698.93 -2.28lisätään kuvioon arvioitu regressiolinja. Tällä kertaa laajennamme myös molempien akselien valikoimia asettamalla argumentit xlim ja ylim.
# plot the dataplot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)", xlim = c(10, 30), ylim = c(600, 720))# add the regression lineabline(linear_model) 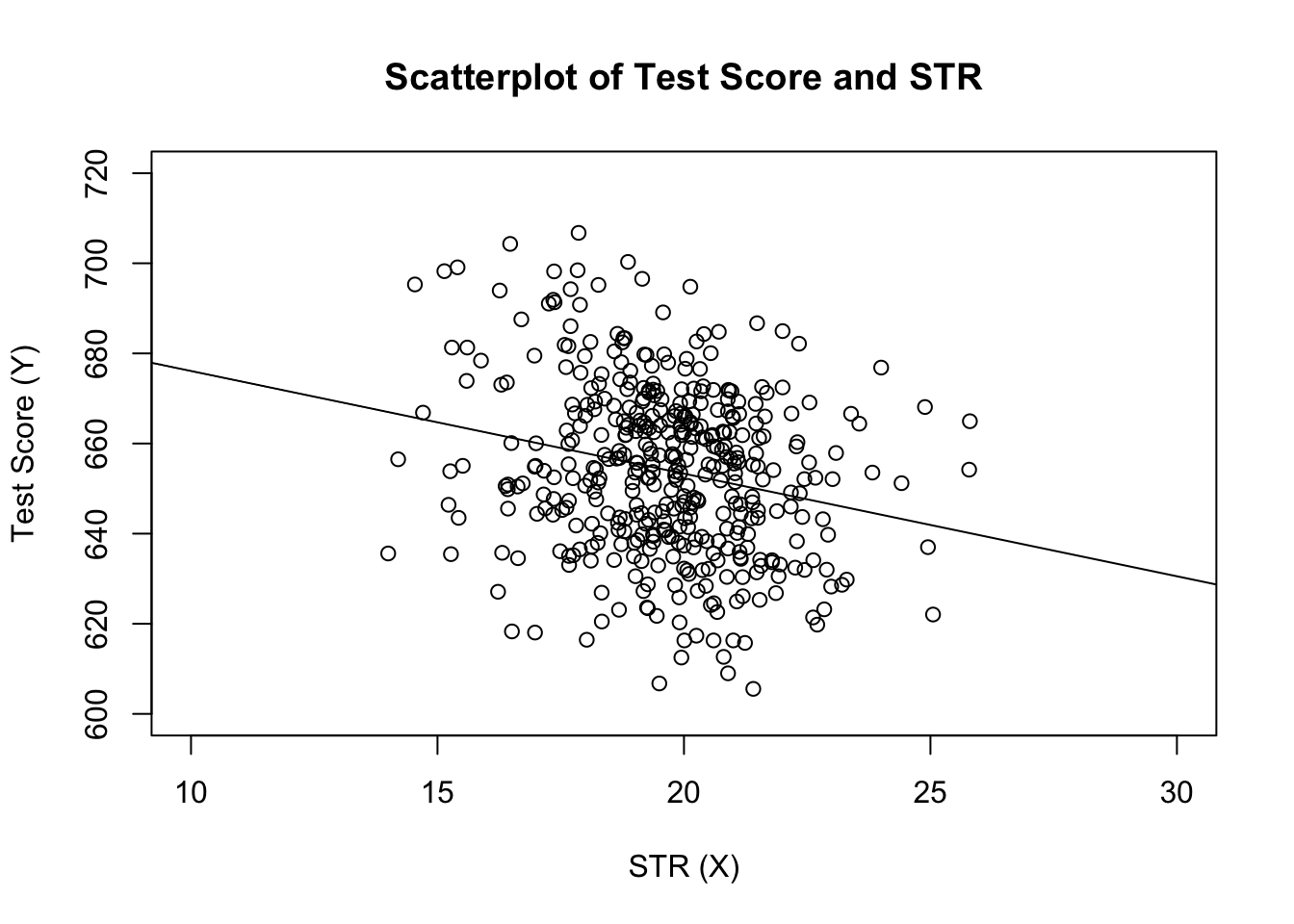
Huomasitko, että tällä kertaa emme siirtäneet sieppaus-ja kaltevuusparametreja ablinelle? Jos soitat abline () on objekti luokan lm joka sisältää vain yhden regressor, R piirtää regressioviivan automaattisesti!