Assessment | Biopsychology | Comparative |Cognitive | Developmental | Language | Individual differences |Personality | Philosophy | Social |
Methods | Statistics |Clinical | Educational | Industrial |Professional items |World psychology |
Statistics:Scientific method · Research methods · Experimental design · Undergraduate statistics courses · Statistical tests · Game theory · Decision theory
auta parantamaan tätä sivua itse, jos voit..
klusterianalyysi eli klusterointi on yleinen tilastotietojen analyysin tekniikka, jota käytetään monilla aloilla, kuten koneoppimisessa, tiedon louhinnassa, kuviotunnistuksessa, kuva-analyysissä ja bioinformatiikassa. Klusterointi on samankaltaisten kohteiden luokittelua eri ryhmiin, tai tarkemmin, tietojoukon jakautumista osajoukkoihin (klustereihin), niin että kunkin osajoukon tiedoilla (ihannetapauksessa) on jokin yhteinen piirre – usein läheisyys jonkin määritellyn etäisyysmittarin mukaan.
termin data clustering (tai vain clustering) lisäksi on olemassa useita termejä, joilla on samanlaisia merkityksiä, kuten klusterianalyysi, automaattinen luokittelu, numeerinen taksonomia, botryologia ja typologinen analyysi.
- Ryhmittelytyypit
- hierarkkinen ryhmittely
- Etäisyysmitta
- klustereiden luominen
- Agglomeratiivinen hierarkkinen ryhmittymä
- Partitional clustering
- k-means ja derivaatat
- K-means clustering
- QT Clust algorithm
- sumea c – tarkoittaa sumeassa ryhmittelyssä
- Kyynärkriteeri
- Spektriklusterointi
- Sovellukset
- biologia
- markkinointitutkimus
- muut sovellukset
- tietojen ryhmittelyjen vertailu
- Katso myös
- bibliografia
- Ohjelmistototeutukset
- Vapaa
Ryhmittelytyypit
tiedon ryhmittelyalgoritmit voivat olla hierarkkisia tai partitiivisia. Hierarkkiset algoritmit löytävät peräkkäiset klusterit käyttäen aiemmin luotuja klustereita, kun taas partiaaliset algoritmit määrittävät kaikki klusterit kerralla. Hierarkkiset algoritmit voivat olla agglomeratiivisia (alhaalta ylöspäin) tai jaollisia (ylhäältä alaspäin). Agglomeratiiviset algoritmit aloittavat jokaisesta alkuaineesta erillisenä klusterina ja yhdistävät ne peräkkäin suurempina klustereina. Jaolliset algoritmit alkavat koko joukosta ja etenevät jakamaan sen peräkkäin pienempiin klustereihin.
hierarkkinen ryhmittely
Etäisyysmitta
hierarkkisen ryhmittelyn keskeinen vaihe on valita etäisyysmitta. Yksinkertainen mitta on Manhattanin etäisyys, joka vastaa kunkin muuttujan absoluuttisten etäisyyksien summaa. Nimi tulee siitä, että kahden muuttujan tapauksessa muuttujat voidaan piirtää ruutukaavaan, jota voidaan verrata kaupungin katuihin, ja kahden pisteen välinen etäisyys on korttelien lukumäärä, jonka ihminen kävelisi.
yleisempi mitta on Euklidinen etäisyys, joka lasketaan löytämällä kunkin muuttujan välisen etäisyyden neliö, laskemalla yhteen neliöt ja löytämällä kyseisen summan neliöjuuri. Kaksimuuttujan tapauksessa etäisyys on analoginen hypotenuusan pituuden löytämisen kanssa kolmiossa; toisin sanoen se on etäisyys ”linnuntietä.”Terveyspsykologian tutkimuksen klusterianalyysin katsauksessa havaittiin, että yleisin etäisyysmitta julkaistuissa tutkimuksissa kyseisellä tutkimusalueella on Euklidinen etäisyys tai neliömäinen Euklidinen etäisyys.
klustereiden luominen
etäisyysmitan perusteella elementit voidaan yhdistää. Hierarkkinen ryhmittymä rakentaa (agglomeratiivista) eli hajottaa (jaollista) klusterien hierarkiaa. Tämän hierarkian perinteinen esitys on puun tietorakenne (jota kutsutaan dendrogrammiksi), jonka toisessa päässä on yksittäisiä alkuaineita ja toisessa yksi klusteri, jossa on kaikki alkuaineet. Agglomeratiiviset algoritmit alkavat puun latvasta, kun taas jaolliset algoritmit alkavat pohjasta. (Kuvassa nuolet osoittavat agglomeratiivista ryhmittymistä.)
puun leikkaaminen tietyllä korkeudella antaa ryhmittelyn valitulla tarkkuudella. Seuraavassa esimerkissä leikkaamalla toisen rivin jälkeen saadaan klustereita {a} {b c} {d e} {f}. Kolmannen rivin jälkeen leikkaaminen tuottaa klustereita {a} {b c} {d e f}, mikä on karkeampi klusterointi, jossa on vähemmän suurempia klustereita.
Agglomeratiivinen hierarkkinen ryhmittymä
Oletetaan esimerkiksi, että nämä tiedot on ryhmitelty. Missä euklidinen etäisyys on etäisyyden metriikka.
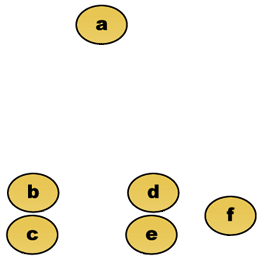
raakadata
hierarkkinen ryhmittely dendrogrammi olisi sellaisenaan:
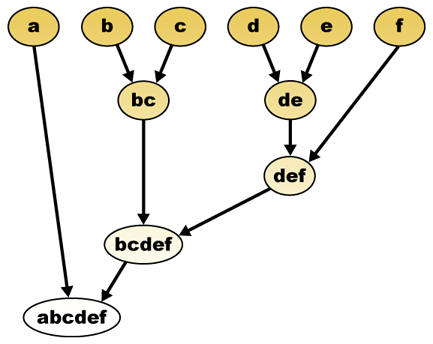
perinteinen edustus
tämä menetelmä rakentaa hierarkian yksittäisistä elementeistä yhdistämällä asteittain klustereita. Jälleen, meillä on kuusi elementtiä {a} {b} {c} {d} {e} ja {f}. Ensimmäinen vaihe on määrittää, mitkä elementit yhdistetään klusterissa. Yleensä haluamme ottaa kaksi lähintä alkiota, joten meidän on määriteltävä etäisyys 
Oletetaan, että olemme yhdistäneet kaksi lähintä alkiota b ja c, meillä on nyt seuraavat klusterit {a}, {b, c}, {d}, {e} ja {f}, ja haluamme yhdistää ne edelleen. Mutta tehdäksemme sen, meidän täytyy ottaa etäisyys {A} ja {b c}, ja siksi määritellä etäisyys kahden klusterin välillä. Yleensä kahden klusterin välinen etäisyys 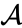
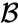
- kunkin klusterin elementtien välinen enimmäisetäisyys (kutsutaan myös täydelliseksi linkitysryhmittymäksi)):
- vähimmäisetäisyys elementtien välillä kunkin klusterin (kutsutaan myös single linkage clustering):
- kunkin klusterin elementtien välinen keskimääräinen etäisyys (kutsutaan myös keskimääräiseksi linkitysryhmittymäksi):
- kaikkien klusterin sisäisten varianssien summa
- yhteen sulautuvan klusterin varianssin kasvu (Wardin kriteeri)
- todennäköisyys, että kandidaattiklusterit kutevat samasta jakaumafunktiosta (V-linkage)
kukin taajama esiintyy suuremmalla etäisyydellä klustereiden välillä kuin edellinen taajama, ja voidaan päättää lopettaa klusterointi joko silloin, kun klusterit ovat liian kaukana toisistaan sulautuakseen (etäisyyskriteeri) tai kun klustereita on riittävän pieni määrä (lukumääräkriteeri).
Partitional clustering
k-means ja derivaatat
K-means clustering
K-means-algoritmi määrää jokaisen pisteen sille klusterille, jonka keskusta (jota kutsutaan myös centroidiksi) on lähin. Keskipiste on klusterin kaikkien pisteiden keskiarvo-toisin sanoen sen koordinaatit ovat aritmeettinen keskiarvo jokaiselle ulottuvuudelle erikseen kaikkien klusterin pisteiden osalta.
esimerkki: Tietojoukolla on kolme ulottuvuutta ja klusterilla on kaksi pistettä: X = (x1, x2, x3) ja Y = (y1, y2, y3). Tällöin centroidista Z tulee Z = (z1, z2, z3), jossa z1 = (x1 + y1)/2 ja z2 = (x2 + y2)/2 ja z3 = (x3 + y3)/2.
algoritmi on karkeasti (J. MacQueen, 1967):
- satunnaisesti tuottaa k klustereita ja määrittää klusterin keskukset, tai suoraan tuottaa k seed pistettä klusterin keskuksia.
- Määritä jokainen piste lähimpään klusterikeskukseen.
- Laske uudelleen Uudet klusterikeskukset.
- toistetaan, kunnes jokin konvergenssikriteeri täyttyy (yleensä tehtävä ei ole muuttunut).
tämän algoritmin tärkeimmät edut ovat sen yksinkertaisuus ja nopeus, jonka ansiosta sitä voidaan käyttää suurissa datajoukoissa. Sen haittana on, että se ei tuota samaa tulosta jokaisella suorituksella, koska tuloksena olevat klusterit riippuvat alustavista satunnaisista suorituksista. Se maksimoi klustereiden välisen (tai minimoi klusterin sisäisen) varianssin, mutta ei takaa, että tuloksella on globaali minimivarianssi.
QT Clust algorithm
QT (Quality Threshold) Clustering (Heyer et al, 1999) on vaihtoehtoinen menetelmä tietojen jakamiseen, joka on keksitty geeniklusterointia varten. Se vaatii enemmän laskentatehoa kuin K-keskiarvot, mutta ei vaadi klusterien lukumäärän määrittämistä ennalta, ja palauttaa aina saman tuloksen ajettaessa useita kertoja.
algoritmi on:
- käyttäjä valitsee klustereille maksimihalkaisijan.
- Rakenna kullekin pisteelle ehdokasklusteri sisällyttämällä siihen lähin piste, seuraavaksi lähin ja niin edelleen, kunnes klusterin halkaisija ylittää kynnyksen.
- Tallenna ehdokkaiden klusteri, jossa on eniten pisteitä, ensimmäiseksi todelliseksi klusteriksi ja poista kaikki klusterin pisteet jatkoharkinnasta.
- toistuu pelkistetyllä pistejoukolla.
pisteen ja pistejoukon välinen etäisyys lasketaan käyttäen täydellistä linkitystä, ts. koska suurin etäisyys pisteestä mihin tahansa ryhmän jäseneen (katso ”Agglomerative hierarchical clustering” – osio klusterien välisestä etäisyydestä).
sumea c – tarkoittaa sumeassa ryhmittelyssä
, että jokaisella pisteellä on sumean logiikan tapaan tietty kuulumisaste klustereihin sen sijaan, että se kuuluisi kokonaan vain yhteen klusteriin. Näin ollen klusterin reunalla olevat pisteet voivat olla klusterissa vähäisemmässä määrin kuin klusterin keskellä olevat pisteet. Jokaiselle pisteelle x meillä on Kerroin, joka antaa KTH: n tähtijoukon olemisen asteen 

sumealla C-keskiarvolla klusterin keskipiste on kaikkien pisteiden keskiarvo painotettuna niiden kuulumisasteella:
kuulumisaste on verrannollinen joukon etäisyyden käänteisarvoon
tällöin kertoimet normalisoidaan ja fuzzifioidaan reaaliparametrilla 
jos m on 2, Tämä vastaa kertoimen normalisointia lineaarisesti, jolloin niiden summa on 1. Kun m on lähellä 1, niin cluster center lähimpänä pistettä annetaan paljon enemmän painoa kuin muut, ja algoritmi on samanlainen k-means.
sumea c-means-algoritmi on hyvin samankaltainen k-means-algoritmin kanssa:
- Valitse useita klustereita.
- antaa satunnaisesti kullekin pistekertoimelle klustereissa olemisen.
- toistetaan, kunnes algoritmi on konvergoitunut (eli kertoimien muutos kahden iteraation välillä on enintään
, annettu herkkyyskynnys) :
- lasketaan kunkin klusterin centroid käyttäen yllä olevaa kaavaa.
- laske kullekin pisteelle Sen kertoimet siitä, että ne ovat klustereissa, käyttäen yllä olevaa kaavaa.
algoritmi minimoi myös klusterin sisäisen varianssin, mutta sillä on samat ongelmat kuin k-keskiarvoilla, minimi on paikallinen minimi ja tulokset riippuvat alkupainojen valinnasta.
Kyynärkriteeri
kyynärkriteeri on yleinen nyrkkisääntö, jolla määritetään, kuinka monta klusteria valitaan, esimerkiksi K-keskiarvoille ja agglomeratiiviselle hierarkkiselle ryhmittelylle.
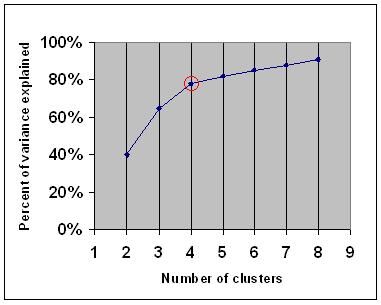
kyynärpääkriteeri sanoo, että kannattaa valita joukko klustereita, jotta toisen klusterin lisääminen ei tuo riittävästi tietoa. Tarkemmin sanottuna, jos kuvaat klustereiden selittämän varianssin prosenttiosuuden klustereiden lukumäärää vastaan, ensimmäiset klusterit lisäävät paljon tietoa (selittävät paljon varianssia), mutta jossain vaiheessa marginaalinen voitto laskee, jolloin kuvaajassa on kulma (kyynärpää).
Seuraavassa kuvaajassa kyynärpää on merkitty punaisella ympyrällä. Valittujen klusterien määrän tulisi siis olla 4.
Spektriklusterointi
kun otetaan huomioon tietopisteiden joukko, samankaltaisuusmatriisi voidaan määritellä matriisiksi 


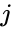
yksi tällainen tekniikka on Shi-Malikin algoritmi, jota käytetään yleisesti kuvien segmentointiin. Se jakaa pisteet kahdeksi joukoksi 


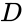
tämä jako voidaan tehdä eri tavoin, kuten ottamalla mediaani 



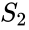
siihen liittyvä algoritmi on Meila-Shi-algoritmi, joka ottaa matriisin k suurimpia eigenvaluja vastaavat eigenvektorit 
Sovellukset
biologia
biologiassa ryhmittelyllä on monia sovelluksia laskennallisen biologian ja bioinformatiikan aloilla, joista kaksi on:
- transkriptomiikassa ryhmittelyä käytetään sellaisten geeniryhmien muodostamiseen, joilla on toisiinsa liittyviä ilmentymämalleja. Usein tällaiset ryhmät sisältävät toiminnallisesti toisiinsa liittyviä proteiineja, kuten tietyn reitin entsyymejä tai geenejä, jotka ovat yhteissäädeltyjä. Suuren suoritustehon kokeet, joissa käytetään expressed sequence tageja (ESTs) tai DNA-mikrorakenteita, voivat olla tehokas väline genomin merkinnässä, joka on genomiikan yleinen näkökohta.
- sekvenssianalyysissä ryhmitellään homologisia sekvenssejä geeniperheiksi. Tämä on erittäin tärkeä käsite bioinformatiikassa ja evoluutiobiologiassa yleensä. Katso evolution by geeni kahdentaminen.
markkinointitutkimus
Klusterianalyysiä käytetään laajalti markkinatutkimuksessa, kun käytetään kyselyjen ja testipaneelien monimuuttujatietoja. Markkinatutkijat käyttävät klusterianalyysiä jakaakseen yleisen kuluttajaväestön markkinasegmentteihin ja ymmärtääkseen paremmin eri kuluttajaryhmien/potentiaalisten asiakkaiden välisiä suhteita.
- Markkinasegmentointi ja kohdemarkkinoiden määrittäminen
- tuotesijoittelu
- Uusi tuotekehitys
- testimarkkinoiden valinta (KS . : kokeelliset tekniikat)
muut sovellukset
sosiaalinen verkostoanalyysi: sosiaalisten verkostojen tutkimuksessa voidaan käyttää ryhmittelyä suurten ihmisryhmien yhteisöjen tunnistamiseen.
Kuvan segmentointi: ryhmittelyllä voidaan jakaa digitaalinen kuva erillisiin alueisiin rajantunnistusta tai objektintunnistusta varten.
tiedonlouhinta: monissa tiedonlouhintasovelluksissa tietoalkiot jaetaan toisiinsa liittyviin osajoukkoihin; edellä käsitellyt markkinointisovellukset ovat joitakin esimerkkejä. Toinen yleinen sovellus on dokumenttien, kuten World Wide Web-sivujen, jakaminen genreihin.
tietojen ryhmittelyjen vertailu
on esitetty useita ehdotuksia kahden ryhmittelyn samankaltaisuuden mittaamiseksi. Tällaista mittaria voidaan käyttää vertailemaan, kuinka hyvin eri dataklusterointialgoritmit suoriutuvat tietomäärästä. Monet näistä mittauksista johdetaan vastaavuusmatriisista (eli sekaannusmatriisista), esimerkiksi Randin mitta ja Fowlkes-Mallows Bk-mitta.
- Jain, Murty and Flynn: Data Clustering: a Review, ACM Comp. Surv., 1999. Saatavilla täältä.
- toisessa esityksessä hierarkkiset, K-ja sumeat c-keinot, KS.tämä johdatus ryhmittelyyn. On myös selitys sekoitus Gaussilaiset.
- David Dowe, Sekoitusmallinnussivu-muut ryhmittelyt ja sekoitusmallilinkit.
- a tutorial on clustering
- The On-line textbook: Information Theory, Inference, and Learning Algorithms, by David J. C. MacKay sisältää lukuja k-means clustering, soft k-means clustering, ja derivations including the E-M algorithm and the variational view of the e-m algorithm.
Katso myös
- k-means
- keinotekoinen neuroverkko (ANN)
- itseorganisoituva kartta
- odotuksen maksimointi (EM)
bibliografia
- Clatworthy, J., Buick, D., Hankins, M., Weinman, J., & Horne, R. (2005). The use and reporting of cluster analysis in health psychology: A review. British Journal of Health Psychology 10: 329-358.
- Romesburg, H. Clarles, Cluster Analysis for Researchers, 2004, 340 s. ISBN 1411606175 tai kustantaja, uusintapainos Krieger pubin julkaisemasta vuoden 1990 painoksesta. Co… Japaninkielinen käännös on saatavilla Uchida Rokakuho Publishing Co., Ltd., Tokio, Japani.
- Heyer, L. J., Kruglyak, S. and Yooseph, S., Exploring Expression Data: Identification and Analysis of Coexpressed Genes, Genome Research 9: 1106-1115.
- David J. C. Mackayn on-line textbook: Information Theory, Inference, and Learning Algorithms sisältää lukuja k-means clustering, soft k-means clustering, ja johdannaisia, mukaan lukien E-M-algoritmi ja variational view of the E-M algorithm.
spektriklusterointiin :
- Jianbo Shi and Jitendra Malik, ”Normalized Cuts and Image segregation”, IEEE Transactions on Pattern Analysis and Machine Intelligence, 22 (8), 888-905, August 2000. Luettavissa Jitendra Malikin kotisivuilla
- Marina Meila and Jianbo Shi, ”Learning segregation with Random Walk”, Neural Information Processing Systems, NIPS, 2001. Saatavilla jianbo Shin kotisivuilta
klusterien lukumäärän arvioimiseksi:
- Can, F., Ozkarahan, E. A. (1990) ” Concepts and effectivity of the cover coefficient-based clustering methodology for text databases.”ACM-tapahtumat tietokantajärjestelmissä. 15 (4) 483-517.
Ohjelmistototeutukset
Vapaa
- flexclust-paketti R
- YALE (Yet Another Learning Environment): ilmainen avoimen lähdekoodin ohjelmisto tiedon löytämiseen ja tiedon louhintaan myös lisäosa ryhmittelyyn
- jotkut Matlab – lähdekooditiedostot ryhmittelyyn täällä
- kompakti vertailupaketti ryhmittelyarviointia varten (myös matlabissa)
- mixmod : Mallipohjainen Klusteri-Ja Diskriminanttianalyysi. Koodi C++, käyttöliittymä Matlabin ja Scilabin kanssa
- LingPipe Clustering opetusohjelma täydellisen ja yhden linkin clusteroinnin tekemiseen lingpipe-ohjelmalla, Java-tekstitietolouhintapaketilla, joka on jaettu Sourcen kanssa.
- Weka: Weka sisältää työkaluja tietojen esikäsittelyyn, luokitteluun, regressioon, ryhmittelyyn, assosiaatiosääntöihin ja visualisointiin. Se soveltuu hyvin myös uusien koneoppimisjärjestelmien kehittämiseen.