Noam Chomoskyn mukaan kielioppeja on neljää tyyppiä − tyyppi 0, Tyyppi 1, tyyppi 2 ja tyyppi 3. Seuraavassa taulukossa on esitetty, miten ne eroavat toisistaan−
| Kielioppityyppi | Grammar Accepted | Language Accepted | Automaton |
|---|---|---|---|
| Tyyppi 0 | rajoittamaton kielioppi | rekursiivisesti luettava kieli | Turingin kone |
| tyyppi 1 | Konteksti-herkkä kielioppi | Konteksti-herkkä kieli | Lineaarinen-rajattu Automaatti |
| tyyppi 2 | Kontekstiton kielioppi | Kontekstiton kieli | Pushdown automaton |
| tyyppi 3 | säännöllinen kielioppi | säännöllinen kieli | äärellinen valtionautomaatti |
katsohan seuraavaa kuvausta. Se osoittaa kunkin kielioppityypin laajuuden –
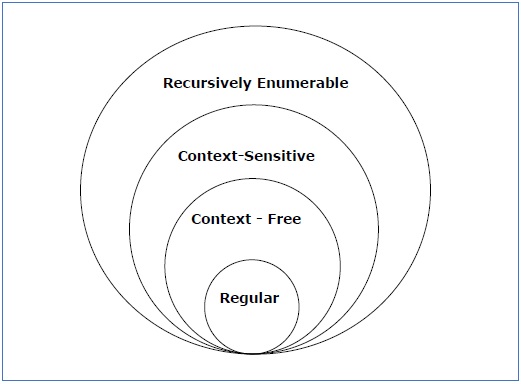
Type – 3-kielioppi
Type-3-kielioppi luo säännöllisiä kieliä. Tyypin 3 kielioppien vasemmalla puolella on oltava yksi pääte, joka ei ole pääte, ja oikealla puolella on oltava yksi pääte tai yksi pääte, jota seuraa yksi pääte, joka ei ole pääte.
produktioiden tulee olla muotoa X → A tai X → aY
missä X, Y ∈ n (ei pääte)
ja A ∈ T (pääte)
sääntö s → ε sallitaan, jos S ei esiinny minkään säännön oikealla puolella.
esimerkki
X → ε X → a | aYY → b
Type-2-kielioppi
Type-2-kielioppi luo kontekstivapaita kieliä.
produktioiden tulee olla muodossa a → γ
, jossa A ∈ n (muu kuin pääte)
ja γ ∈ (T ∪ n)* (päätteiden ja muiden kuin päätelaitteiden jono).
nämä näistä kielioireista syntyneet kielet tunnistetaan ei-deterministisellä työntöautomaatilla.
esimerkki
S → X a X → a X → aX X → abc X → ε
tyypin 1 kielioppi
tyypin 1 kieliopit luovat kontekstisensitiivisiä kieliä. Produktioiden tulee olla muotoa
α A β → α γ β
jossa A ∈ n (ei-terminaalinen)
ja α, β, γ ∈ (T ∪ n)* (päätteiden ja muiden kuin päätteiden merkkijonot)
merkkijonot α ja β voivat olla tyhjiä, mutta γ: n ei-tyhjiä.
sääntö s → ε sallitaan, jos S ei esiinny minkään säännön oikealla puolella. Näiden kielioppien tuottamat kielet tunnistetaan lineaarisella rajausautomaatilla.
esimerkki
AB → AbBc A → bcA B → b
Type – 0-kielioppi
Type-0-kielioppi luo rekursiivisesti lueteltavia kieliä. Tuotannoilla ei ole rajoituksia. Ne ovat mitä tahansa faasirakenteen kielioppia, mukaan lukien kaikki muodolliset kieliopit.
ne tuottavat Turingin koneen tunnistamat kielet.
produktiot voivat olla muodossa α → β, jossa α on jono päätteitä ja ei-terminaaleja, joissa on vähintään yksi ei-terminaali, eikä α voi olla nolla. β on jono päätteitä ja ei-päätteitä.
Esimerkki
S → ACaB Bc → acB CB → DB aD → Db