¿Qué es el Análisis de Clúster?
El análisis de clústeres es un análisis exploratorio que intenta identificar estructuras dentro de los datos. El análisis de clústeres también se denomina análisis de segmentación o análisis de taxonomía. Más específicamente, trata de identificar grupos homogéneos de casos si el agrupamiento no se conoce previamente. Debido a que es exploratoria, no hace distinción alguna entre variables dependientes e independientes. Los diferentes métodos de análisis de clústeres que ofrece SPSS pueden manejar datos binarios, nominales, ordinales y de escala (intervalo o relación).
El análisis de conglomerados se utiliza a menudo junto con otros análisis (como el análisis discriminante). El investigador debe ser capaz de interpretar el análisis de conglomerados en función de su comprensión de los datos para determinar si los resultados producidos por el análisis son realmente significativos.
Preguntas típicas de investigación las respuestas del análisis de clústeres son las siguientes:
- Medicina – ¿Cuáles son los grupos de diagnóstico? Para responder a esta pregunta, el investigador diseñaría un cuestionario de diagnóstico que incluye posibles síntomas (por ejemplo, en psicología, ansiedad, depresión, etc.).). El análisis de conglomerados puede luego identificar grupos de pacientes que tienen síntomas similares.
- Marketing – ¿Cuáles son los segmentos de clientes? Para responder a esta pregunta, un investigador de mercado puede realizar una encuesta que cubra las necesidades, las actitudes, la demografía y el comportamiento de los clientes. A continuación, el investigador puede utilizar el análisis de conglomerados para identificar grupos homogéneos de clientes que tienen necesidades y actitudes similares.
- Educación – ¿Cuáles son los grupos de estudiantes que necesitan atención especial? Los investigadores pueden medir las características psicológicas,de aptitud y de logro. A continuación, un análisis de conglomerados puede identificar qué grupos homogéneos existen entre los estudiantes (por ejemplo, alumnos de alto rendimiento en todas las asignaturas, o estudiantes que sobresalen en ciertas asignaturas pero fracasan en otras).
- Biología – ¿Qué es la taxonomía de las especies? Los investigadores pueden recopilar un conjunto de datos de diferentes plantas y anotar diferentes atributos de sus fenotipos. Un análisis de conglomerados puede agrupar esas observaciones en una serie de conglomerados y ayudar a construir una taxonomía de grupos y subgrupos de plantas similares.
Otras técnicas que puede probar para identificar grupos similares de observaciones son el análisis Q, el escalado multidimensional (MDS) y el análisis de clases latentes.
El Análisis de clústeres en SPSS
Nuestra pregunta de investigación para este ejemplo de análisis de clústeres es la siguiente:
¿Qué grupos homogéneos de estudiantes emergen en función de los resultados de exámenes estandarizados en matemáticas, lectura y escritura?
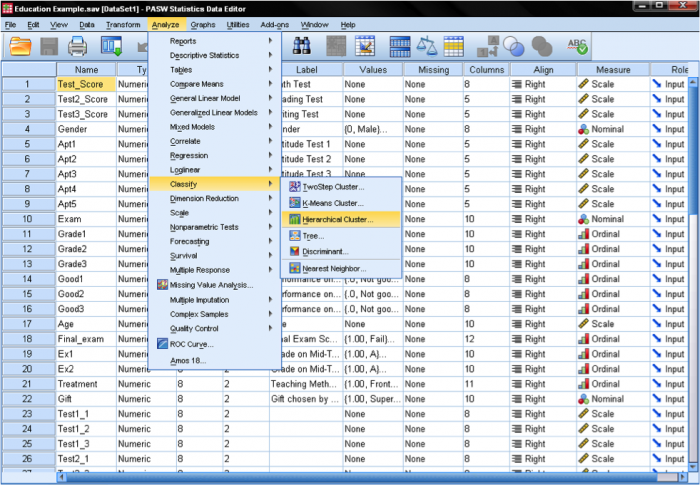
En SPSS, los análisis de clústeres se pueden encontrar en Analizar / Clasificar…. SPSS ofrece tres métodos para el análisis de clústeres: Clúster de Medias K, Clúster Jerárquico y Clúster de Dos pasos.
K-means cluster es un método para agrupar rápidamente grandes conjuntos de datos. El investigador define el número de clusters por adelantado. Esto es útil para probar diferentes modelos con un número supuesto diferente de clústeres.
El cluster jerárquico es el método más común. Genera una serie de modelos con soluciones de clúster de 1 (todos los casos en un clúster) a n (cada caso es un clúster individual). El clúster jerárquico también funciona con variables en lugar de casos; puede agrupar variables de una manera algo similar al análisis factorial. Además, el análisis jerárquico de clústeres puede manejar datos nominales, ordinales y de escala; sin embargo, no se recomienda mezclar diferentes niveles de medición.
El análisis de clústeres en dos pasos identifica las agrupaciones ejecutando primero la agrupación previa y luego ejecutando métodos jerárquicos. Debido a que utiliza un algoritmo de clúster rápido por adelantado, puede manejar grandes conjuntos de datos que tardarían mucho tiempo en calcularse con métodos de clúster jerárquicos. A este respecto, es una combinación de los dos enfoques anteriores. La agrupación en clústeres de dos pasos puede manejar datos de escala y ordinales en el mismo modelo, y selecciona automáticamente el número de clústeres.
El análisis jerárquico de clústeres sigue tres pasos básicos: 1) calcular las distancias, 2) vincular los clústeres y 3) elegir una solución seleccionando el número correcto de clústeres.
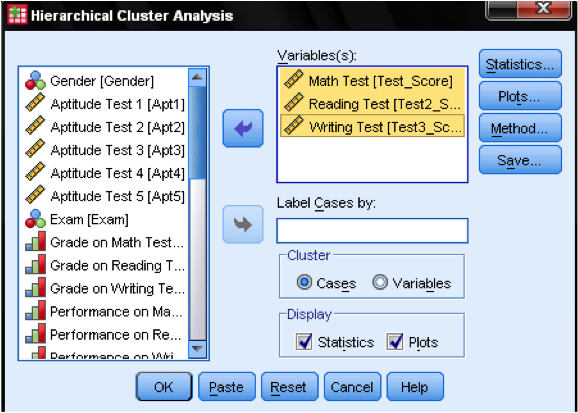
Primero, tenemos que seleccionar las variables en las que basamos nuestros clústeres. En la ventana de diálogo añadimos las pruebas de matemáticas, lectura y escritura a la lista de variables. Como queremos agrupar casos, dejamos el resto de las marcas en el valor predeterminado.
En el cuadro de diálogo Estadísticas can podemos especificar si queremos generar la matriz de proximidad (estas son las distancias calculadas en el primer paso del análisis) y la pertenencia predicha al clúster de los casos en nuestras observaciones. Una vez más, dejamos todas las configuraciones por defecto.

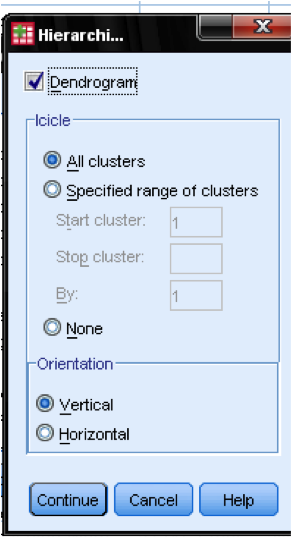
En el cuadro de diálogo de Parcelas… debemos agregar el Dendrograma. El Dendrograma mostrará gráficamente cómo se fusionan los clústeres y nos permite identificar cuál es el número apropiado de clústeres.
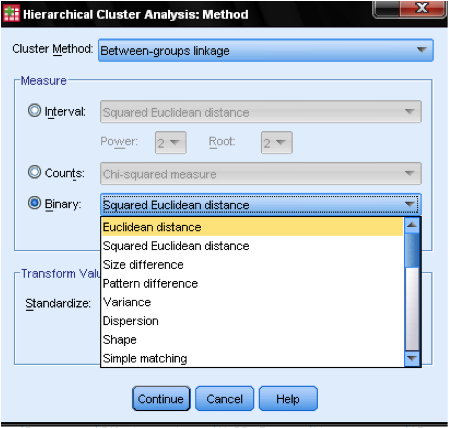
El Método de cuadro de diálogo allows nos permite especificar la medida de distancia y el método de agrupación en clústeres. Primero, necesitamos definir la medida de distancia correcta. SPSS ofrece tres grandes bloques de medidas de distancia para datos de intervalos (escala), conteos (ordinales) y binarios (nominales).
Para datos de intervalos, el más común es la Distancia Euclidiana cuadrada. Se basa en la Distancia euclidiana entre dos observaciones, que es la raíz cuadrada de la suma de distancias cuadradas. Dado que la Distancia euclidiana es cuadrada, aumenta la importancia de las distancias grandes, al tiempo que debilita la importancia de las distancias pequeñas.

Si tenemos datos ordinales (recuentos) podemos seleccionar entre Chi-Cuadrado o un Chi-Cuadrado estandarizado llamado Phi-Cuadrado. Para datos binarios, la Distancia Euclidiana Cuadrada se usa comúnmente.

En nuestro ejemplo, elegimos Intervalo y Distancia Euclidiana Cuadrada.
a continuación, tenemos que elegir el Método de Clúster. Por lo general, las opciones son el enlace entre grupos (distancia entre clústeres es la distancia promedio de todos los puntos de datos dentro de estos clústeres), el vecino más cercano (enlace único: distancia entre clústeres es la distancia más pequeña entre dos puntos de datos), el vecino más lejano (enlace completo: distancia es la distancia más grande entre dos puntos de datos) y el método de Ward (distancia es la distancia de todos los clústeres al gran promedio de la muestra). El enlace único funciona mejor con cadenas largas de racimos, mientras que el enlace completo funciona mejor con manchas densas de racimos. El enlace entre grupos funciona con ambos tipos de clúster. Se recomienda utilizar un solo enlace primero. Aunque el enlace único tiende a crear cadenas de grupos, ayuda a identificar valores atípicos. Después de excluir estos valores atípicos, podemos pasar al método de Ward. El método de Ward utiliza el valor F (como en ANOVA) para maximizar la importancia de las diferencias entre los grupos.
Una última consideración es la normalización. Si las variables tienen diferentes escalas y medias, es posible que deseemos estandarizar las puntuaciones Z o centrar la escala. También podemos transformar los valores a valores absolutos si tenemos un conjunto de datos donde esto podría ser apropiado.