CIRCUNFERENCIA Y CÓMO ENCONTRAR
Hay algunas maneras de encontrar la circunferencia de la tubería y el tubo redondo. Conocer la circunferencia es clave para construir plantillas precisas para usar con tuberías. Cuanto más precisos sean sus números al desarrollar esta plantilla, mejor ajuste tendrá. Como con cualquier cosa, la práctica y la experiencia en la creación de plantillas también aumentarán la precisión.
El método más utilizado para calcular la circunferencia es usar la fórmula de Pi x diámetro. El tubo redondo de 6 «OD tiene una circunferencia de 18.85″. 6″x Pi = 18,85». Cuando se trata de trabajar con tuberías, debe tener en cuenta que las tuberías se miden nominalmente. Esto significa que la tubería de 6″ no es de 6″ OD. Afortunadamente, todos los fabricantes de tubos siguen un estándar y hay un sinnúmero de tablas y gráficos que enumeran todos los tamaños de tubos e incluso incluyen la circunferencia de todos los tamaños. Consulte el índice para localizar estas tablas, gráficos y otra información.
En las siguientes secciones comenzaremos a desarrollar plantillas para usar con pipe. No importa la complejidad de la plantilla, hay varios conceptos clave que se utilizan con todos ellos, incluida la determinación de la circunferencia. Solo presentaremos estos conceptos en detalle una vez, si necesita ayuda, consulte las secciones anteriores.
Estaremos hablando de dividir la circunferencia de la tubería en varias partes iguales que ayudarán a desarrollar la plantilla. Nos referiremos a estas líneas como líneas de elementos. Cuantas más líneas de elementos tenga, más preciso será el ajuste.
Como se dijo anteriormente, hay muchas maneras en que los artesanos han encontrado soluciones a problemas complejos, este libro ofrece una de esas.
A continuación tenemos un tubo de 4″. Al referirnos a la tabla, podemos ver que el diámetro exterior de esa tubería es de 4,50″. También en el gráfico vemos que tiene una circunferencia total de 14.125″. Para este libro, dividiremos todas las circunferencias en 16 espacios iguales en los que se convertirán en líneas de elementos. El práctico gráfico en la parte posterior también nos muestra el espaciado para dividir la circunferencia en 16 partes, así como 12, 8, 6, 4 y 2. Recuerde, cuantas más líneas de elementos tenga, más precisa será su plantilla. Si no tuviéramos el gráfico, tendríamos que dividir la circunferencia total por el número de espacios necesarios. Se requerirá un poco de redondeo al hacer esto, pero debe tener en cuenta que estar apagado 1/16″, 16 veces terminará por estar apagado por un 1″completo.
Si divide 14.125 por 16, termina en .883. El gráfico en el estado de atrás .875. .875, o 7/8″ es mucho más fácil trabajar con una cinta métrica que .883. La diferencia es de aproximadamente 1/132 por línea, esto será aceptable.
Para comenzar, dibujaremos una vista lateral que mostrará la altura de nuestra sección de tubería. Ahora tenemos que estirar el brazo. Sabemos que la circunferencia es 14.125. Podemos dibujar una vista vertical adyacente a una tubería y luego extender las líneas horizontales (que se muestran en rojo) que son las líneas superior e inferior desde la vista lateral para establecer la altura total de la tubería y ejecutarlas a una longitud de 14.125″. Una vez completada la altura y el estiramiento, estamos listos para colocar las líneas de elementos.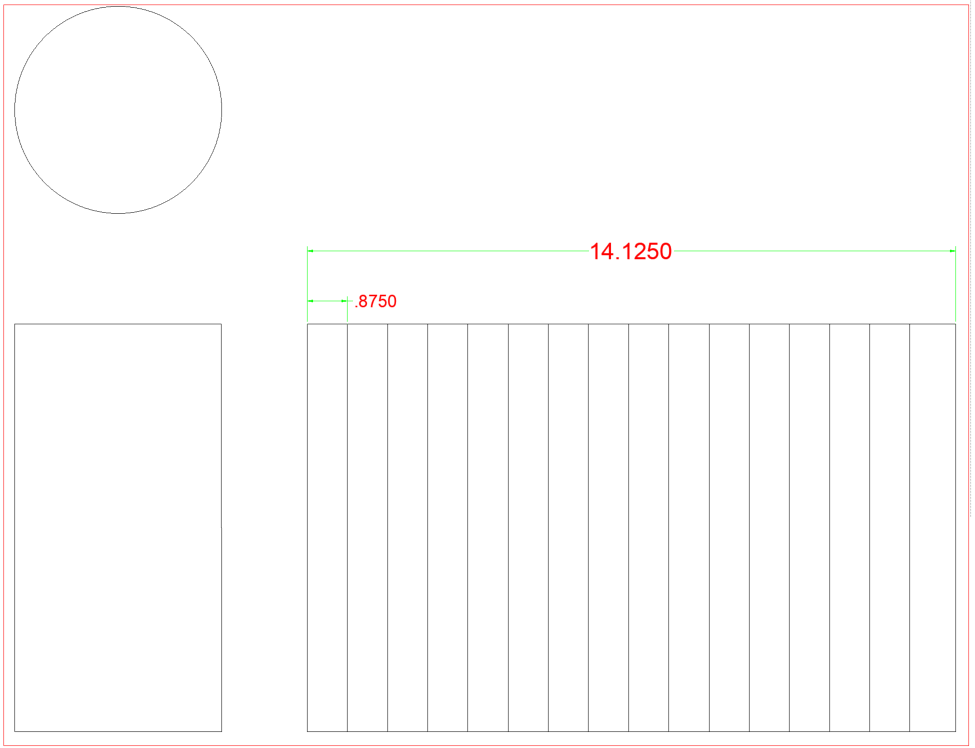
Cuando trabaje con plantillas de tuberías y desarrollo, necesitará repasar algunas geometrías básicas y la bisección de ángulos. Usaremos una brújula para esta tarea.
A continuación tenemos una CABINA en ángulo con un vértice del punto A.
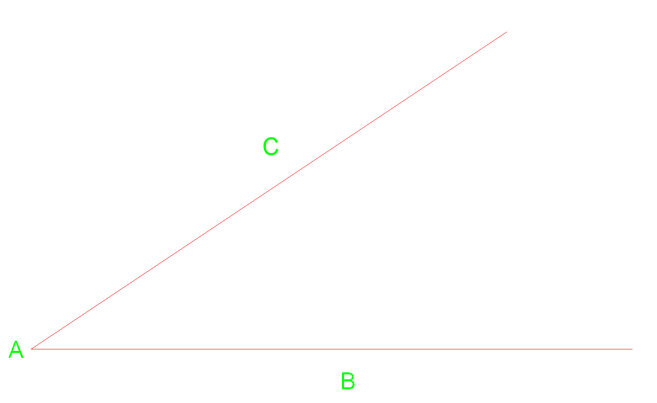
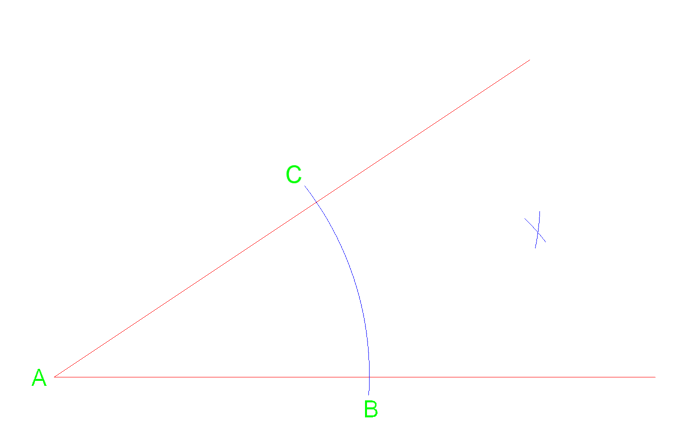
Primero podemos dibujar un arco desde el vértice A que cruza la línea cerca del punto C & B. Desde esas dos intersecciones podemos dibujar dos arcos adicionales a la derecha.
Desde el vértice A dibuja una línea que cruza en el punto D donde el arco se interseca.
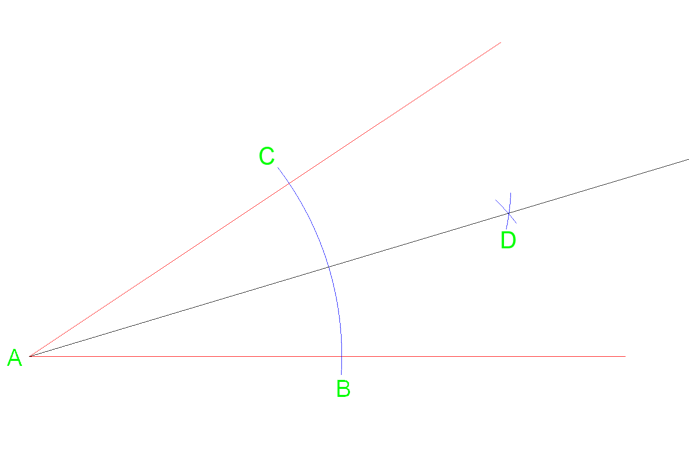
El uso de este método dividirá por igual el ángulo en dos ángulos de la misma medición. Este método y puede repetirse si es necesario para dividirlo de nuevo en 4 partes iguales.
Probemos un método similar en un círculo. El círculo dibujado tiene un diámetro de 3″, por lo que un radio de 1½».
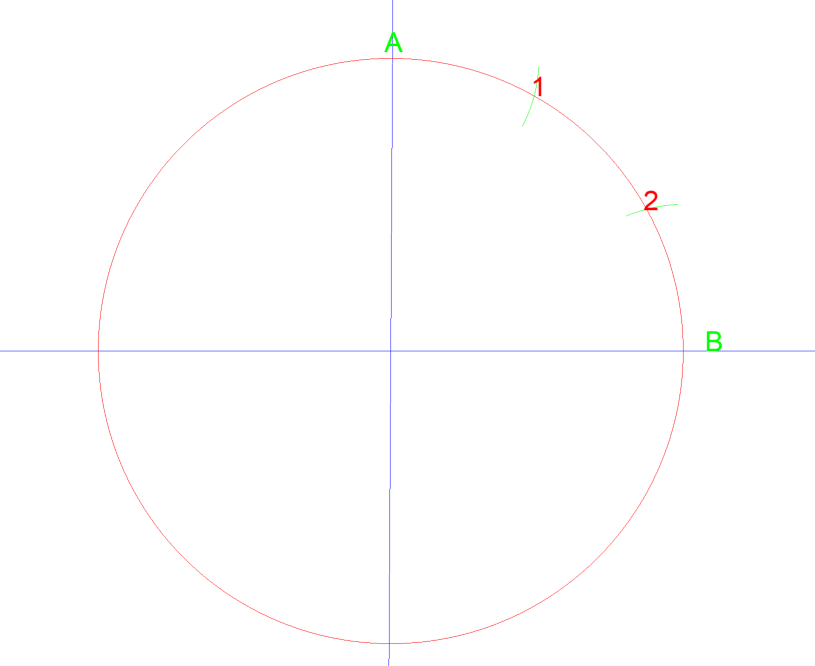
Al establecer su brújula en el radio del círculo, 1 ½ » y luego dibujar un arco desde el punto A y luego B, se cruzan en 1 & 2. Si luego dibuja una línea desde el centro del círculo hasta cada punto, simplemente divide ese cuarto del círculo en tres partes iguales. Ver a continuación…
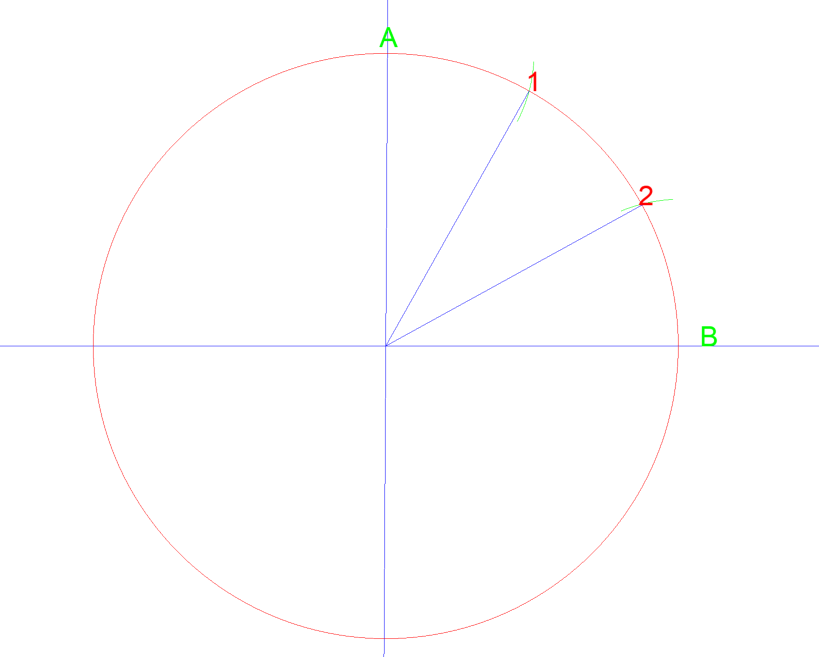
Si luego haces esto de nuevo entre A, 1, 2, & B, puedes dividir ese cuarto de círculo en 6 áreas iguales.
Como mencionamos brevemente anteriormente, usamos números para ayudar a alinear dónde se conectarán las líneas. Estas líneas se utilizarán cuando unamos dos o más partes para hacer un solo ensamblaje. A medida que continuemos, comprenderá mejor cómo funciona este sistema de numeración.