FDTD en FDM-algoritmen voor de MHOF-analyse
optisch licht is elektromagnetische golf in de natuur, en dus zijn voortplantingseigenschappen worden beheerst door de wetten van de elektrodynamica die collectief bekend staan als Maxwell ‘ s vergelijkingen. Het is bekend dat de geleiding van lichtsignalen in de MHOF met fotonische bandgap structuren berust op constructieve interferentie effect als gevolg van de periodieke opstelling van identieke luchtgaten. Aan de andere kant, wanneer de luchtgaten willekeurig worden in grootte, locatie of beide, vindt het fenomeen van totale interne reflectie plaats en het indexverschil tussen de kern en de bekleding zorgt voor lichtopsluiting en dus lichtgeleiding langs de vezel. Hoewel de voortplantingskenmerken van ingewikkelde structuren zoals willekeurige MHOFs niet gemakkelijk kunnen worden berekend met behulp van analytische methoden, zijn er manieren om elektromagnetische problemen numeriek op te lossen.
in deze paragraaf worden twee numerieke technieken van eindige verschiltijddomein (FDTD) en eindige verschilmethode (FDM) behandeld met het oog op uitbreiding van de analyse van holey optische vezels met willekeurige luchtgatdistributies. Elk van deze technieken heeft bepaalde voordelen. Met behulp van de FDTD-methode wordt het continue elektromagnetische veld in een eindig volume van de ruimte bemonsterd op verschillende punten in een ruimterooster en op gelijke bemonsteringspunten in de tijd. De bemonsterde gegevens op de punten worden gebruikt voor numerieke berekeningen van toegestane modi, zonder dat er onechte modusoplossingen worden gegenereerd, in een bepaalde golfgeleider. Hoewel de FDTD-methode een effectieve techniek is voor de berekening van propagatieconstanten van geleide modi, is deze niet geschikt voor de evaluatie van veldverdelingen in individuele modi. Dit komt omdat de bron een impulsfunctie is in het tijddomein die een oneindig spectrum beslaat, dus velddistributieoplossingen zijn superpositie van alle mogelijke modi. Om dit probleem met propagatieconstanten beschikbaar van FDTD te verlichten, worden individuele modus velddistributies verkregen met behulp van de FDM, die snel en gemakkelijk individuele modus veldoplossingen kan bieden.
de FDTD heeft de afgelopen jaren een aanzienlijke populariteit gewonnen, omdat deze methode robuuste oplossingen biedt, gebaseerd op Maxwell ‘ s vergelijkingen , en gemakkelijk complexe materiaaleigenschappen kan verwerken. Een willekeurig materieel object kan worden benaderd door eenheidscellen op te bouwen waarvoor de posities van de veldcomponenten worden afgevoerd met de gewenste waarden van permittiviteit en permeabiliteit. Zodra de geometrie van het object is gespecificeerd in het numerieke simulatiegebied, wordt de bronconditie ergens in het gebied gemodelleerd. Aanvankelijk wordt aangenomen dat alle velden binnen het rekendomein identiek nul zijn. Vervolgens wordt een incidentgolf afgedwongen om de numerieke berekeningsregio in te voeren.
gebruik makend van het MKS-systeem van eenheden, laten we eerst Maxwell ‘ s curl-vergelijkingen, uitgedrukt als:
waarbij ε de elektrische permittiviteitsconstante is in F/m En μ de magnetische permeabiliteitsconstante in H / m.door de kruluitdrukkingen uit te breiden en soortgelijke componenten gelijk te stellen, wordt het systeem van zes gekoppelde partiële differentiaalvergelijkingen gevormd voor de FDTD-analyse van elektromagnetische golfinteracties met algemene driedimensionale objecten. Opgemerkt moet worden dat de elektrische en magnetische veldcomponenten (Ex, Ey, Ez, Hx, Hy en Hz) met elkaar verbonden zijn. Dat wil zeggen dat Maxwell ‘ s vergelijkingen niet direct elektrische en magnetische veldwaarden opleveren, maar eerder de mate van verandering tussen elektrische en magnetische veldwaarden relateren.
uitgaande van een centrale eindige verschilbenadering voor ruimte-en tijdderivaten met nauwkeurigheid tot de tweede orde, kunnen de volgende benaderingen als representatieve voorbeelden in een driedimensionale (3D) FDTD-formulering worden ontwikkeld:
waarbij i, j, k, en n gehele getallen zijn voor Δx, Δy, Δz, en ∆ T, respectievelijk, als de ruimte en tijd te verplaatsen .
aangezien optische vezels zoals MHOFs over het algemeen geen variaties in de voortplantingsrichting hebben en variaties van materiaaleigenschappen beperkt zijn tot de dwarsrichtingen zoals weergegeven in Figuur 3, kan de 3D FDTD-formulering worden vereenvoudigd tot het compacte tweedimensionale (2D) FDTD-algoritme . Door phasor-notatie met de axiale propagatieconstante (β) te gebruiken, worden de partiële derivaten van de eerste orde met betrekking tot z vervangen door-jß, omdat de Z-afhankelijkheid van velden exp(-jßz) is. En twee aangrenzende velden die nodig zijn voor de eerste-orde afgeleiden in het gediscretiseerde ruimtegebied kunnen worden weergegeven door een veld op het middenpunt tussen hen. Op basis van deze twee feiten wordt de volgende formule als voorbeeld verkregen:
het resulterende 2D-algoritme maakt gebruik van een aanzienlijke vermindering van de vereiste toewijzing van computergeheugen en looptijd. Dus voor computerberekening van willekeurige golfgeleiders die uniform zijn langs de richting van golfvoortplanting, is alleen modellering van de doorsneden van golfgeleiders voldoende.
samen met dit efficiënte algoritme moeten oneindige media in de 2D-ruimte voor een willekeurig elektromagnetisch object zorgvuldig gemodelleerd worden, omdat het computergeheugen in het rekengebied beperkt is, zelfs met geavanceerde huidige technologie. Om regio ‘ s tot in het oneindige te modelleren, wordt een perfect matched layer (PML) als een zeer effectieve absorberende grensconditie (ABC) ontworpen op de buitenste roostergrens van een rekendomein. Idealiter is het absorberende medium slechts zo dik als een paar roostercellen, zeer absorberend, reflectieloos voor alle indringende golven en effectief over het volledige bereik van werkende golflengten.
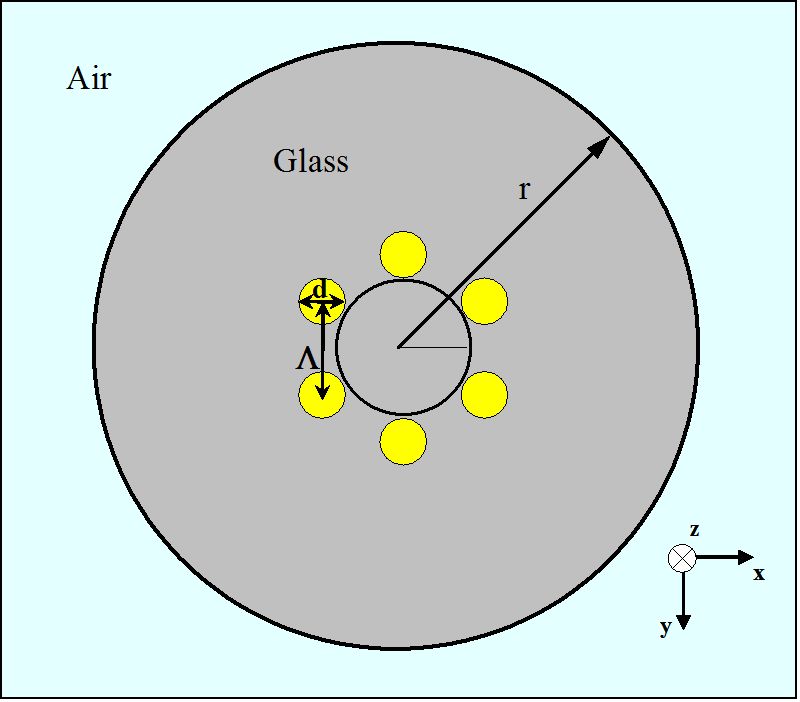
Figuur 3.
schema van een dwarsdoorsnede voor een MHOF met één laag luchtgaten in een zeshoekige opstelling
net als de ontwikkeling van het FDTD algoritme, kan de FDM formulering worden afgeleid van de gekoppelde Maxwell vergelijkingen . Voor continue golven in lineaire en isotrope media resulteert het combineren van MKN (2) en (3) in de volgende vectoriële golfvergelijking:
waarbij n de brekingsindex is en k0 de propagatieconstante in de vrije ruimte. Veel golfgeleiders, zoals optische vezels, kunnen worden gezien als z-invariante of stuksgewijze z-invariante structuren. Voor deze structuren varieert de brekingsindex n(x,y,z) langzaam langs de voortplantingsrichting z, wat geldt voor de meeste fotonische geleide-Golf apparaten. Door de vectoridentiteit van∇×∇×=∇(∇⋅)−∇2, Eq (8)kan worden geschreven als
ook met de redelijke aanname van verwaarloosbare tijdsafhankelijkheid langs de Z-as, kan de FDM-formulering zoals in EQ (9) worden geïmplementeerd door ruimtelijke afgeleiden te vervangen door eindige verschilbenaderingen. Hier wordt opgemerkt dat de transversale component van (9)
waar het subscript “t” staat voor de transversale componenten. Aangezien de longitudinale component gemakkelijk kan worden verkregen door toepassing van de volgende nuldivergentie (Gauss ‘ wet) beperking:
de transversale componenten zijn voldoende om de volledige vectoriële aard van het elektromagnetische veld in een optische golfgeleider te beschrijven.
voor het eerste onderzoek naar de geleidingseigenschappen van MHOFs wordt de in Figuur 3 getoonde optische vezel door de computer geanalyseerd. In het algemeen kan de mhof-geometrie worden beschreven met twee parameters, spoedlengte (Λ) en diameter (d), zoals aangegeven in Figuur 3. Hier is de spoedlengte de afstand tussen de centra van twee dichtstbijzijnde luchtgaten met de cilindrische vorm. Voor de MHOF van Figuur 3 heeft elk klein luchtgat een diameter van 1,4 µm, wat een zeshoek vormt met Λ = 1,7 µm. Het glazen gedeelte rondom de zes luchtgaten van de gele gebieden heeft een brekingsindex van 1,45. De buitenste straal (r) van de holeyvezel wordt verondersteld 10 µm te zijn. Ook de buitenregio van de MHOF is lucht.
zodra de doorsnede van een holeyvezel in een juist rekendomein is gedefinieerd, kan de FDTD-simulatie worden uitgevoerd met verschillende gespecificeerde parameters, zoals τ bij het definiëren van een Gaussiaanse bron, Δt voor stabiele simulatie, het totale aantal (ntot) tijdstappen voor het nemen van gegevens in het tijddomein, en redelijke waarden van β. Om numerieke divergentie te voorkomen en de stabiliteit van het FDTD-algoritme te garanderen, moet hier een geschikte Δt worden gekozen om aan de volgende stabiliteitsvoorwaarde te voldoen. :
waarbij cM de maximale golffasesnelheid binnen een bepaald numeriek model is. Samenvattend het mechanisme achter de FDTD-analyse, de computersimulatie gaat door de volgende stappen:
-
Kies de juiste parameter waarden (τ, ∆ T, ntot, en β)
-
Gegevens samplen van een veld component in het tijdsdomein
-
Neem de Fourier-transformatie van de tijd gegevens
-
Voor spectrale gegevens van een veld component
-
Kies de modus frequenties geassocieerd met de β-waarde
-
het Verzamelen van β-en mode-frequentie-gegevens
-
Maak een plot van de mode index versus golflengte
Figuur 4 illustreert de kenmerkende rondingen, die zijn verkregen van de FDTD berekening, voor de eerste drie lagere-orde modi van de MHOF gedefinieerd in Figuur 3.
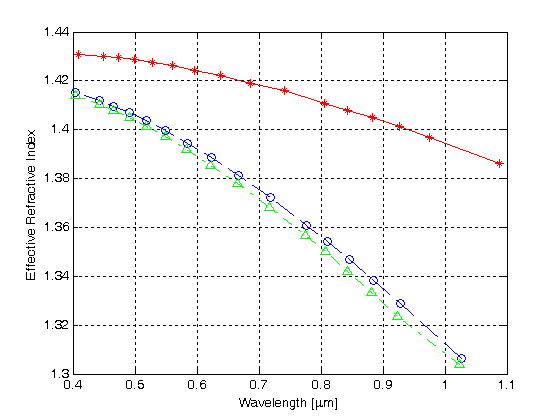
Figuur 4.
effectieve brekingsindex versus golflengte voor de eerste drie modi in een MHOF met één laag luchtgaten
de rode kromme met de stersymbolen toont de genormaliseerde propagatieconstante voor de eerste modus versus golflengte, terwijl de blauwe en groene krommen de genormaliseerde propagatieconstanten voor respectievelijk de tweede en de derde modus tonen. De resultaten geven aan dat de HMOF met een enkele zeshoekige luchtgatbekledingslaag multimode geleiding ondersteunt.