Was ist die Clusteranalyse?
Die Clusteranalyse ist eine explorative Analyse, die versucht, Strukturen innerhalb der Daten zu identifizieren. Die Clusteranalyse wird auch als Segmentierungsanalyse oder Taxonomieanalyse bezeichnet. Genauer, Es wird versucht, homogene Gruppen von Fällen zu identifizieren, wenn die Gruppierung bisher nicht bekannt ist. Da es explorativ ist, unterscheidet es nicht zwischen abhängigen und unabhängigen Variablen. Die verschiedenen Clusteranalysemethoden, die SPSS anbietet, können Binär-, Nominal-, Ordinal- und Skalierungsdaten (Intervall oder Verhältnis) verarbeiten.
Die Clusteranalyse wird häufig in Verbindung mit anderen Analysen (z. B. der Diskriminanzanalyse) verwendet. Der Forscher muss in der Lage sein, die Clusteranalyse basierend auf seinem Verständnis der Daten zu interpretieren, um festzustellen, ob die durch die Analyse erzeugten Ergebnisse tatsächlich aussagekräftig sind.
Typische Forschungsfragen Die Clusteranalyse beantwortet wie folgt:
- Medizin – Was sind die diagnostischen Cluster? Um diese Frage zu beantworten, würde der Forscher einen diagnostischen Fragebogen erstellen, der mögliche Symptome (z. B. in Psychologie, Angstzuständen, Depressionen usw.) enthält.). Die Clusteranalyse kann dann Gruppen von Patienten identifizieren, die ähnliche Symptome haben.
- Marketing – Was sind die Kundensegmente? Um diese Frage zu beantworten, kann ein Marktforscher eine Umfrage zu Bedürfnissen, Einstellungen, Demografie und Verhalten von Kunden durchführen. Der Forscher kann dann Clusteranalyse verwenden, um homogene Gruppen von Kunden zu identifizieren, die ähnliche Bedürfnisse und Einstellungen haben.
- Bildung – Was sind Studentengruppen, die besondere Aufmerksamkeit benötigen? Forscher können psychologische, Eignungs- und Leistungsmerkmale messen. Eine Clusteranalyse kann dann identifizieren, welche homogenen Gruppen unter den Schülern existieren (z. B. Leistungsträger in allen Fächern oder Schüler, die in bestimmten Fächern hervorragende Leistungen erbringen, in anderen jedoch versagen).
- Biologie – Was ist die Taxonomie der Arten? Forscher können einen Datensatz verschiedener Pflanzen sammeln und verschiedene Attribute ihrer Phänotypen notieren. Eine Clusteranalyse kann diese Beobachtungen in eine Reihe von Clustern gruppieren und dabei helfen, eine Taxonomie von Gruppen und Untergruppen ähnlicher Pflanzen aufzubauen.
Andere Techniken, die Sie möglicherweise ausprobieren möchten, um ähnliche Beobachtungsgruppen zu identifizieren, sind Q-Analyse, mehrdimensionale Skalierung (MDS) und latente Klassenanalyse.
Die Clusteranalyse in SPSS
Unsere Forschungsfrage für dieses Beispiel der Clusteranalyse lautet wie folgt:
Welche homogenen Cluster von Studenten entstehen auf der Grundlage standardisierter Testergebnisse in Mathematik, Lesen und Schreiben?
In SPSS finden Sie Clusteranalysen unter Analysieren/Klassifizieren…. SPSS bietet drei Methoden für die Clusteranalyse: K-Means Cluster, Hierarchical Cluster und Two-Step Cluster.
K-means cluster ist eine Methode zum schnellen Clustern großer Datensätze. Die Forscher definieren die Anzahl der Cluster im Voraus. Dies ist nützlich, um verschiedene Modelle mit einer unterschiedlichen angenommenen Anzahl von Clustern zu testen.
Hierarchischer Cluster ist die gebräuchlichste Methode. Es generiert eine Reihe von Modellen mit Clusterlösungen von 1 (alle Fälle in einem Cluster) bis n (jeder Fall ist ein einzelner Cluster). Hierarchischer Cluster arbeitet auch mit Variablen im Gegensatz zu Fällen; Es kann Variablen ähnlich wie bei der Faktorenanalyse gruppieren. Darüber hinaus kann die hierarchische Clusteranalyse Nominal-, Ordinal- und Skalendaten verarbeiten; es wird jedoch nicht empfohlen, verschiedene Messebenen zu mischen.
Die zweistufige Clusteranalyse identifiziert Gruppierungen, indem zuerst Pre-Clustering und dann hierarchische Methoden ausgeführt werden. Da es im Voraus einen schnellen Cluster-Algorithmus verwendet, kann es große Datensätze verarbeiten, deren Berechnung mit hierarchischen Cluster-Methoden lange dauern würde. In dieser Hinsicht ist es eine Kombination der beiden vorherigen Ansätze. Das zweistufige Clustering kann Skalierungsdaten und Ordinaldaten im selben Modell verarbeiten und wählt automatisch die Anzahl der Cluster aus.
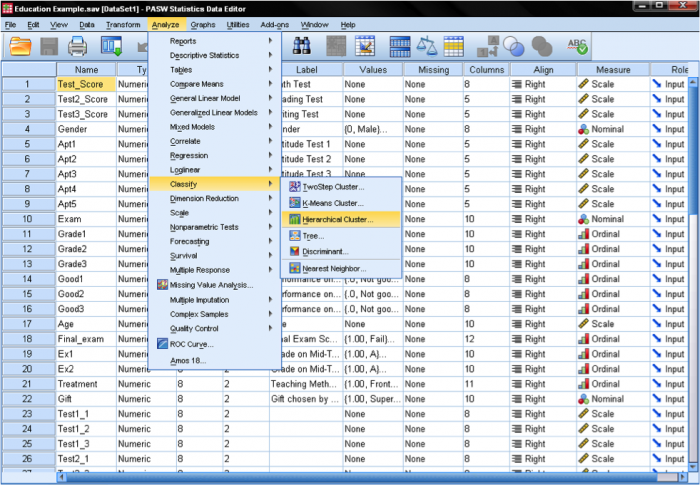
Die hierarchische Clusteranalyse folgt drei grundlegenden Schritten: 1) Berechnen Sie die Entfernungen, 2) Verknüpfen Sie die Cluster und 3) Wählen Sie eine Lösung, indem Sie die richtige Anzahl von Clustern auswählen.
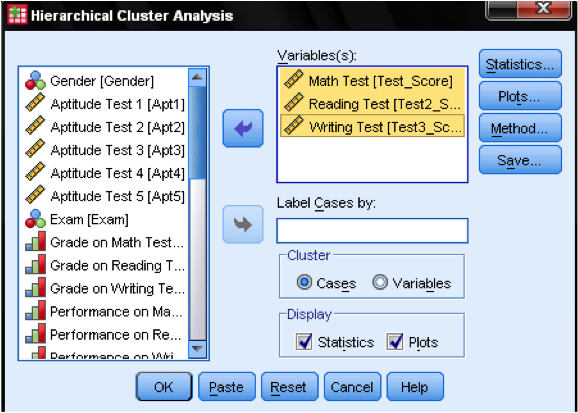
Zuerst müssen wir die Variablen auswählen, auf denen unsere Cluster basieren. Im Dialogfenster fügen wir die Mathe-, Lese- und Schreibtests zur Variablenliste hinzu. Da wir Fälle gruppieren möchten, lassen wir den Rest der Häkchen auf dem Standardwert.
Im Dialogfeld Statistik… können wir festlegen, ob wir die Näherungsmatrix (das sind die im ersten Schritt der Analyse berechneten Entfernungen) und die vorhergesagte Clusterzugehörigkeit der Fälle in unseren Beobachtungen ausgeben möchten. Auch hier lassen wir alle Einstellungen auf Standard.

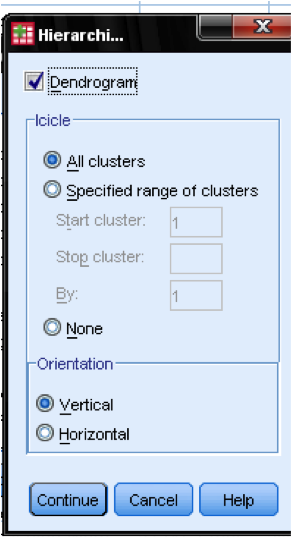
Im Dialogfeld Plots … sollten wir das Dendrogramm hinzufügen. Das Dendrogramm zeigt grafisch, wie die Cluster zusammengeführt werden, und ermöglicht es uns, die entsprechende Anzahl von Clustern zu identifizieren.
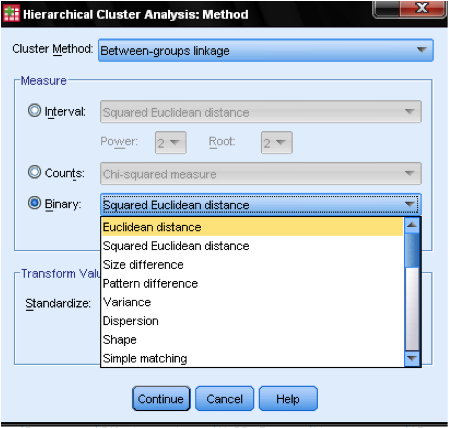
Im Dialogfeld Methode… können wir das Entfernungsmaß und die Clustermethode angeben. Zuerst müssen wir das richtige Entfernungsmaß definieren. SPSS bietet drei große Blöcke von Entfernungsmaßen für Intervall- (Skala-), Zählungswerte (Ordinal-) und Binärdaten (Nominaldaten).
Für Intervalldaten ist der quadratische euklidische Abstand am häufigsten. Es basiert auf der euklidischen Entfernung zwischen zwei Beobachtungen, die die Quadratwurzel der Summe der quadratischen Entfernungen ist. Da der euklidische Abstand quadriert ist, erhöht er die Bedeutung großer Entfernungen, während er die Bedeutung kleiner Entfernungen schwächt.

Wenn wir Ordinaldaten (Zählungen) haben, können wir zwischen Chi-Quadrat oder einem standardisierten Chi-Quadrat namens Phi-Quadrat wählen. Für binäre Daten wird üblicherweise der quadratische euklidische Abstand verwendet.

In unserem Beispiel wählen wir Intervall und quadratische euklidische Entfernung.
Als nächstes müssen wir die Cluster-Methode auswählen. In der Regel stehen die Verknüpfung zwischen Gruppen (Abstand zwischen Clustern ist die durchschnittliche Entfernung aller Datenpunkte innerhalb dieser Cluster), der nächste Nachbar (einfache Verknüpfung: Abstand zwischen Clustern ist der kleinste Abstand zwischen zwei Datenpunkten), der am weitesten entfernte Nachbar (vollständige Verknüpfung: Abstand ist der größte Abstand zwischen zwei Datenpunkten) und die Ward-Methode (Abstand ist der Abstand aller Cluster zum großen Durchschnitt der Stichprobe) zur Auswahl. Eine einzelne Verknüpfung funktioniert am besten mit langen Clusterketten, während eine vollständige Verknüpfung am besten mit dichten Clusterblöcken funktioniert. Die Verknüpfung zwischen Gruppen funktioniert mit beiden Clustertypen. Es wird empfohlen, zuerst ein einzelnes Gestänge zu verwenden. Obwohl eine einzelne Verknüpfung dazu neigt, Ketten von Clustern zu bilden, hilft sie bei der Identifizierung von Ausreißern. Nachdem wir diese Ausreißer ausgeschlossen haben, können wir zu Wards Methode übergehen. Wards Methode verwendet den F-Wert (wie in ANOVA), um die Signifikanz von Unterschieden zwischen Clustern zu maximieren.
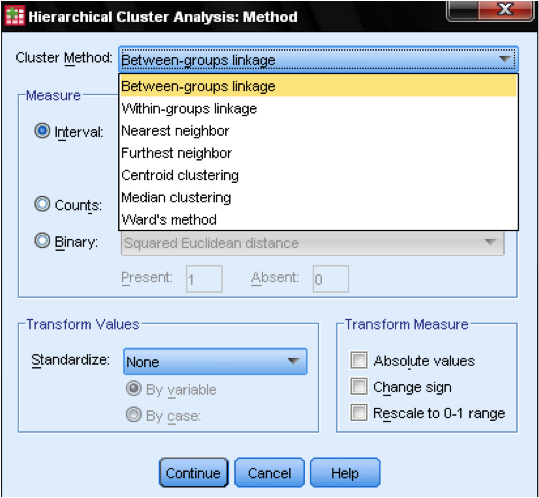
Eine letzte Überlegung ist die Standardisierung. Wenn die Variablen unterschiedliche Skalen und Mittelwerte haben, möchten wir möglicherweise entweder auf Z-Werte standardisieren oder die Skala zentrieren. Wir können die Werte auch in absolute Werte umwandeln, wenn wir einen Datensatz haben, in dem dies angemessen sein könnte.