Laut Noam Chomosky gibt es vier Arten von Grammatiken − Typ 0, Typ 1, Typ 2 und Typ 3. Die folgende Tabelle zeigt, wie sie sich voneinander unterscheiden −
| Grammatiktyp | Grammatik akzeptiert | Sprache akzeptiert | Automat |
|---|---|---|---|
| Typ 0 | Uneingeschränkte Grammatik | Rekursiv aufzählbare Sprache | Turingmaschine |
| Typ 1 | Kontextsensitive Grammatik | Kontextsensitive Sprache | Linear begrenzter Automat |
| Typ 2 | Kontextfreie Grammatik | Kontextfreie Sprache | Pushdown-Automat |
| Typ 3 | Reguläre Grammatik | Reguläre Sprache | Endlicher Zustandsautomat |
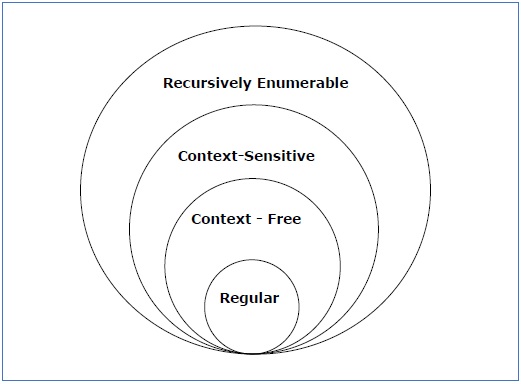
Schauen Sie sich die folgende Abbildung an. Es zeigt den Umfang jeder Art von Grammatik –
Typ-3-Grammatik
Typ-3-Grammatiken generieren reguläre Sprachen. Typ-3-Grammatiken müssen ein einzelnes Nicht-Terminal auf der linken Seite und eine rechte Seite haben, die aus einem einzelnen Terminal oder einem einzelnen Terminal gefolgt von einem einzelnen Nicht-Terminal besteht.
Die Produktionen müssen die Form X → a oder X → aY
haben,wobei X, Y ∈ N (Nicht terminal)
und a ∈ T (Terminal)
Die Regel S → ε ist zulässig, wenn S nicht auf der rechten Seite einer Regel erscheint.
Beispiel
X → ε X → a | aYY → b
Typ – 2-Grammatik
Typ-2-Grammatiken erzeugen kontextfreie Sprachen.
Die Produktionen müssen die Form A → γ
haben, wobei A ∈ N (Nicht terminal)
und γ ∈ (T ∪ N)* (Zeichenfolge von Terminals und Nicht-Terminals).
Diese von diesen Grammatiken erzeugten Sprachen werden von einem nicht deterministischen Pushdown-Automaten erkannt.
Beispiel
S → X a X → a X → aX X → abc X → ε
Typ – 1-Grammatik
Typ-1-Grammatiken erzeugen kontextsensitive Sprachen. Die Produktionen müssen die Form
α A β → α γ β
haben, wobei A ∈ N (Nicht-terminal)
und α, β, γ ∈ (T ∪ N)* (Strings von Terminals und Nicht-Terminals)
Die Strings α und β können leer sein, γ muss jedoch nicht leer sein.
Die Regel S → ε ist zulässig, wenn S nicht auf der rechten Seite einer Regel erscheint. Die von diesen Grammatiken erzeugten Sprachen werden von einem linear begrenzten Automaten erkannt.
Beispiel
AB → AbBc A → bcA B → b
Typ – 0-Grammatik
Typ-0-Grammatiken erzeugen rekursiv aufzählbare Sprachen. Die Produktionen haben keine Einschränkungen. Sie sind jede Phasenstrukturgrammatik einschließlich aller formalen Grammatiken.
Sie erzeugen die Sprachen, die von einer Turing-Maschine erkannt werden.
Das Ergebnis kann die Form α → β haben, wobei α eine Folge von Terminals und Nichtterminals mit mindestens einem Nichtterminal ist und α nicht null sein kann. β ist eine Reihe von Terminals und Nicht-Terminals.
Beispiel
S → ACaB Bc → acB CB → DB aD → Db