FDTD- und FDM-Algorithmen für die MHOF-Analyse
Optisches Licht ist elektromagnetische Welle in der Natur, und so werden seine Ausbreitungseigenschaften durch die Gesetze der Elektrodynamik geregelt, die kollektiv als Maxwell-Gleichungen bekannt sind. Es ist bekannt, dass die Führung von Lichtsignalen im MHOF mit photonischen Bandlückenstrukturen auf dem konstruktiven Interferenzeffekt aufgrund der periodischen Anordnung identischer Luftlöcher beruht. Wenn andererseits die Luftlöcher in Größe, Lage oder beidem zufällig werden, tritt das Phänomen der inneren Totalreflexion auf, und die Indexdifferenz zwischen Kern und Mantel sorgt für eine Lichteinschränkung und damit für eine Lichtführung entlang der Faser. Obwohl die Ausbreitungseigenschaften komplizierter Strukturen wie beliebiger MHOFs mit analytischen Methoden nicht einfach berechnet werden können, gibt es Möglichkeiten, elektromagnetische Probleme numerisch zu lösen.
In diesem Abschnitt werden zwei numerische Techniken der Finite-Differenz-Zeitdomäne (FDTD) und der Finite-Differenz-Methode (FDM) unter Berücksichtigung der Erweiterung auf die Analyse von löchrigen optischen Fasern mit beliebigen Luftlochverteilungen behandelt. Jede dieser Techniken hat bestimmte Vorteile. Mit der FDTD-Methode wird das kontinuierliche elektromagnetische Feld in einem endlichen Raumvolumen an verschiedenen Punkten in einem Raumgitter und zu gleich beabstandeten Abtastzeitpunkten abgetastet. Die abgetasteten Daten an den Punkten werden für numerische Berechnungen zulässiger Moden verwendet, ohne Störmodenlösungen in einem gegebenen Wellenleiter zu erzeugen. Obwohl die FDTD-Methode eine effektive Technik zur Berechnung von Ausbreitungskonstanten von geführten Moden ist, eignet sie sich nicht gut für die Bewertung einzelner Modenfeldverteilungen. Dies liegt daran, dass die Quelle eine Impulsfunktion im Zeitbereich ist, die ein unendliches Spektrum abdeckt, daher sind Feldverteilungslösungen Überlagerung aller möglichen Moden. Um dieses Problem mit Ausbreitungskonstanten zu lindern, die von FDTD verfügbar sind, werden individuelle Modenfeldverteilungen unter Verwendung des FDM erhalten, das schnell und bequem individuelle Modenfeldlösungen bereitstellen kann.
Die FDTD hat in den letzten Jahren an Popularität gewonnen, da diese Methode robuste Lösungen auf der Grundlage von Maxwellschen Gleichungen bietet und komplexwertige Materialeigenschaften problemlos aufnehmen kann. Durch den Aufbau von Einheitszellen, für die Feldkomponentenpositionen mit den gewünschten Werten der Permittivität und Permeabilität angeordnet sind, kann ein beliebiges materielles Objekt angenähert werden. Sobald die Geometrie des Objekts in der numerischen Simulationsregion angegeben ist, wird die Quellbedingung irgendwo in der Region modelliert. Zunächst wird angenommen, dass alle Felder innerhalb der Berechnungsdomäne identisch Null sind. Dann wird eine einfallende Welle erzwungen, um in den numerischen Berechnungsbereich einzutreten.
Unter Verwendung des MKS-Einheitensystems betrachten wir zunächst Maxwells Curl-Gleichungen, ausgedrückt als:
wobei ε die elektrische Permittivitätskonstante in F / m und μ die magnetische Permeabilitätskonstante in H / m ist. Durch Erweitern der Curl-Ausdrücke und Gleichsetzen der ähnlichen Komponenten wird das System von sechs gekoppelten partiellen Differentialgleichungen für die FDTD-Analyse von Wechselwirkungen elektromagnetischer Wellen mit allgemeinen dreidimensionalen Objekten gebildet. Es ist zu beachten, dass die elektrischen und magnetischen Feldkomponenten (Ex, Ey, Ez, Hx, Hy und Hz) miteinander zusammenhängen. Das heißt, die Maxwellschen Gleichungen ergeben nicht direkt elektrische und magnetische Feldwerte, sondern beziehen sich auf die Änderungsrate zwischen elektrischen und magnetischen Feldwerten.
Unter Verwendung einer Finite-Differenzen-Approximation für Raum- und Zeitableitungen mit Genauigkeit zweiter Ordnung können die folgenden Approximationen als repräsentative Beispiele in einer dreidimensionalen (3D) FDTD-Formulierung entwickelt werden:
wobei i, j, k und n ganze Zahlen für Δx, Δy, Δz bzw.
Da optische Fasern wie MHOFs im Allgemeinen keine Variationen entlang der Ausbreitungsrichtung aufweisen und Variationen der Materialeigenschaften auf die Querrichtungen beschränkt sind, wie in Abbildung 3 gezeigt, kann die 3D-FDTD-Formulierung auf den kompakten zweidimensionalen (2D) FDTD-Algorithmus vereinfacht werden. Durch die Verwendung der Phasennotation mit der axialen Ausbreitungskonstante (β) werden die partiellen Ableitungen erster Ordnung in Bezug auf z durch -jß ersetzt, da die z-Abhängigkeit der Felder als exp (-jßz) ist. Und zwei benachbarte Felder, die für die Ableitungen erster Ordnung im diskretisierten Raumbereich erforderlich sind, können durch ein Feld in der Mitte zwischen ihnen dargestellt werden. Basierend auf diesen beiden Tatsachen wird die folgende Formulierung als Beispiel erhalten:
Der resultierende 2D-Algorithmus nutzt eine signifikante Reduzierung der erforderlichen Computerspeicherzuweisung und Laufzeit. Für die rechnerische Berechnung beliebiger Wellenleiter, die entlang der Wellenausbreitungsrichtung einheitlich sind, genügt daher nur die Modellierung der Wellenleiterquerschnitte.
Zusammen mit diesem effizienten Algorithmus müssen unendliche Medien im 2D-Raum für ein beliebiges elektromagnetisches Objekt sorgfältig modelliert werden, da der Computerspeicher selbst mit fortschrittlicher aktueller Technologie im Berechnungsbereich begrenzt ist. Um bis ins Unendliche reichende Bereiche zu modellieren, wird an der äußeren Gittergrenze einer Berechnungsdomäne eine perfekt angepasste Schicht (PML) als hochwirksame absorbierende Randbedingung (ABC) ausgelegt. Im Idealfall ist das absorbierende Medium nur so dick wie einige Gitterzellen, hoch absorbierend, reflexionslos für alle auftreffenden Wellen und über den gesamten Bereich der Betriebswellenlängen wirksam.
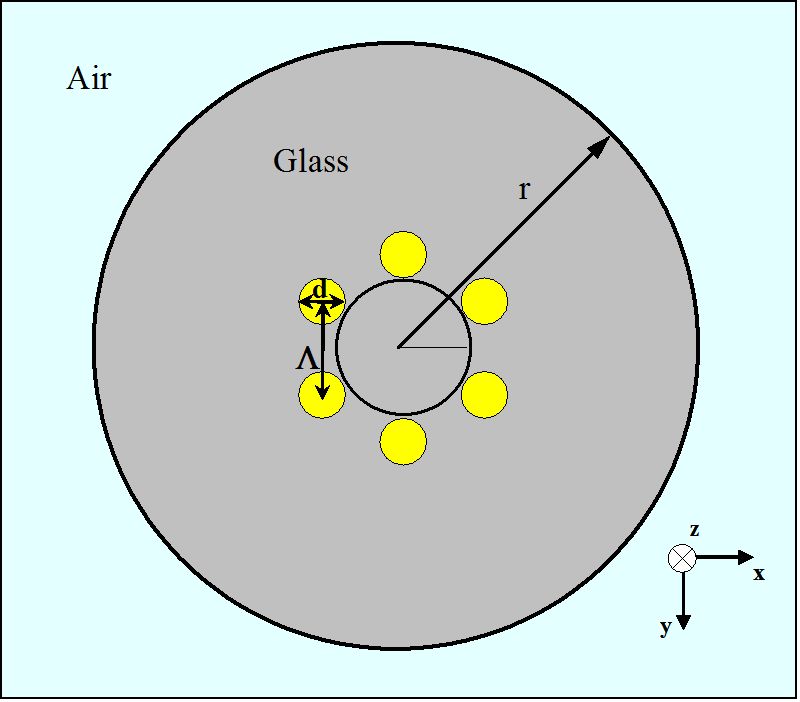
Abbildung 3.
Schematische Darstellung eines Querschnitts für eine M4 mit einer Schicht von Luftlöchern in einer hexagonalen Anordnung
Ähnlich wie bei der Entwicklung des FDTD-Algorithmus kann die FDM-Formulierung aus den gekoppelten Maxwell-Gleichungen abgeleitet werden. Für kontinuierliche Wellen in linearen und isotropen Medien ergibt die Kombination von Eqs (2) und (3) die folgende vektorielle Wellengleichung:
wobei n der Brechungsindex und k0 die Ausbreitungskonstante im freien Raum ist. Viele Wellenleitervorrichtungen, wie optische Fasern, können als z-invariante oder stückweise z-invariante Strukturen betrachtet werden. Für diese Strukturen variiert der Brechungsindex n (x, y, z) langsam entlang der Ausbreitungsrichtung z, was für die meisten photonischen geführten Wellenvorrichtungen gilt. Durch die Verwendung der Vektoridentität von∇×∇×=∇(∇⋅)−∇2, Eq (8) kann geschrieben werden als
Auch mit der vernünftigen Annahme einer vernachlässigbaren Zeitabhängigkeit entlang der z-Achse kann die FDM-Formulierung wie in Eq (9) implementiert werden, indem räumliche Ableitungen durch Finite-Differenzen-Approximationen ersetzt werden. Hier wird angemerkt, dass die Querkomponente von (9)
ist, wobei der Index „t“ für die Querkomponenten steht. Da die Längskomponente leicht durch Anwendung der folgenden Nulldivergenz (Gaußsches Gesetz) erhalten werden kann:
Die Querkomponenten reichen aus, um die vollvektoriellen Naturen des elektromagnetischen Feldes in einem Lichtwellenleiter zu beschreiben.
Für die erste Untersuchung der Führungseigenschaften von MHOFs wird die in Abbildung 3 gezeigte optische Faser computeranalysiert. Im Allgemeinen kann die MHOF-Geometrie mit zwei Parametern beschrieben werden, der Teilungslänge (Λ) und dem Durchmesser (d), wie in Abbildung 3 angegeben. Hier ist die Teilungslänge der Abstand zwischen den Zentren zweier nächstgelegener Luftlöcher mit der zylindrischen Form. Für den M-RING von Abbildung 3 hat jedes kleine Luftloch einen Durchmesser von 1,4 µm und bildet ein Sechseck mit Λ = 1,7 µm. Der die sechs Luftlöcher der gelben Bereiche umgebende Glasanteil hat einen Brechungsindex von 1,45. Der Außenradius (r) der löchrigen Faser wird mit 10 µm angenommen. Auch der Außenbereich des MHOF ist Luft.
Sobald der Querschnitt einer löchrigen Faser in einer geeigneten Berechnungsdomäne definiert ist, kann die FDTD-Simulation mit mehreren spezifizierten Parametern durchgeführt werden, wie z. B. τ bei der Definition einer Gaußschen Quelle, Δt für eine stabile Simulation, die Gesamtzahl (ntot) von Zeitschritten zum Abtasten von Daten in der Zeitdomäne und vernünftige Werte von β. Um numerische Divergenzen zu vermeiden und die Stabilität des FDTD-Algorithmus sicherzustellen, muss hier ein geeignetes Δt ausgewählt werden, um die folgende Stabilitätsbedingung zu erfüllen:
wobei cM die maximale Wellenphasengeschwindigkeit innerhalb eines gegebenen numerischen Modells ist. Die Computersimulation fasst den Mechanismus hinter der FDTD-Analyse zusammen und führt die folgenden Schritte aus:
-
Wählen Sie geeignete Parameterwerte (τ, Δt, ntot und β)
-
Datenabtastung einer Feldkomponente im Zeitbereich
-
Nehmen Sie die Fourier-Transformation der Zeitdaten
-
Spektraldaten einer Feldkomponente abrufen
-
Pick-Mode-Frequenzen, die dem β-Wert zugeordnet sind
-
Sammeln β und modus frequenz daten
-
Erstellen Sie ein Diagramm des Modusindex im Vergleich zur Wellenlänge
Abbildung 4 zeigt die Kennlinien, die aus der FDTD erhalten werden berechnung für die ersten drei Modi niedrigerer Ordnung des in Abbildung 3 definierten MHOF.
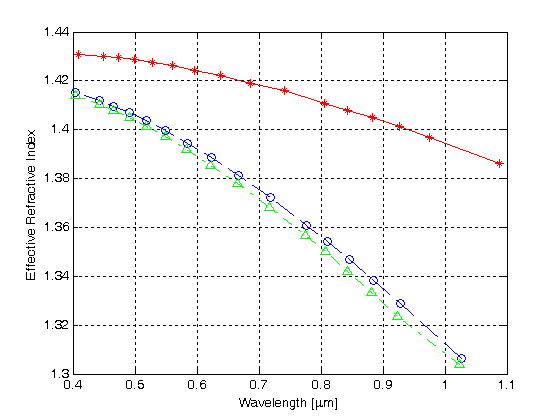
Abbildung 4.
Effektiver Brechungsindex versus Wellenlänge für die ersten drei Moden in einem M2 mit einer Schicht von Luftlöchern
Die rote Kurve mit den Sternsymbolen zeigt die normalisierte Ausbreitungskonstante für die erste Mode gegenüber der Wellenlänge, während die blaue und grüne Kurve die normalisierten Ausbreitungskonstanten für die zweite bzw. die dritte Mode zeigen. Die Ergebnisse zeigen, dass die HMOF mit einer einzigen hexagonalen Luftloch-Mantelschicht Multimode-Führung unterstützt.