omkrets och hur man hittar
det finns några sätt att hitta omkretsen av rör och runda rör. Att känna omkretsen är nyckeln till att bygga exakta mallar för användning med rör. Ju mer exakta dina siffror är när du utvecklar denna mall, desto bättre passform kommer du att ha. Som med allt, övning och erfarenhet av att bygga mallar kommer också att öka noggrannheten.
den mest använda metoden för att räkna omkrets använder formeln för Pi x diameter. 6 ”OD runda röret har en omkrets på 18,85”. 6 ”x Pi=18,85″. När det gäller att arbeta med rör, måste du vara medveten om att röret är mäta nominellt. Detta innebär att 6″ röret är inte 6 ” OD. Lyckligtvis följer alla rörtillverkare en standard och det finns ett oräkneligt antal tabeller och diagram som listar alla rörstorlekar och till och med inkluderar omkretsen av alla storlekar! Se index för att hitta dessa tabeller, diagram och annan information.
under de kommande avsnitten kommer vi att börja utveckla mallar för användning med pipe. Oavsett mallens komplexitet finns det flera nyckelbegrepp som används med dem alla, inklusive bestämning av omkretsen. Vi kommer bara att introducera dessa begrepp i detalj en gång, om du behöver hjälp, se tillbaka till tidigare avsnitt.
vi kommer att prata om att dela rörets omkrets i flera lika delar som hjälper till att utveckla mallen. Vi kommer att hänvisa till dessa linjer som elementlinjer. Ju fler elementlinjer du har desto mer exakt passform.
som nämnts tidigare, det finns många sätt att hantverkare har listat ut lösningar på komplexa problem, Detta är boken erbjuder en av dem.
nedan har vi några 4 ” rör. Genom att hänvisa till diagrammet kan vi se att OD för det röret är 4,50″. På diagrammet ser vi också att det har en total omkrets på 14.125″. För den här boken kommer vi att dela upp alla omkretsar i 16 lika stora utrymmen där elementlinjerna blir. Det praktiska diagrammet på baksidan visar oss också avståndet för att dela omkretsen i 16 delar, samt 12, 8, 6, 4 och 2. Kom ihåg att ju fler elementlinjer du har desto mer exakt blir din mall. Om vi inte hade diagrammet måste du dela den totala omkretsen med antalet utrymmen som behövs. Vissa avrundning kommer att krävas när du gör detta, men du måste vara medveten om att vara av 1/16″, 16 gånger kommer att hamna av med en full 1″.
om du delar 14.125 med 16 hamnar du på .883. Diagrammet i det bakre tillståndet .875. .875, eller 7/8 ” är mycket lättare att arbeta med på ett måttband än .883. Skillnaden är ca 1/132 per rad, detta kommer att vara acceptabelt.
för att komma igång kommer vi att rita en sidovy som visar höjden på vår rörsektion. Nästa måste vi dra i vår stretch-out. Vi vet att omkretsen är 14.125. Vi kan rita en vertikal intill sidovy ett rör och sedan förlänga de horisontella linjerna (visas i rött) som är de övre och nedre linjerna från sidovy för att fastställa rörets totala höjd och köra dem ut till en längd av 14.125″. När vi har höjden och sträckningen klar är vi redo att placera elementlinjerna.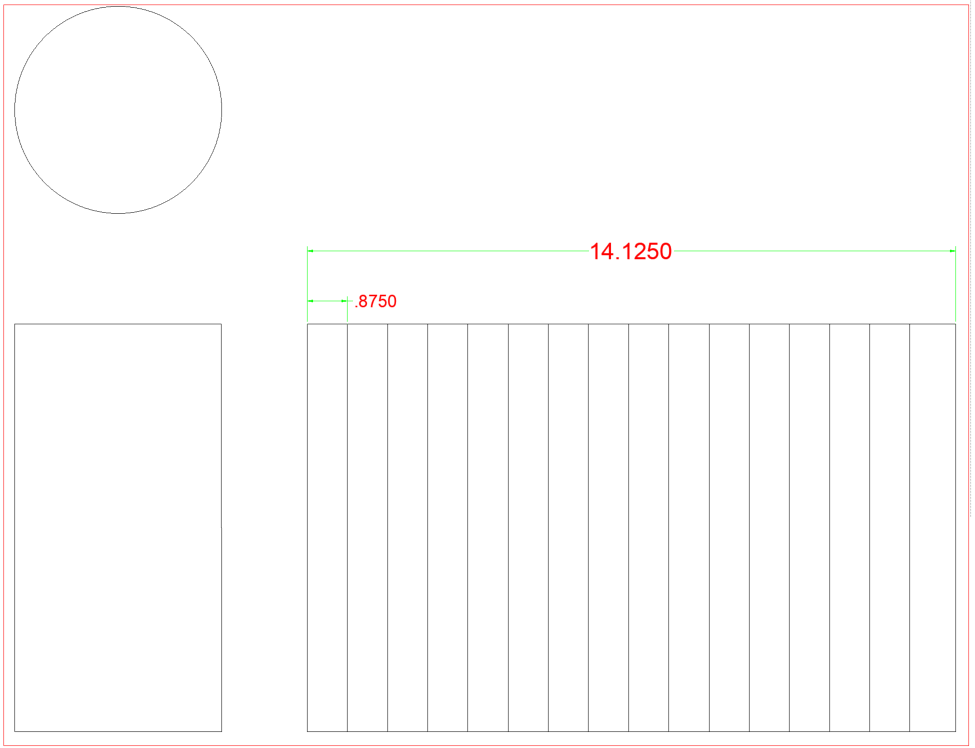
när du arbetar med rör och utveckla mallar måste du fräscha upp några grundläggande geometri och bisecting av vinklar. Vi kommer att använda en kompass för denna uppgift.
nedan har vi vinkelhytt med ett toppunkt av punkt A.
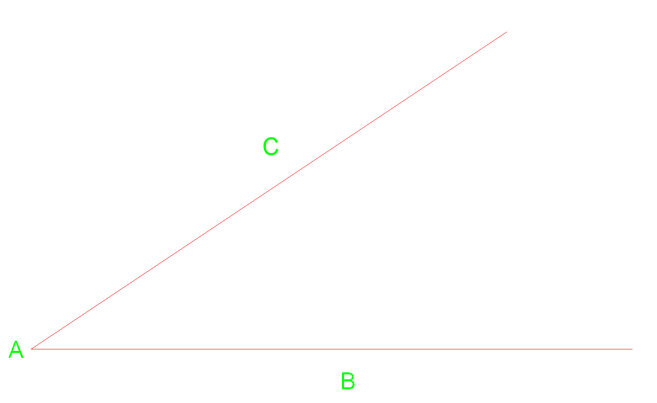
först kan vi rita en båge från vertex A som korsar linjen nära punkt C & B. Från dessa två skärningar kan vi sedan rita ytterligare två bågar till höger.
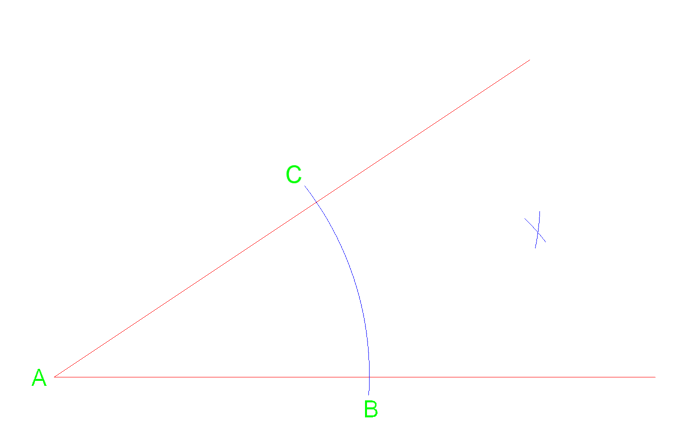
från vertex a rita en linje som korsar vid punkt D där bågen skär.
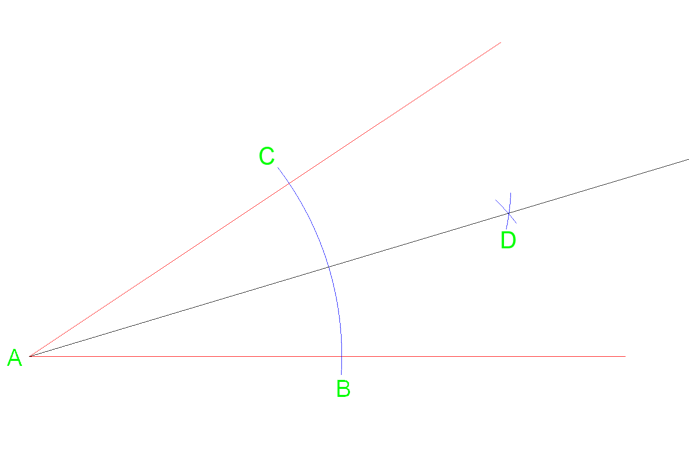
med hjälp av denna metod kommer lika dela vinkeln i två vinklar av samma mätning. Denna metod och kan upprepas om det behövs för att dela upp den igen i 4 lika delar.
låter prova en liknande metod på en cirkel. Den ritade cirkeln har en diameter på 3 ”så en radie på 1 kcal”.
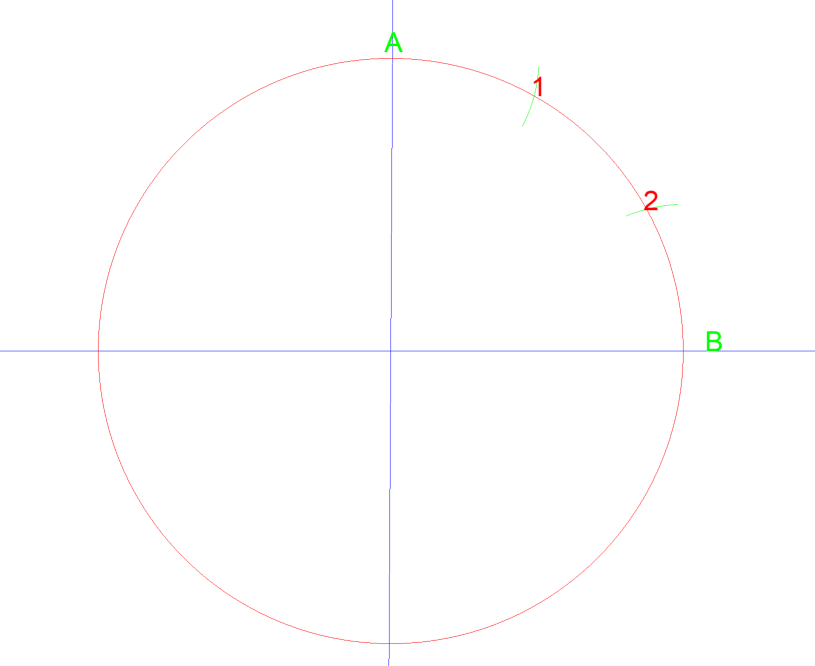
genom att ställa in kompassen till cirkelns radie, 1 msk” och sedan rita en båge från punkt A och sedan B skär de vid 1 & 2. Om du sedan att dra en linje från mitten av cirkeln till varje punkt, du bara delat att fjärdedel av cirkeln i tre lika delar. Se nedan…
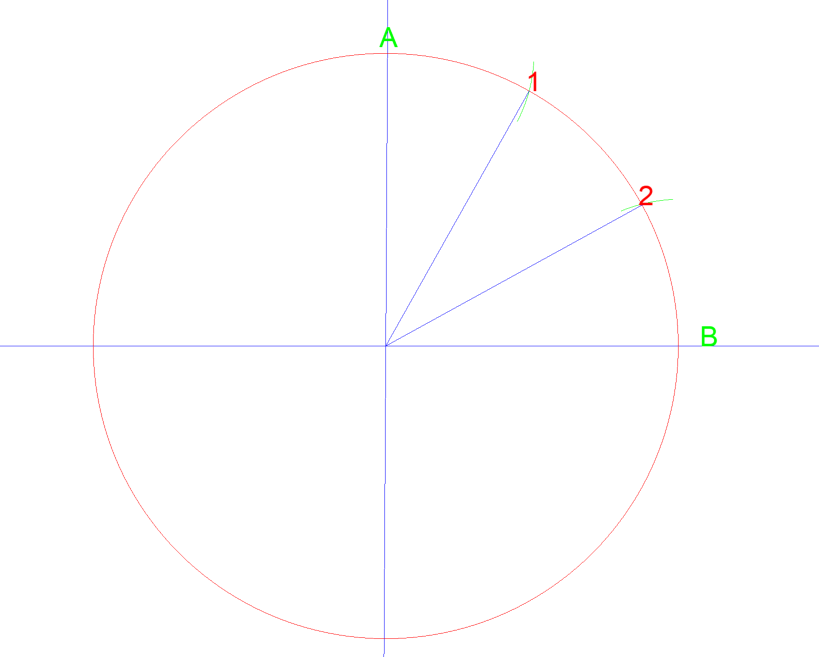
om du sedan gjorde det igen mellan A, 1, 2, & B kan du dela det kvartalet i en cirkel i 6 lika stora områden.
som vi täckte kort tidigare använder vi siffror för att hjälpa till med att ställa upp var linjer kommer att ansluta. Dessa linjer kommer att användas när vi sammanfogar två eller flera delar för att göra en montering. När vi fortsätter kommer du bättre att förstå hur detta numreringssystem fungerar.