FDTD and FDM algorithms for the MHOF analysis
a luz óptica é uma onda eletromagnética na natureza, e assim suas propriedades de propagação são regidas pelas leis da eletrodinâmica que são coletivamente conhecidas como equações de Maxwell. Sabe-se que a orientação de sinais de luz no MHOF com estruturas fotônicas de bandgap depende de um efeito de interferência construtiva devido à disposição periódica de buracos de ar idênticos. Por outro lado, quando os buracos de ar se tornam aleatórios em tamanho, localização, ou ambos, o fenômeno de reflexão interna total ocorre e a diferença de índice entre o núcleo e o revestimento fornece confinamento de luz e, portanto, orientação da luz ao longo da fibra. Embora as características de propagação de estruturas complicadas como MHOFs arbitrários não possam ser calculadas facilmente usando métodos analíticos, existem maneiras de resolver problemas eletromagnéticos numericamente.
In this section, two numerical techniques of finite-difference time-domain (FDTD) and finite difference method (FDM) are addressed considering extension to the analysis of holey optical fibers with arbitrary air-hole distributions. Cada uma destas técnicas tem certas vantagens. Usando o método FDTD, o campo eletromagnético contínuo em um volume finito de espaço é amostrado em pontos distintos em uma estrutura espacial e em pontos de amostragem igualmente espaçados no tempo. Os dados amostrados nos pontos são usados para cálculos numéricos de modos permitidos, sem gerar soluções de modo espúrio, em uma determinada guia de onda. Apesar de ser uma técnica eficaz para o cálculo de constantes de propagação de modos guiados, o método FDTD não é adequado para a avaliação de distribuições de campos de modo individual. Isto é porque a fonte é uma função de impulso no domínio do tempo cobrindo um espectro infinito, assim as soluções de distribuição de Campo São superposição de todos os modos possíveis. Para aliviar este problema com constantes de propagação disponíveis A partir de FDTD, distribuições de campos de modo individual são obtidas usando o FDM, que pode rápida e convenientemente fornecer soluções de campo de modo individual.
o FDTD ganhou popularidade considerável nos últimos anos, porque este método fornece soluções robustas, com base nas equações de Maxwell, e pode facilmente acomodar propriedades materiais de valor complexo. Um objeto material arbitrário pode ser aproximado construindo células unitárias para as quais as posições dos componentes de campo são eliminadas com os valores desejados de permitividade e permeabilidade. Uma vez que a geometria do objeto é especificada na região de simulação numérica, a condição fonte é modelada em algum lugar da região. Inicialmente, assume-se que todos os campos dentro do domínio de cálculo são identicamente zero. Em seguida, uma onda incidente é imposta para entrar na região de cálculo numérico.Usando o sistema MKS de unidades, vamos primeiro considerar as equações de curl de Maxwell expressas como::
onde ε é a permissividade elétrica constante de F/m e μ é a permeabilidade magnética constante em H/m. Expandindo a onda expressões e equacionar os componentes como, o sistema de seis acoplado de equações diferenciais parciais são formados para o FDTD análise da onda eletromagnética interações com o sistema geral de objetos tridimensionais. Note-se que os componentes do campo elétrico e magnético (Ex, Ey, Ez, Hx, Hy e Hz) são inter-relacionados. Ou seja, as equações de Maxwell não produzem diretamente valores de campo elétrico e magnético, mas sim relacionam a taxa de mudança entre valores de campo elétrico e magnético.
Adoção central finito diferença aproximação para o espaço e o tempo derivativos com precisão de segunda ordem, as seguintes aproximações como exemplos representativos em três dimensões (3D) FDTD formulação pode ser desenvolvido:
onde i, j, k e n são números inteiros para Δx, Δy, Δz, e Δt, respectivamente, como o espaço e incrementos de tempo .
uma vez que fibras ópticas como o MHOFs geralmente não têm variações ao longo da direção de propagação e variações das propriedades do material estão limitadas às direções transversais como mostrado na Figura 3, a formulação 3D do FDTD pode ser simplificada para o algoritmo bidimensional (2D) FDTD . Usando a notação fasor com a constante de propagação axial (β), Os derivados parciais de primeira ordem em relação a z são substituídos por-jß, porque a dependência z de Campos é como exp (- jßz). E dois campos adjacentes necessários para os derivados de primeira ordem na região do espaço discretizado podem ser representados por um campo no ponto médio entre eles. Com base nestes dois factos, a seguinte formulação, como exemplo, é obtido:
resultante 2D algoritmo tira vantagem de redução significativa no computador necessário a alocação de memória e tempo de execução. Assim, para o cálculo computacional de guias de ondas arbitrárias que são uniformes ao longo da direção de propagação de ondas, apenas a modelagem das seções transversais de guias de onda é suficiente.
junto com este algoritmo eficiente, meios infinitos no espaço 2D para um objeto eletromagnético arbitrário precisam ser modelados cuidadosamente, porque a memória de computador é limitada na região de cálculo, mesmo com tecnologia de corrente avançada. A fim de modelar regiões que se estendem para o infinito, uma camada perfeitamente compatível (LMP) como uma condição de limite de absorção altamente eficaz (ABC) é projetado no limite da estrutura externa de um domínio de cálculo. Idealmente, o meio absorvente é apenas tão espesso quanto algumas células de retículo, altamente absorvente, sem reflexo para todas as ondas impingindo, e eficaz ao longo de toda a gama de comprimentos de onda operacionais.
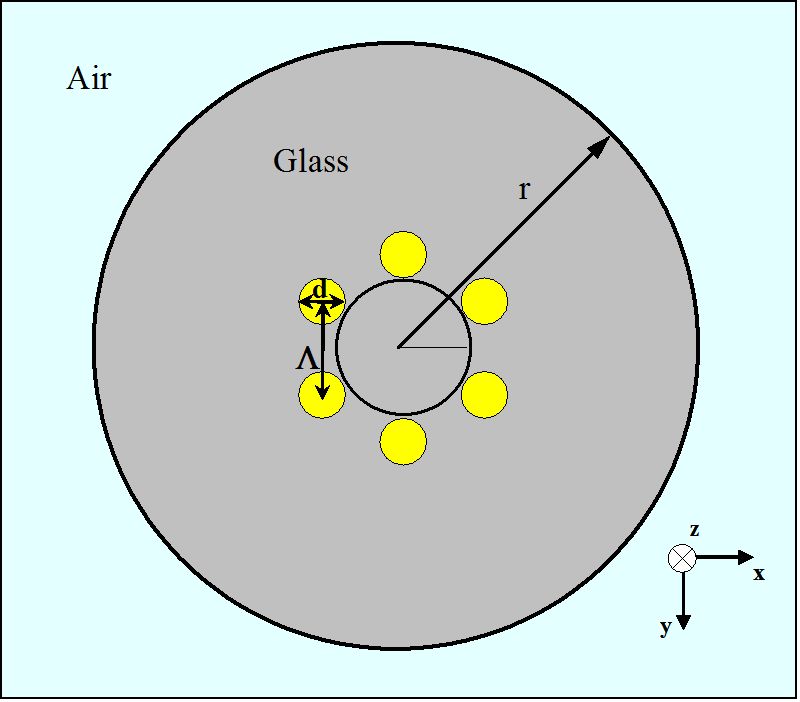
Figura 3.
esquemático de uma secção transversal para um MHOF com uma camada de orifícios de ar num arranjo hexagonal
Similarly to the development of the FDTD algorithm, the FDM formulation can be derived from the coupled Maxwell’s equations . Para as ondas contínuas em meios lineares e isotrópicos, a combinação de NQA (2) e (3) resulta na seguinte equação de onda vectorial:
where n is the refractive index and k0 is the propagation constant in free space. Muitos dispositivos de guarda-ondas, como fibras ópticas, podem ser vistos como Z-invariantes, ou estruturas Z-invariantes. Para essas estruturas,o índice de refração n(x,y, z) varia lentamente ao longo da direção de propagação z, que é válida para a maioria dos dispositivos de ondas guiadas fotônicas. Utilizando o vetor de identidade de∇×∇×=∇(∇⋅)−∇2, Eq. (8) pode ser escrito como
Também com a suposição razoável de insignificante dependência de tempo ao longo do eixo z, o FDM formulação como na equação (9) pode ser implementada substituindo espaciais derivados com diferença finito aproximações. Note-se que o componente transversal de (9) é
em que o subscrito “t” representa os componentes transversais. Uma vez que a componente longitudinal pode ser facilmente obtida por aplicação da seguinte restrição de divergência zero (Lei de Gauss) :
os componentes transversais são suficientes para descrever a natureza vectorial completa do campo electromagnético numa guia de ondas óptica.
para a investigação inicial das propriedades de orientação de MHOFs, a fibra óptica mostrada na Figura 3 é analisada por computador. Geralmente, a geometria MHOF pode ser descrita com dois parâmetros, comprimento de passo (Λ) e diâmetro (d), como indicado na Figura 3. Aqui, o comprimento do passo é a distância entre os centros de dois buracos de ar mais próximos com a forma cilíndrica. Para o MHOF da Figura 3, cada pequeno orifício de ar tem um diâmetro de 1,4 µm, constituindo um hexágono Com Λ = 1,7 µm. A porção de vidro em torno dos seis buracos de ar das regiões Amarelas tem um índice de refração de 1,45. Presume-se que o raio exterior (r) da fibra holográfica é de 10 µm. Além disso, a região externa do MHOF é o ar.
uma Vez que a seção transversal de um holey fibra é definido em um bom domínio de cálculo, o FDTD simulação pode ser realizada com vários parâmetros especificados, tais como τ na definição de uma Gaussiana de origem, Δt estável de simulação, o número total (ntot) de passos de tempo para a amostragem de dados no domínio do tempo, e razoáveis valores de β. Aqui, a fim de evitar divergências numéricas e assegurar a estabilidade do algoritmo FDTD, é necessário seleccionar um Δt adequado para satisfazer as seguintes condições de estabilidade::
em que cM é a velocidade máxima da fase de onda num dado modelo numérico. Resumindo o mecanismo por trás da análise FDTD, a simulação por computador segue as seguintes etapas:
-
Escolha valores de parâmetro (τ, Δt, ntot, e β)
-
Dados de amostragem de um componente de campo no domínio do tempo.
-
Tomar a transformada de Fourier dos dados de tempo
-
Obter dados espectrais de um componente de campo
-
Escolha o modo de freqüências associado com o valor de β
-
Recolher β e o modo de frequência de dados
-
Faça um gráfico do modo de índice versus comprimento de onda
a Figura 4 ilustra as curvas características, que são obtidos a partir do FDTD cálculo, para os três primeiros modos inferiores do MHOF definidos na Figura 3.
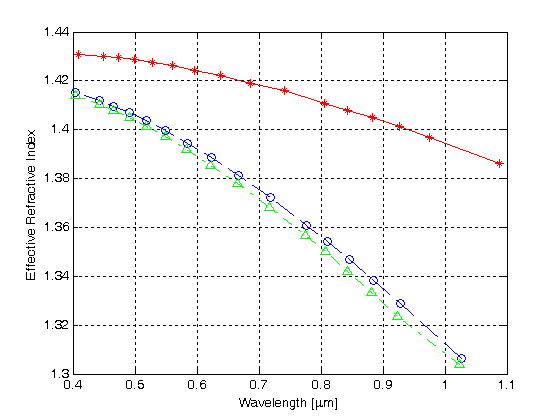
Figura 4.
Eficaz índice de refração versus comprimento de onda para os três primeiros modos de um MHOF com uma camada de buracos de ar
A curva vermelha com a estrela símbolos parcelas normalizados de propagação constante para o primeiro modo versus comprimento de onda, enquanto que o azul e o verde curvas mostram o normalizada de propagação de constantes para o segundo e o terceiro modos, respectivamente. The results indicate that the HMOF with a single hexagonal air-hole cladding layer supports multimode guiding.