de Acordo com Noam Chomosky, existem quatro tipos de gramáticas de Tipo 0, tipo 1, Tipo 2 e Tipo 3. A tabela a seguir mostra como eles diferem um do outro−
| Gramática de Tipo | Gramática Aceito | Idioma Aceito | Automaton |
|---|---|---|---|
| Digite 0 | gramática Irrestrita | Recursivamente enumerável idioma | Máquina de Turing |
| Digite 1 | sensível ao Contexto gramatical | contextual idioma | Linear limitado automaton |
| Tipo 2 | gramática livre de Contexto | livre de Contexto idioma | Pushdown automaton |
| Tipo 3 | gramática Regular | linguagem Regular | Finite state automaton |
dê uma olhada na ilustração a seguir. Ele mostra o escopo de cada tipo de gramática −
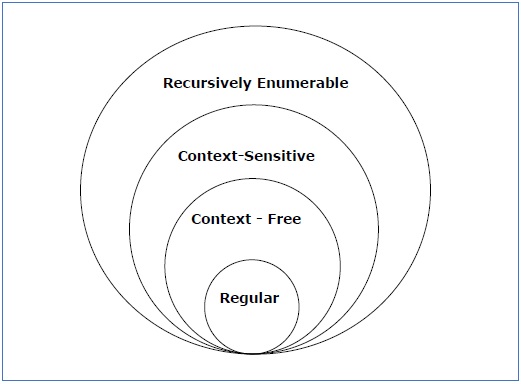
Gramática Tipo – 3
gramáticas Tipo-3 geram linguagens regulares. As gramáticas do tipo 3 devem ter um único não-terminal no lado esquerdo e um lado direito constituído por um único terminal ou um único terminal seguido por um único não-terminal.
the productions must be in the form X → A or X → aY
where X, Y ∈ N (Non terminal)
and a ∈ T (Terminal)
The rule s → ε is allowed if S does not appear on the right side of any rule.
exemplo
X → ε X → a | aYY → b
Gramática tipo – 2
gramáticas tipo-2 geram linguagens livres de contexto.
As produções devem ser na forma A → γ
onde A ∈ N (Não terminal)
e γ ∈ (T ∪ N)* (Cadeia de terminais e não-terminais).
estas linguagens geradas por estas gramáticas são reconhecidas por um autômato pushdown não-determinístico.
exemplo
S → X a X → a X → aX X → abc X → ε
Gramática tipo – 1
gramáticas tipo-1 geram linguagens sensíveis ao contexto. As produções devem ter o formato:
α β → α γ β
onde A ∈ N (Não-terminal)
e α, β, γ ∈ (T ∪ N)* (Cadeias de terminais e não-terminais)
As cadeias α e β podem ser vazio, mas, γ deve ser não vazio.
the rule s → ε is allowed if S does not appear on the right side of any rule. As linguagens geradas por estas gramáticas são reconhecidas por um autômato linearmente limitado.
exemplo
AB → AbBc A → bcA B → b
Gramática Tipo – 0
gramáticas Tipo-0 geram linguagens recursivamente enumeráveis. As produções não têm restrições. Eles são qualquer gramática de estrutura de fase, incluindo todas as gramáticas formais.
eles geram as linguagens que são reconhecidas por uma máquina de Turing.
as produções podem ser na forma de α → β onde α é uma cadeia de terminais e não terminais com pelo menos um não-terminal e α Não pode ser nulo. β é uma cadeia de terminais e não-terminais.Exemplo
S → ACaB Bc → acB CB → DB aD → Db