het catamorfisme voor beide is een veralgemening van zijn vouw. Het catamorfisme maakt bewerkingen mogelijk die niet beschikbaar zijn via fold.
dit artikel maakt deel uit van een serie artikelen over catamorfismen. Een catamorfisme is een universele abstractie die beschrijft hoe een gegevensstructuur te verteren in een potentieel compactere waarde.
dit artikel geeft de catamorfie voor beide (ook bekend als resultaat), evenals hoe het te identificeren. Het begin van dit artikel presenteert het catamorfisme in C#, met voorbeelden. De rest van het artikel beschrijft hoe je het catamorfisme kunt afleiden. Dit deel van het artikel presenteert mijn werk in Haskell. Lezers die zich niet op hun gemak voelen met Haskell kunnen gewoon het eerste deel lezen en de rest van het artikel als een optionele bijlage beschouwen.
ofwel is een gegevenscontainer die twee elkaar uitsluitende resultaten modelleert. Het wordt vaak gebruikt om waarden te retourneren die ofwel correct (rechts), of onjuist (links) kunnen zijn. In statisch getypte functionele programmering met een voorkeur voor totale functies, ofwel biedt een saner, meer redelijke manier om succes en fout resultaten te modelleren dan het gooien van uitzonderingen.
C # catamorfisme #
dit artikel Gebruikt de Kerkcodering van beide. Het catamorfisme voor beide is de Match methode:
T Match<T>(Func<L, T> onLeft, Func<R, T> onRight);
tot Dit artikel zijn alle voorgaande catamorfismen een paar gemaakt van een beginwaarde en een functie. Het beide catamorfisme is een generalisatie, omdat het een paar functies is. Een functie behandelt het geval waar er een linker waarde is, en de andere functie behandelt het geval waar er een rechter waarde is. Beide functies moeten hetzelfde, unifying type retourneren, wat vaak een string of iets dergelijks is die in een gebruikersinterface kan worden weergegeven:
> IEither<TimeSpan, int> e = new Left<TimeSpan, int>(TimeSpan.FromMinutes(3));> e.Match(ts => ts.ToString(), i => i.ToString())"00:03:00"> IEither<TimeSpan, int> e = new Right<TimeSpan, int>(42);> e.Match(ts => ts.ToString(), i => i.ToString())"42"
u zult vaak voorbeelden zien zoals het bovenstaande dat zowel links als rechts gevallen verandert in strings of iets dat kan worden weergegeven als een verenigende reactie type, maar dit is op geen enkele manier vereist. Als u met een verenigend type kunt komen, kunt u beide gevallen naar dat type converteren:
> IEither<Guid, string> e = new Left<Guid, string>(Guid.NewGuid());> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)12> IEither<Guid, string> e = new Right<Guid, string>("foo");> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)3
in de twee bovenstaande voorbeelden gebruikt u twee verschillende functies die beide respectievelijk Guid en string waarden reduceren tot een getal. De functie die Guid waarden omzet in een getal telt hoeveel hexadecimale cijfers groter of gelijk zijn aan A (10). De andere functie geeft gewoon de lengte van de string terug, als deze er is. Dat voorbeeld heeft weinig zin, maar de Match methode geeft daar niets om.
in de praktijk wordt beide vaak gebruikt voor foutafhandeling. Het artikel over de Kerkcodering van beide bevat een voorbeeld.
ofwel F-Algebra #
zoals in het vorige artikel, zal ik Fix en cata gebruiken zoals uitgelegd in Bartosz Milewski ’s uitstekende artikel over F-algebra’ s.
terwijl F-algebra ‘ s en vaste punten meestal worden gebruikt voor recursieve datastructuren, kunt u ook een F-Algebra definiëren voor een niet-recursieve datastructuur. Je zag daar al een voorbeeld van in de artikelen over Booleaans catamorfisme en misschien catamorfisme. Het verschil tussen bijvoorbeeld misschien waarden en een van beide is dat beide gevallen van een van beide een waarde dragen. U kunt dit modelleren als een Functor met zowel een dragertype als twee typeargumenten voor de gegevens die beide kunnen bevatten:
data EitherF l r c = LeftF l | RightF r deriving (Show, Eq, Read) instance Functor (EitherF l r) where fmap _ (LeftF l) = LeftF l fmap _ (RightF r) = RightF r
ik koos ervoor om de ‘gegevenstypen’ l (voor links) en r (voor rechts) aan te roepen, en het carriertype c (voor carrier). Zoals ook het geval was met BoolF en MaybeF, negeert het Functor – exemplaar de kaartfunctie omdat het dragertype ontbreekt in zowel het LeftF – geval als het RightF – geval. Net als de Functor instanties voor BoolF en MaybeF lijkt het erop dat er niets gebeurt, maar op het type niveau is dit nog steeds een vertaling van EitherF l r c naar EitherF l r c1. Niet veel van een functie, misschien, maar zeker een endofunctor.
zoals ook het geval was bij het afleiden van de Misschien-en Lijstcatamorfismen, is Haskell niet blij met het definiëren van instanties voor een type als Fix (EitherF l r). Om dat probleem aan te pakken, kunt u een newtype wrapper invoeren:
newtype EitherFix l r = EitherFix { unEitherFix :: Fix (EitherF l r) } deriving (Show, Eq, Read)
u kunt definiëren Functor, Applicative, Monad, enz. instanties voor dit type zonder toevlucht te nemen tot een funky GHC extensies. Houd in gedachten dat uiteindelijk, het doel van al deze code is gewoon om erachter te komen hoe de catamorfisme eruit ziet. Deze code is niet bedoeld voor daadwerkelijk gebruik.
een paar helperfuncties maken het gemakkelijker om EitherFix waarden te definiëren:
leftF :: l -> EitherFix l rleftF = EitherFix . Fix . LeftF rightF :: r -> EitherFix l rrightF = EitherFix . Fix . RightF
met deze functies kunt u EitherFix waarden aanmaken:
Prelude Data.UUID Data.UUID.V4 Fix Either> leftF <$> nextRandomEitherFix {unEitherFix = Fix (LeftF e65378c2-0d6e-47e0-8bcb-7cc29d185fad)}Prelude Data.UUID Data.UUID.V4 Fix Either> rightF "foo"EitherFix {unEitherFix = Fix (RightF "foo")}
dat is alles wat je nodig hebt om het catamorfisme te identificeren.
Haskell-catamorfisme #
op dit punt heb je twee van de drie elementen van een F-Algebra. U heeft een endofunctor (EitherF l r) en een object c, maar u moet nog steeds een morfisme EitherF l r c -> cvinden. Merk op dat de algebra die je moet vinden de functie is die de functor reduceert tot zijn dragertype c, niet de ‘gegevenstypen’ l en r. Het is even wennen, maar zo werken catamorfismen. Dit betekent echter niet dat u l en r kunt negeren, zoals u zult zien.
zoals in de vorige artikelen, begin met het schrijven van een functie die het catamorfisme zal worden, gebaseerd op cata:
eitherF = cata alg . unEitherFix where alg (LeftF l) = undefined alg (RightF r) = undefined
hoewel dit compileert, met zijn undefined implementaties, doet het duidelijk niets nuttigs. Ik vind echter dat het me helpt te denken. Hoe kunt u een waarde van het type c retourneren uit de zaak LeftF? U kunt een argument doorgeven aan de functie eitherF :
eitherF fl = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = undefined
hoewel u technisch gezien een argument van het type c zou kunnen doorgeven aan eitherF en dan die waarde zou kunnen retourneren uit het geval LeftF, zou dat betekenen dat u de waarde l zou negeren. Dit zou onjuist zijn, dus maak in plaats daarvan het argument een functie en noem het met l. Ook kunt u het RightF geval op dezelfde manier behandelen:
eitherF :: (l -> c) -> (r -> c) -> EitherFix l r -> ceitherF fl fr = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = fr r
dit werkt. Aangezien cata het type Functor f => (f a -> a) -> Fix f -> a heeft, betekent dit dat alg het type f a -> aheeft. In het geval van EitherF leidt de compiler af dat de functie alg het type EitherF l r c -> c heeft, wat precies is wat je nodig hebt!
u kunt nu zien waarvoor het dragertype c dient. Het is het type dat de algebra extraheert, en dus het type dat het catamorfisme retourneert.
dit is dus het catamorfisme voor beide. Zoals tot nu toe consistent is geweest, is het een paar, maar nu gemaakt van twee functies. Zoals u herhaaldelijk hebt gezien, is dit niet de enige mogelijke catamorfose, omdat u bijvoorbeeld de argumenten triviaal kunt omdraaien naar eitherF.
ik heb de hier getoonde representatie gekozen omdat deze isomorf is met de either functie van Haskell ‘ s ingebouwde Data.Either module, die de functie De “Case analysis for the Either type”noemt. Beide functies (eitherF en either) zijn equivalent aan de bovenstaande methode C# Match.
Basis #
u kunt de meeste andere nuttige functionaliteit implementeren met eitherF. Hier is de Bifunctor instantie:
instance Bifunctor EitherFix where bimap f s = eitherF (leftF . f) (rightF . s)
uit deze instantie volgt de instantie Functor triviaal:
instance Functor (EitherFix l) where fmap = second
bovenop Functor kunt u Applicativetoevoegen:
instance Applicative (EitherFix l) where pure = rightF f <*> x = eitherF leftF (<$> x) f
merk op dat de <*> implementatie vergelijkbaar is met de <*> implementatie voor MaybeFix. Hetzelfde geldt voor de instantie Monad :
instance Monad (EitherFix l) where x >>= f = eitherF leftF f x
niet alleen is EitherFix Foldable, het is Bifoldable:
instance Bifoldable EitherFix where bifoldMap = eitherF
merk op dat bifoldMap identiek is aan eitherF.
de instantie Bifoldable stelt u in staat om de instantie Foldable triviaal te implementeren:
instance Foldable (EitherFix l) where foldMap = bifoldMap mempty
u kunt de aanwezigheid van mempty verwarrend vinden, omdat bifoldMap (of eitherF; ze zijn identiek) twee functies als argument neemt. Is mempty een functie?
Ja, mempty kan een functie zijn. Hier is het. Er is een Monoid instantie voor elke functie a -> m, waarbij m een Monoid instantie is, en mempty de identiteit is voor die monoïde. Dat is de instantie die hier wordt gebruikt.
net zoals EitherFix Bifoldable is, is het ook Bitraversable:
instance Bitraversable EitherFix where bitraverse fl fr = eitherF (fmap leftF . fl) (fmap rightF . fr)
u kunt gemakkelijk de Traversable instantie implementeren op basis van de Bitraversable instantie:
instance Traversable (EitherFix l) where sequenceA = bisequenceA . first pure
tot slot kunt u conversies van en naar het standaard Either type implementeren, met ana als de duale van cata:
toEither :: EitherFix l r -> Either l rtoEither = eitherF Left Right fromEither :: Either a b -> EitherFix a bfromEither = EitherFix . ana coalg where coalg (Left l) = LeftF l coalg (Right r) = RightF r
dit toont aan dat EitherFix isomorf is aan Either, wat weer aantoont dat eitherF en either gelijkwaardig zijn.
relaties #
in deze serie heb je verschillende voorbeelden gezien van catamorfismen van structuren die geen plooien hebben, catamorfismen die samenvallen met plooien, en nu een catamorfisme dat algemener is dan de plooi. De inleiding tot de serie bevat dit diagram:
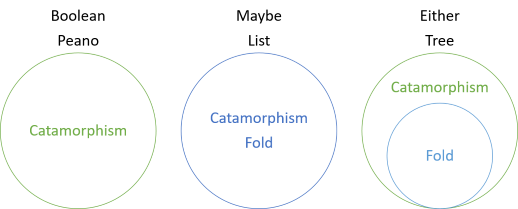
dit toont aan dat Booleaanse waarden en Peano-getallen catamorfismen hebben, maar geen vouwen, terwijl Voor misschien en lijst de vouw en het catamorfisme hetzelfde zijn. Voor beide is de vouw echter een speciaal geval van het catamorfisme. De vouw voor beide ‘pretendeert’ dat de linkerkant niet bestaat. In plaats daarvan wordt de linkerwaarde geïnterpreteerd als een ontbrekende rechterwaarde. Dus, om beide waarden te vouwen, moet u een ‘fallback’ waarde die zal worden gebruikt in het geval een van beide waarde is niet een juiste waarde:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e""
In een GHCi sessie zoals hierboven, kunt u twee waarden van hetzelfde type maken. De rechter case is een Ordering waarde, terwijl de linker case een Integer waarde is.
met foldr is er geen manier om toegang te krijgen tot de linkercase. Terwijl u de juiste waarde Ordering kunt openen en transformeren, wordt het getal 42 gewoon genegeerd tijdens de vouw. In plaats daarvan wordt de standaardwaarde "" geretourneerd.
contrasteert dit met het catamorfisme, dat beide gevallen kan benaderen:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"42"
In een sessie als deze herschept u dezelfde waarden, maar met het catamorfisme eitherF kunt u nu zowel de linker-als de rechter cases openen en transformeren. Met andere woorden, het catamorfisme stelt u in staat om bewerkingen uit te voeren die niet mogelijk zijn met de vouw.
het is echter interessant om op te merken dat hoewel de vouw een specialisatie is van het catamorfisme, de bifold identiek is aan het catamorfisme.
samenvatting #
het catamorfisme voor beide is een paar functies. Een functie transformeert de linker behuizing, terwijl de andere functie de rechter behuizing transformeert. Voor elke waarde wordt slechts één van deze functies gebruikt.
toen ik oorspronkelijk het concept van een catamorfisme tegenkwam, vond ik het moeilijk om onderscheid te maken tussen catamorfisme en vouwen. Mijn probleem was, denk ik, dat de tutorials die ik tegenkwam meestal gelinkte lijsten gebruikten om aan te tonen hoe, in dat geval, de vouw het catamorfisme is. Het blijkt echter dat dit niet altijd het geval is. Een catamorfisme is een algemene abstractie. Een vouw, aan de andere kant, lijkt mij vooral gerelateerd aan collecties.
In dit artikel zag je het eerste voorbeeld van een catamorfisme dat meer kan doen dan de vouw. Voor beide is de vouw slechts een speciaal geval van het catamorfisme. Je zag echter ook hoe de catamorfie identiek was aan de bifold. Het is dus nog steeds niet helemaal duidelijk hoe deze concepten zich verhouden. Daarom, in het volgende artikel, krijg je een voorbeeld van een container waar er geen bifold, en waar de catamorfisme is, inderdaad, een veralgemening van de vouw.
volgende: Boomkatamorfisme.