엑셀 스프레드시트에서 클러스터 분석을 처음부터 끝까지 실행하는 방법에 대한 단계별 가이드입니다. 이 웹 사이트에서 무료로 다운로드 할 수있는 클러스터 분석을 자동으로 실행하는 엑셀 템플릿이 있습니다. 그러나 당신이 케이를 실행하는 방법을 알고 싶다면-자신을 엑셀에 클러스터링을 의미,다음이 문서는 당신을위한 것입니다.
이 문서뿐만 아니라,나는 또한 엑셀에서 클러스터 분석을 실행하는 방법의 비디오 워크를 통해 있습니다.
1 단계–데이터 세트로 시작
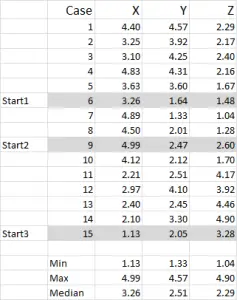
그림 1
이 예에서는 15 개의 사례(또는 응답자)를 사용하고 있습니다.이 예에서는 세 가지 변수에 대한 데이터가 있습니다.
이 예에서는 데이터가 1–5 로 조정된다는 것을 알아야합니다. 귀하의 데이터는 명목상의 데이터 척도를 제외한 모든 형태 일 수 있습니다(사용할 데이터의 기사 참조).
참고:확장 된 데이터를 사용하는 것을 선호하지만 필수는 아닙니다. 그 이유는 특이치를”포함”하기 때문입니다. 예를 들어,소득 데이터(인구 통계 학적 측정)를 사용하고 있습니다.대부분의 데이터는 약$40,000 에서$100,000 정도이지만 소득이 500 만 달러 인 사람이 있습니다.그 사람을”$250,000 이상”소득 브래킷과 소득 1-9 규모로 분류하는 것이 더 쉽습니다.하지만 작업중인 데이터에 따라 다릅니다.
이 예제에서 세 가지 시작 위치가 강조 표시되었음을 확인할 수 있습니다.
2 단계–두 변수 경우,엑셀에 분산 그래프를 사용
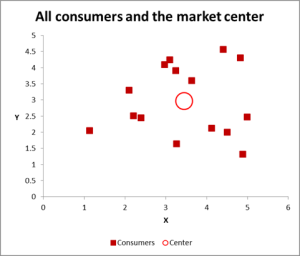
그림 2
이 군집 분석 예제에서는 세 가지 변수를 사용하고 있지만 군집할 변수가 두 개만 있는 경우 분산형 차트를 시작하는 것이 좋습니다. 그리고 때로는 시각적 수단을 통해 데이터를 클러스터링 할 수 있습니다.
이 분산 형 그래프에서 볼 수 있듯이 각 개별 사례(이 예에서 소비자라고 부르는 것)가 모든 사례(빨간색 원)의 평균(평균)과 함께 매핑되었습니다.
데이터/그래프를 보는 방법에 따라 여러 개의 클러스터가 나타납니다. 이 경우 다음 차트와 같이 비교적 별개의 클러스터 3 개 또는 4 개를 식별할 수 있습니다.
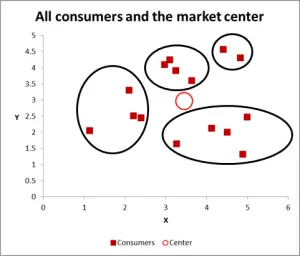
그림 3
이 다음 그래프를 통해 가능한 클러스터를 눈에 띄게 확인하고 동그라미를 그렸습니다. 내가 제안한 바와 같이,고려해야 할 두 가지 변수가있을 때 좋은 접근 방식–하지만이 경우 우리는 세 가지 변수가(그리고 당신은 더 많은 것을 가질 수 있습니다),그래서이 시각적 접근 방식은 기본 데이터 세트에 대해서만 작동합니다–이제 엑셀 계산을 수행하는 방법을 살펴 보겠습니다 케이-클러스터링을 의미합니다.
3 단계-각 데이터 포인트에서 클러스터 중심까지의 거리 계산
이 워크 스루 예제에서는 세 개의 세그먼트/클러스터 만 식별하려고한다고 가정합니다. 예,위의 다이어그램에서 네 개의 클러스터가 분명하지만 두 개의 변수 만 보입니다. 당신이 원하는만큼 클러스터를 식별하기 위해이 엑셀 방법을 사용할 수 있습니다–아래에 설명 된대로 그냥 같은 개념을 따르십시오.
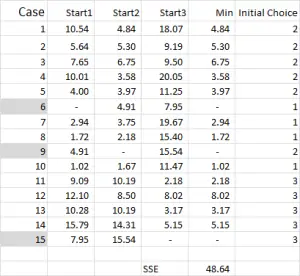
그림 4
케이-의미 클러스터링 일반적으로 분석을 시작하기 위해 임의의 사례(시작점 또는 시드)를 선택합니다.
이 예에서-세 개의 클러스터를 만들고 싶으므로 세 개의 시작점이 필요합니다. 이러한 시작 지점에 대해 6,9 및 15 경우를 선택했지만 임의의 점도 적합 할 수 있습니다.
이러한 경우를 선택한 이유는 변수 만 볼 때 사례 6 이 중앙값이고 사례 9 가 최대 값이고 사례 15 가 최소값이기 때문입니다. 이것은이 세 가지 경우가 서로 다소 다르다는 것을 암시하며,확산되기 때문에 출발점이 좋습니다.
클러스터 분석이 때때로 다른 결과를 생성하는 이유에 대한 기사를 참조하십시오.
테이블 출력을 참조–이 엑셀에서 우리의 첫 번째 계산이며 클러스터의 우리의”초기 선택”을 생성합니다. 시작 1 은 사례 6 의 데이터이고 시작 2 는 사례 9 이고 시작 3 은 사례 15 입니다. 이 각각의 교차점은 테이블에 0(-)을 제공한다는 점에 유의해야합니다.
계산은 어떻게 작동합니까?
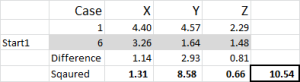
그림 5
테이블의 첫 번째 숫자를 살펴 보겠습니다-사례 1,시작 1=10.54.
임의로 케이스 6 을 클러스터 1 의 임의의 시작점으로 지정했음을 기억하십시오. 우리는 거리를 계산하려면 우리는 제곱 방법의 합을 사용-여기에 도시 된 바와 같이. 집합의 세 데이터 요소 각각의 차이를 계산 한 다음 차이를 제곱 한 다음 합계를 계산합니다.
우리는 여기에 표시된 것처럼”기계적으로”할 수 있습니다.
그림 4 를 다시 참조하면 세 가지 시작점 각각에서 각 케이스의 최소 거리를 찾을 수 있습니다.이 거리는 케이스가 가장 가까운 클러스터(1,2 또는 3)를 알려줍니다.이 클러스터는’초기 선택 열’에 표시됩니다.
4 단계-각 클러스터 세트의 평균(평균)계산
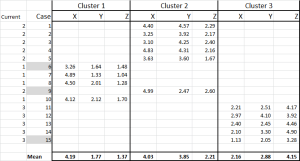
그림 6
우리는 이제 초기 클러스터에 각각의 경우를 할당 한-우리는 테이블에 경우 문을 사용하여 그 배치 할 수 있습니다(그림 6 에 도시 된 바와 같이).
표 아래쪽에는 이러한 각 경우의 평균(평균)이 있습니다. 하나의”대표”데이터 포인트에 의존하는 대신 각각을 나타내는 일련의 사례가 있습니다.
5 단계-반복 3 단계–개정 평균으로부터의 거리
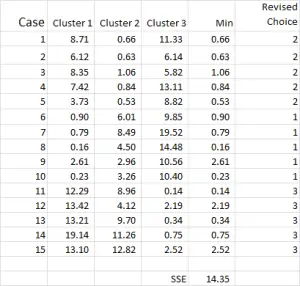
그림 7
클러스터 분석 프로세스는 이제 클러스터가 안정화 될 때까지 4 단계와 5 단계(반복)를 반복하는 문제가됩니다.
각 클러스터에 대해 수정된 평균을 사용할 때마다. 따라서 그림 7 은 두 번째 반복을 보여 주지만 이번에는 그림 1 의 시작 지점 대신 그림 6 의 맨 아래에 생성 된 수단을 사용하고 있습니다.
이제 클러스터 응용 프로그램에 약간의 변화가 있었으며 사례 9(시작 지점 중 하나)가 다시 할당되었음을 확인할 수 있습니다.
아래쪽에서 계산된 오차 제곱의 합을 볼 수도 있습니다. 우리의 목표는 이제 4 단계와 5 단계를 반복하여 최소한의 개선 만 표시하거나 각 반복에서 클러스터 할당 변경이 미미할 때까지 반복하는 것입니다.
최종 단계–클러스터 그래프 및 요약
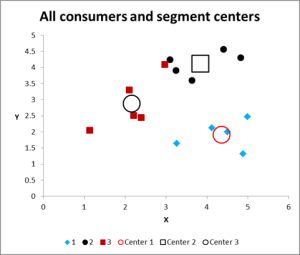
그림 8
여러 반복을 실행 한 후,우리는 지금 그래프와 데이터를 요약 할 수있는 출력을 가지고있다.
이 클러스터 분석 엑셀 예제에 대한 출력 그래프입니다.
보시다시피,각 클러스터의 중심(평균)과 함께 세 개의 별개의 클러스터가 표시됩니다.
필요한 경우 우리는 또한 우리가 엑셀에서 그것을 밖으로 일한 테이블 형태로이 데이터를 표시 할 수 있습니다.
그래프의 상단 중앙의 검은 점 바로 옆에있는 작은 빨간색 사각형 인 클러스터 3 의 경우를 살펴보십시오. 이 경우는 세 번째 변수의 영향 때문에 거기에 있으며,이 두 변수 차트에는 표시되지 않습니다.