어느 쪽의 이형성 어느 쪽의 이형성은 그 배의 일반화이다. 이 변형은 접기를 통해 사용할 수없는 작업을 가능하게합니다.
이 기사는 이형성에 관한 기사 시리즈의 일부입니다. 이형성은 데이터 구조를 잠재적으로 더 컴팩트 한 값으로 다이제스트하는 방법을 설명하는 보편적 추상화입니다.
이 기사는 둘 중 하나(결과라고도 함)에 대한 이형성과 그것을 식별하는 방법을 제시합니다. 이 기사의 시작 부분에는 다음과 같은 예가 나와 있습니다. 이 기사의 나머지 부분에서는 이형성을 추론하는 방법을 설명합니다. 이 기사의이 부분은 하스켈에서 내 작품을 제시합니다. 하스켈에 익숙하지 않은 독자는 첫 번째 부분을 읽고 나머지 기사를 선택적 부록으로 간주 할 수 있습니다.
둘 중 하나는 두 개의 상호 배타적 결과를 모델링하는 데이터 컨테이너입니다. 올바른(오른쪽)또는 잘못된(왼쪽)값을 반환하는 데 자주 사용됩니다. 총 함수에 대한 선호도를 가진 정적으로 형식화 된 함수형 프로그래밍에서는 예외를 던지는 것보다 성공 및 오류 결과를 모델링하는 더 안전하고 합리적인 방법을 제공합니다.
다#이형성#
이 기사는 두 가지 중 하나의 교회 인코딩을 사용합니다. 둘 중 하나에 대한 이형성은Match방법입니다.:
T Match<T>(Func<L, T> onLeft, Func<R, T> onRight);
이 기사까지 이전의 모든 변형은 초기 값과 함수로 만든 쌍이었습니다. 이 두 가지 변형은 한 쌍의 함수이기 때문에 일반화입니다. 한 함수는 왼쪽 값이 있는 경우를 처리하고 다른 함수는 오른쪽 값이 있는 경우를 처리합니다. 두 함수 모두 동일한 통합 형식을 반환해야 합니다.:
> IEither<TimeSpan, int> e = new Left<TimeSpan, int>(TimeSpan.FromMinutes(3));> e.Match(ts => ts.ToString(), i => i.ToString())"00:03:00"> IEither<TimeSpan, int> e = new Right<TimeSpan, int>(42);> e.Match(ts => ts.ToString(), i => i.ToString())"42"
당신은 종종 문자열 또는 통합 응답 유형으로 표현 될 수있는 무언가로 왼쪽과 오른쪽 케이스를 모두 회전 위와 같은 예제를 볼 수 있지만,이 방법이 필요하지 않습니다. 통합 형식을 사용할 수 있는 경우 두 경우를 모두 해당 형식으로 변환할 수 있습니다:
> IEither<Guid, string> e = new Left<Guid, string>(Guid.NewGuid());> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)12> IEither<Guid, string> e = new Right<Guid, string>("foo");> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)3
위의 두 예제에서는 각각Guid와string값을 숫자로 줄이는 두 개의 서로 다른 함수를 사용합니다. Guid값을 숫자로 바꾸는 함수는(10)보다 크거나 같은 16 진수의 수를 계산합니다. 이 경우 다른 함수는 단순히string의 길이를 반환합니다. 이 예제는 거의 의미가 없지만Match방법은 신경 쓰지 않습니다.
실제 사용에서는 오류 처리에 자주 사용됩니다. 둘 중 하나의 교회 인코딩에 대한 기사에는 예가 포함되어 있습니다.이전 기사에서와 같이,나는Fix와cata를 바토시 밀레프스키의 훌륭한 기사 에프-대수에 대한 설명으로 사용할 것이다.
에프-대수 및 고정점은 주로 재귀 데이터 구조에 사용되지만 비 재귀 데이터 구조에 대한 에프-대수를 정의 할 수도 있습니다. 당신은 이미 부울 이형성과 어쩌면 이형성에 관한 기사에서 그 예를 보았습니다. 예를 들어 어쩌면 값과 둘 중 하나의 차이는 두 경우 모두 값을 가지고 있다는 것입니다. 이를Functor로 모델링하여 캐리어 형식과 둘 중 하나에 포함될 수 있는 데이터에 대한 두 가지 형식 인수를 모두 사용할 수 있습니다:
data EitherF l r c = LeftF l | RightF r deriving (Show, Eq, Read) instance Functor (EitherF l r) where fmap _ (LeftF l) = LeftF l fmap _ (RightF r) = RightF r
‘데이터 유형’l(왼쪽)및r(오른쪽)및 캐리어 유형c(캐리어)을 호출하기로 결정했습니다. BoolF및MaybeF의 경우와 마찬가지로Functor인스턴스는LeftF사례와RightF사례 모두에서 캐리어 유형이 없기 때문에 맵 기능을 무시합니다. BoolF및MaybeF에 대한Functor인스턴스와 마찬가지로 아무 일도 일어나지 않는 것처럼 보이지만 유형 수준에서는 여전히EitherF l r c에서EitherF l r c1로 번역 된 것입니다. 아마도 많은 기능은 아니지만 확실히 엔도 기능.
어쩌면 목록 이형성을 추론 할 때도 마찬가지로 하스켈은Fix (EitherF l r)와 같은 유형의 인스턴스를 정의하는 데 너무 만족하지 않습니다. 이 문제를 해결하기 위해newtype래퍼를 도입 할 수 있습니다:
newtype EitherFix l r = EitherFix { unEitherFix :: Fix (EitherF l r) } deriving (Show, Eq, Read)
다음을 정의 할 수 있습니다Functor, Applicative, Monad, 기타 이 유형의 인스턴스는 펑키 한 확장 기능을 사용하지 않고 사용할 수 있습니다. 궁극적으로,이 모든 코드의 목적은 단지 이형성이 어떻게 생겼는지 알아내는 것입니다. 이 코드는 실제 사용을 위한 것이 아닙니다.
도우미 함수 쌍을 사용하면EitherFix값을 쉽게 정의할 수 있습니다.:
leftF :: l -> EitherFix l rleftF = EitherFix . Fix . LeftF rightF :: r -> EitherFix l rrightF = EitherFix . Fix . RightF
이러한 함수를 사용하면EitherFix값을 만들 수 있습니다:
Prelude Data.UUID Data.UUID.V4 Fix Either> leftF <$> nextRandomEitherFix {unEitherFix = Fix (LeftF e65378c2-0d6e-47e0-8bcb-7cc29d185fad)}Prelude Data.UUID Data.UUID.V4 Fix Either> rightF "foo"EitherFix {unEitherFix = Fix (RightF "foo")}
즉,이형성을 식별 할 필요가 전부입니다.
하스켈 이형성#
이 시점에서,당신은 에프 대수의 세 가지 요소 중 두 가지가 있습니다. 엔도 펑터(EitherF l r)와 객체c가 있지만 여전히 형태EitherF l r c -> c를 찾아야합니다. 당신이 찾아야 할 대수는 펑터를’데이터 유형’l과r가 아닌 캐리어 유형c로 줄이는 함수입니다. 이것은 익숙해 지는데 약간의 시간이 걸리지 만,그것이 카타 모형이 작동하는 방식입니다. 그러나 이것은 당신이 볼 수 있듯이l과r를 무시하게된다는 것을 의미하지는 않습니다.
이전 기사에서와 같이,다음에 기초하여 이형성이 될 함수를 작성하는 것으로 시작한다cata:
eitherF = cata alg . unEitherFix where alg (LeftF l) = undefined alg (RightF r) = undefined
이 컴파일하는 동안,그것의undefined구현,그것은 분명히 유용한 아무것도하지 않습니다. 그러나 나는 그것이 내가 생각하는 데 도움이된다는 것을 안다. LeftF사례에서c유형의 값을 어떻게 반환 할 수 있습니까? 인수를eitherF함수에 전달할 수 있습니다:
eitherF fl = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = undefined
기술적으로c형식의 인수를eitherF에 전달한 다음LeftF사례에서 해당 값을 반환 할 수는 있지만l값을 무시한다는 의미입니다. 이것은 잘못된 것이므로 대신 인수를 함수로 만들고l로 호출하십시오. 마찬가지로RightF사례도 같은 방법으로 처리할 수 있습니다:
eitherF :: (l -> c) -> (r -> c) -> EitherFix l r -> ceitherF fl fr = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = fr r
이 작품. cata에는Functor f => (f a -> a) -> Fix f -> a유형이 있으므로alg에는f a -> a유형이 있음을 의미합니다. EitherF의 경우 컴파일러는alg함수가EitherF l r c -> c형식을 가지고 있음을 유추합니다.
이제 캐리어 유형c가 무엇인지 확인할 수 있습니다. 그것은 대수가 추출하는 유형이며,따라서 이형성이 반환하는 유형입니다.
이 두 가지 모두에 대한 이형성이다. 지금까지 일치 된 바와 같이,그것은 한 쌍의,하지만 지금은 두 가지 기능으로 만든. 당신이 반복적으로 보았 듯이,예를 들어 인수를eitherF으로 쉽게 뒤집을 수 있기 때문에 이것이 유일한 가능한 변형 성은 아닙니다.
하스켈의 내장Data.Either모듈에서either함수와 동형이기 때문에 여기에 표시된 표현을 선택했습니다.이 함수는”Either유형에 대한 사례 분석”함수를 호출합니다. 이 두 가지 함수(eitherF및either)는 위의 방법과 동일합니다.
기준#
eitherF으로 대부분의 다른 유용한 기능을 구현할 수 있습니다. 다음은Bifunctor인스턴스입니다.:
instance Bifunctor EitherFix where bimap f s = eitherF (leftF . f) (rightF . s)
이 인스턴스에서Functor인스턴스는 다음과 같습니다:
instance Functor (EitherFix l) where fmap = second
Functor위에Applicative을 추가할 수 있습니다.:
instance Applicative (EitherFix l) where pure = rightF f <*> x = eitherF leftF (<$> x) f
<*>구현은MaybeFix에 대한<*>구현과 유사합니다. Monad인스턴스의 경우도 마찬가지입니다:
instance Monad (EitherFix l) where x >>= f = eitherF leftF f x
뿐만 아니라EitherFixFoldable,그것은 입니다Bifoldable:
instance Bifoldable EitherFix where bifoldMap = eitherF
흥미롭게도bifoldMap은eitherF과 동일합니다.
Bifoldable인스턴스를 사용하면Foldable인스턴스를 쉽게 구현할 수 있습니다:
instance Foldable (EitherFix l) where foldMap = bifoldMap mempty
bifoldMap(또는eitherF;동일 함)이 인수로 두 함수를 사용하기 때문에mempty의 존재를 찾을 수 있습니다. mempty이 함수입니까?
예,mempty은 함수일 수 있습니다. 여기 있습니다. 여기서m은Monoid인스턴스이고mempty은 해당 모노이드의 신원입니다. 즉,여기에 사용되는 인스턴스입니다.
EitherFix가Bifoldable인 것처럼Bitraversable:
instance Bitraversable EitherFix where bitraverse fl fr = eitherF (fmap leftF . fl) (fmap rightF . fr)
Bitraversable인스턴스를 기반으로Traversable인스턴스를 편안하게 구현할 수 있습니다:
instance Traversable (EitherFix l) where sequenceA = bisequenceA . first pure
마지막으로ana을 이중으로 사용하여 표준Either유형과의 변환을 구현할 수 있습니다cata:
toEither :: EitherFix l r -> Either l rtoEither = eitherF Left Right fromEither :: Either a b -> EitherFix a bfromEither = EitherFix . ana coalg where coalg (Left l) = LeftF l coalg (Right r) = RightF r
이것은EitherFix가Either와 동형임을 보여 주며,다시eitherF과either가 동일하다는 것을 입증합니다.
관계#
이 시리즈에서는 폴드가없는 구조의 이형성,폴드와 일치하는 이형성,그리고 이제 폴드보다 더 일반적인 이형성의 다양한 예를 보았습니다. 이 시리즈에 대한 소개는이 다이어그램을 포함:
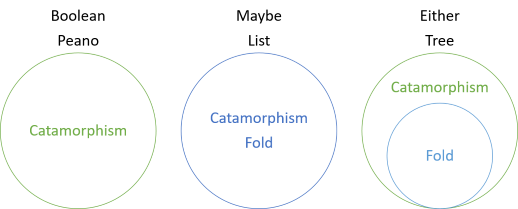
이것은 부울 값과 페아노 숫자가 이형성을 가지고 있지만 폴드가없는 반면 어쩌면 및 목록의 경우 폴드와 이형성은 동일합니다. 그러나 어느 쪽이든 폴드는 이형성의 특별한 경우입니다. 왼쪽이 존재하지 않는’척’중 하나에 대한 폴드. 대신 왼쪽 값은 누락된 오른쪽 값으로 해석됩니다. 따라서 두 값을 모두 접으려면 두 값이 올바른 값이 아닌 경우에 사용할’대체’값을 제공해야 합니다:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e""
위와 같은 세션에서는 동일한 유형의 두 값을 만들 수 있습니다. 오른쪽 케이스는Ordering값이고 왼쪽 케이스는Integer값입니다.
foldr의 경우 왼쪽 케이스에 액세스 할 수있는 방법이 없습니다. 오른쪽Ordering값에 액세스하고 변환할 수 있지만42숫자는 접기 중에 무시됩니다. 대신 기본값""이 반환됩니다.
두 경우 모두에 액세스 할 수있는 이형성과 대조:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"42"
이와 같은 세션에서는 동일한 값을 다시 만들지 만 이형성eitherF을 사용하여 이제 왼쪽 및 오른쪽 사례에 모두 액세스하고 변환 할 수 있습니다. 즉,이형성을 사용하면 접을 수 없는 작업을 수행할 수 있습니다.
그러나 접힘은 이형성의 전문화이지만 이형성은 이형성과 동일하다는 점에 주목하는 것은 흥미롭다.
요약#
둘 중 하나에 대한 이형성은 한 쌍의 함수입니다. 한 함수는 왼쪽 케이스를 변환하고 다른 함수는 오른쪽 케이스를 변환합니다. 어느 값이든 해당 함수 중 하나만 사용됩니다.
원래 이형성의 개념을 접했을 때,나는 이형성과 접힘을 구별하기가 어렵다는 것을 알았다. 내 문제는 내가 실행 한 튜토리얼이 대부분 링크 된 목록을 사용하여 그 경우 폴드가 어떻게 변태성을 보여 주 었는지에 관한 것이 었습니다. 그러나 이것이 항상 그런 것은 아닙니다. ㅏ 이형주의 이다 일반적인 추상화. 반면에 접은 부분은 대부분 컬렉션과 관련이있는 것 같습니다.
이 기사에서는 폴드보다 더 많은 것을 할 수있는 이형성의 첫 번째 예를 보았습니다. 어느 쪽이든,폴드는 이형성의 특별한 경우 일뿐입니다. 그러나 당신은 또한 이형성이 어떻게 이중형과 동일한지 보았습니다. 따라서 이러한 개념이 어떻게 관련되어 있는지 아직 완전히 명확하지 않습니다. 따라서,다음 글에서,당신은 두 배가없는 컨테이너의 예를 얻을 것이다,어디 이형성은,참으로,배의 일반화입니다.
다음:나무 이형성.