오늘은 순환 통계(때로는 방향 통계라고도 함)에 대한 간략한 소개가 될 것입니다. 순환 통계는 단위 원 주위의 벡터로 취한 관찰과 관련된 통계의 흥미로운 세분화입니다. 예를 들어,24 시간 주기로 병원에서 출생 시간을 측정하거나 철새 동물 그룹의 방향 분산을 상상해보십시오. 이 유형의 데이터는 생태학,기후학 및 생화학과 같은 다양한 분야에 관여합니다. 단위 원 주위의 관측치를 측정하는 특성은 가설 검정에 대한 다른 접근 방식을 필요로합니다. 분포는 사용되기 위해 원 주위에”래핑”될 필요가 있으며 샘플 평균 또는 샘플 분산과 같은 기존의 추정기는 물을주지 않습니다.
이 게시물에서 우리는 원형 데이터 세트의 균일 성을 평가하기 위해 라오의 간격 테스트를 수행 할 것입니다. 이것은 기본적인 절차이며 순환 데이터 처리에 대한 소개로 생각해야합니다.
시작하기
우리는 거북이에 대한 가설 테스트를 수행 할 것입니다.이 테스트는 둥지 섬에 10 개의 녹색 바다 거북이의 도착 각도로 구성된 작은 데이터 세트입니다. 우리의 목표는 도착 각도가 방향성의 징후를 표시하거나 임의의 산란을 더 나타내는 위치를 결정하는 것입니다.
먼저circular패키지를 설치하고 거북이 데이터 집합을 연결합니다.
install.packages("circular")require(circular)attach(turtles)
데이터 플로팅
circular패키지에는 자체 플로팅 함수plot.circular가 포함되어 있습니다. 거북이의 도착 각도를 관찰합시다.
plot.circular(arrival)
여기 플롯이 있습니다: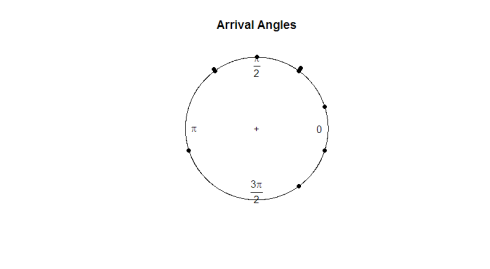
눈 검사를 감안할 때,관찰은 원 주위에 균일 한 것으로 보인다. 데이터가 진정으로 균일한지 확인하기 위해 가설 검정을 실행하려면 각도 데이터와 함께 작동하는 검정 통계량을 개발해야 합니다.
우리가 활용할 수있는 좋은 매개 변수는 무엇입니까? 샘플 평균을 취하는 것은 데이터의 방향에 대해 많이 알려주지 않습니다(180 도는 2 도 및 358 도의 유용한 평균이 아닙니다). 다음 그림에서 표본 평균이 데이터의 모양이나 확산을 나타내는 데 어떻게 사용되지 않는지 관찰하십시오.
mean(arrival)plot.circular(mean(arrival)) 0.9120794
여기 플롯이 있습니다: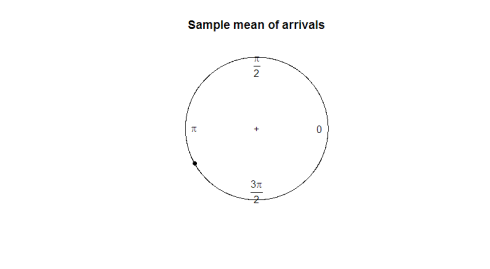
대신 관측치 사이의 평균 공간을 측정하여 방향성을 결정하는 방법을 사용할 것입니다. 이 테스트를 라오의 간격 테스트라고합니다.
라오의 간격 테스트
라오의 간격 테스트는 원형 데이터의 균일 성을 평가하기 위해 개발되었습니다. 관측치 사이의 공간을 사용하여 데이터에 중요한 방향성이 표시되는지 확인합니다. 데이터가 균일하면 관측치의 간격이 균등하게 떨어져 있어야 합니다.
라오의 간격 테스트에 대한 테스트 통계량은 다음과 같습니다.: 이 경우,나는 그(것)들에게 그(것)들에게 그(것)들에게 그(것)들에게 그(것)들에게 그(것)들에게 그(것)들에게 그(것)들에게 그(것)들에게 그(것)들에게 그(것)들에게 그(것)들에게 그(것)들에게 그(것)들에게 그(것)들에게 그(것)들에게 그(것)들에게 그(것)들에게 그(것)들에게 그(것)들에게 그(것)들에게 그(것)들에게 그(것)들에게 그(것)들에게 그(것)들에게 그(것)들에게{1}\)
기본적으로 검정 통계량은 연속된 점 간의 편차를 집계하며,각 점은 데이터 집합의 총 관측치 수로 가중됩니다.
rao.spacing.test()함수를 사용하여 이 가설 테스트를 실행합니다. 우리의 귀무 가설은 데이터가 균일 한 분포 인 반면,대체 상태는 데이터가 방향성의 징후를 보여줍니다. 테스트를 실행하자.
rao.spacing.test(arrival,alpha=.10) Rao's Spacing Test of Uniformity Test Statistic = 127.2689 Level 0.1 critical value = 161.23 Do not reject null hypothesis of uniformity
127 의 시험 통계가 임계 값 161 이하로 떨어지면 데이터는 어떤 방향 으로든 크게 기대지 못합니다. 우리는 거북이 도착이 균일 한 분포라는 가설을 거부 할 수 없습니다.
결론
라오의 간격 테스트는 방향성 추세의 흔적을 보이지 않는 데이터를 결정했다. 우리는 균일성에 대한 귀무 가설을 거부 할 수 없으며 도착 방향과 관련하여 균일 성을 가정 할 것입니다. 이 게시물은 비교적 기본적인 튜토리얼 이었지만 데이터 과학 커뮤니티의 많은 사람들은 이전에 순환 데이터로 작업하지 않았습니다. 그것은뿐만 아니라 여전히 진화하고 통계의 젊은 분야에 다이빙을 할 수있는 흥미로운 하위 주제입니다.
최종 발언
캘리포니아 대학 산타바바라의 라오 잠말라 마다카 박사와 그의 교과서”순환 통계 주제”에 대한 학점을 확대하여 순환 통계 분야에 대한 관심을 불러 일으키고 싶습니다.