Terminologie:
- ID = huidige afvoer van de bron OF de drain-source huidige
- VDS = drain naar source spanning
- L = lengte van het kanaal
Nu voor het ideale geval, in de verzadiging van de regio, ID ‘ s wordt onafhankelijk van VDS d.w.z. in de verzadiging regio kanaal wordt afgeknepen bij de afvoer einde en een verdere toename van de VDS heeft geen effect op het kanaal van de vorm.
maar in de praktijk heeft een toename van het aantal VDS invloed op het kanaal. In het verzadigingsgebied, wanneer VDS toeneemt, wordt het kanaalknelpunt iets van de afvoer naar de bron verplaatst, terwijl het afvoerelektronenveld het terugduwt. Het gebied van de omgekeerde biasuitputting verbreedt en de efficiënte kanaallengte vermindert met een hoeveelheid ∆L voor een verhoging van VDS.
het kanaal “raakt” de afvoer niet meer aan en krijgt een asymmetrische vorm die dunner is aan het uiteinde van de afvoer. Dit fenomeen staat bekend als kanaallengte modulatie.
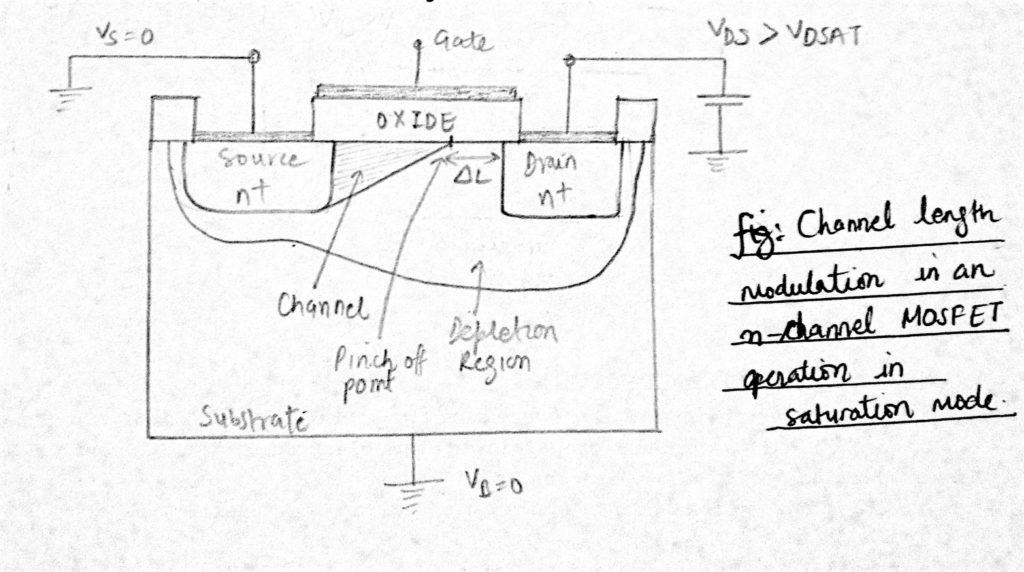
bij grote hulpmiddelen is dit effect verwaarloosbaar, maar bij kortere hulpmiddelen is ∆L/L belangrijk. Ook in het verzadigingsgebied als gevolg van modulatie van de kanaallengte neemt IDS toe met de toename van VDS en neemt ook toe met de afname van de kanaallengte L.
de spanningsstroomcurve is in dit gebied niet meer vlak.
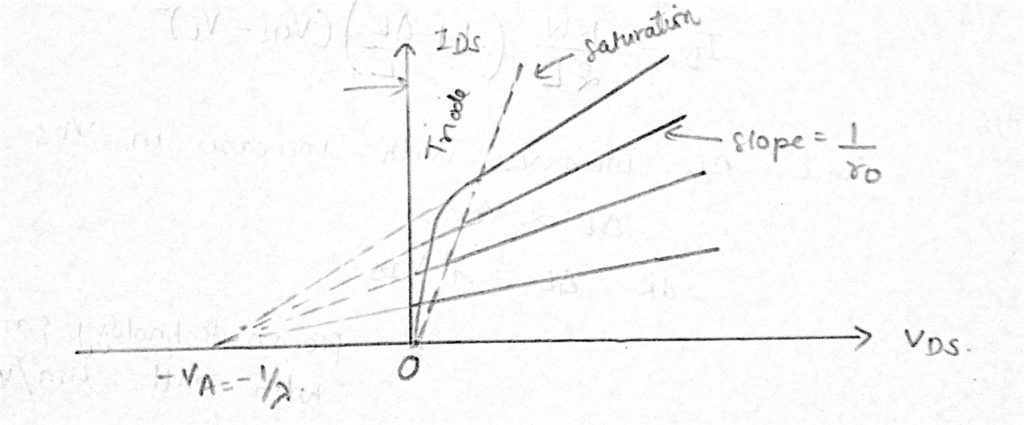
de afvoerstroom met kanaallengte modulatie wordt gegeven door:
afleiding:
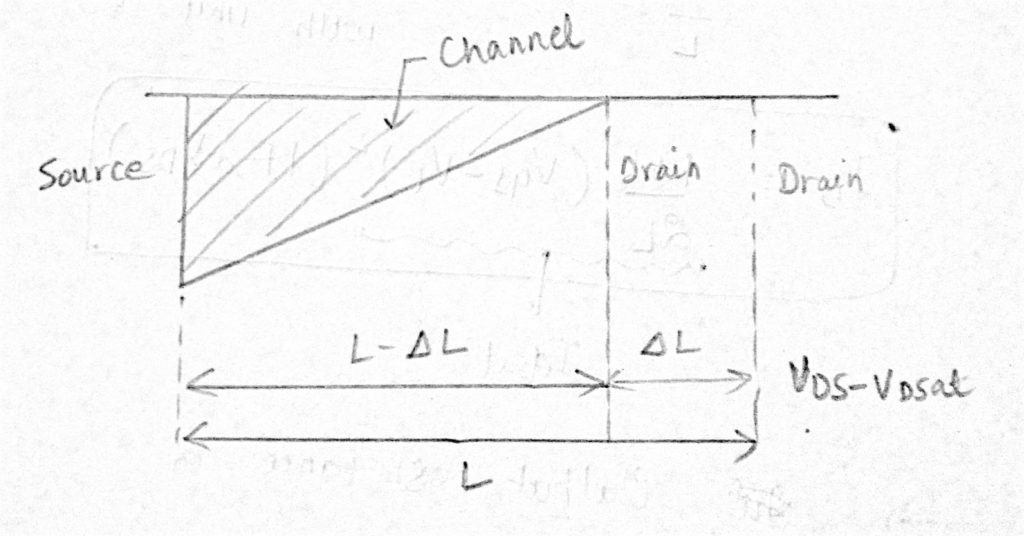
om rekening te houden met de afhankelijkheid van ID op VDS in het verzadigingsgebied, vervang L door L – ∆L. we weten dat in het verzadigingsgebied, afvoer naar bronstroom (IDS = ID) wordt gegeven door:
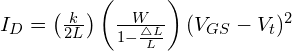
in de Veronderstelling 
Sinds ∆L toeneemt met de toename van VDS
OF
waar, 
= proces technologie parameter eenheid µm/V.
daarom,
waar,
= proces technologie parameter eenheid V-1
