MHOF解析のためのFDTDおよびFDMアルゴリズム
光学光は本質的に電磁波であり、したがってその伝搬特性は、マクスウェル方程式として総称される電気力学の法則によって支配される。 フォトニックバンドギャップ構造を持つMHOFにおける光信号の誘導は,同一の空気孔の周期的配置による建設的干渉効果に依存することが知られている。 一方、空気孔の大きさ、位置、またはその両方がランダムになると、全内部反射の現象が起こり、コアとクラッドの間の指数差が光閉じ込めを提供し、そ 任意のMhofsのような複雑な構造の伝搬特性は解析的な方法では容易に計算できないが,電磁問題を数値的に解く方法がある。
このセクションでは、任意の空気孔分布を持つホーリー光ファイバの解析への拡張を考慮して、有限差分時間領域(FDTD)と有限差分法(FDM)の二つの数値技術に対 これらの技術のそれぞれには一定の利点があります。 FDTD法を用いて,有限体積の空間内の連続電磁場を空間格子内の異なる点と等間隔のサンプリング点でサンプリングした。 点でサンプリングしたデータを,与えられた導波路におけるスプリアスモード解を生成することなく,許容モードの数値計算に使用した。 誘導モードの伝搬定数の計算には有効な手法であるにもかかわらず,FDTD法は個々のモード場分布の評価には適していない。 これは、ソースが無限スペクトルをカバーする時間領域のインパルス関数であるため、場分布解はすべての可能なモードの重ね合わせであるためです。 FDTDから利用可能な伝搬定数によるこの問題を軽減するために,個々のモードフィールド分布をfdmを用いて得た。
この方法はマクスウェル方程式に基づく堅牢な解を提供し、複素値の材料特性に容易に対応できるため、FDTDは近年かなりの人気を得ています。 任意の材料物体は、電界成分位置が所望の誘電率および透磁率の値で配置される単位セルを構築することによって近似することができる。 オブジェクトのジオメトリが数値シミュレーション領域で指定されると、ソース条件が領域のどこかでモデル化されます。 最初は、計算ドメイン内のすべてのフィールドが同じようにゼロであると仮定されます。 そして,入射波を強制して数値計算領域に入る。
MKS単位系を用いて、まず次のように表されるマクスウェルのカール方程式を考えてみましょう:
ここで、λはf/mの電気誘電率定数、λはH/mの透磁率定数である。 なお、電界成分と磁界成分(E X、Ey、Ez、H X、H Y、H Z)は相互に関連している。 つまり、マクスウェルの方程式は電場と磁場の値を直接生成するのではなく、むしろ電場と磁場の値の間の変化率を関連づけます。
二次精度の空間-時間微分に対する中心差分近似を採用することにより、三次元(3D)FDTD定式化における代表例として、以下の近似を開発することがで:<3 6 8 4><9 4 8 1>Exn+1(i+1 2,j,k)=Exn(i+1 2,j,k)+Δ T Θ0Θ R(i+1 2,j,k){−}E4<8 8 7 0><9 4 8 1>Hyn+1 2(i+1 2,j,k+1 2)=Hyn−1 2(i+1 2,j,k+1 2)+Δ T Θ{−}E5<8 8 7 0><9 4 8 1><9 4 8 2><9 4 8 3><9 4 8 4><9 4 8 5><9 4 8 6><9 4 8 7><9 4 8 8><9 4 8 8><9 4 8 9><9 4 9 9><9 4 9 9><9 4 9 9><9 4 9 9><9 4 9 9><9 4 9 9><9 4 9 9><9 4 9 9><9 4 9 9><9 4 9 9><9 4 9 9><9 4 8 1>hzn+1 2(I+1 2,j+1 2,k)=Hzn−1 2(i+1 2,j+1 2,K)+Δ t≦{−}E6<8 8 7 0><2 8 1 6>ただし、i,J,K,Nは、それぞれΔ x,Δ y,Δ z,Δ tの整数である。
MHOFsなどの光ファイバは、一般的に伝搬方向に沿った変動がなく、材料特性の変動は図3に示すように横方向に限定されるため、3D FDTD定式化をコンパクトな二次元(2D)FDTDアルゴリズムに単純化することができる。 軸伝搬定数(β)を持つフェーザ表記法を使用することにより、場のz依存性はexp(-j θ z)であるため、zに関する一次偏導関数は-j θに置き換えられます。 離散化された空間領域における一次導関数に必要な二つの隣接する場は,それらの間の中間点における場によって表すことができる。 これら二つの事実に基づいて、例として以下の定式化が得られる:
得られた2Dアルゴリズムは、必要なコンピュータメモリ割り当てと実行時間の大幅な削減を利用する。 したがって,波伝搬方向に沿って均一な任意の導波路のコンピュータ計算のためには,導波路の断面のモデリングだけで十分である。
この効率的なアルゴリズムに加えて、任意の電磁物体に対する2次元空間における無限媒体は、高度な現在の技術であっても計算領域にコンピュー 無限大まで伸びる領域をモデル化するために,計算領域の外側格子境界において,非常に効果的な吸収境界条件(ABC)として完全整合層(PML)を設計した。 理想的には、吸収媒体は少数の格子細胞だけ厚く、非常に吸収し、すべての衝突の波にreflectionless、作動の波長のフルレンジに有効である。
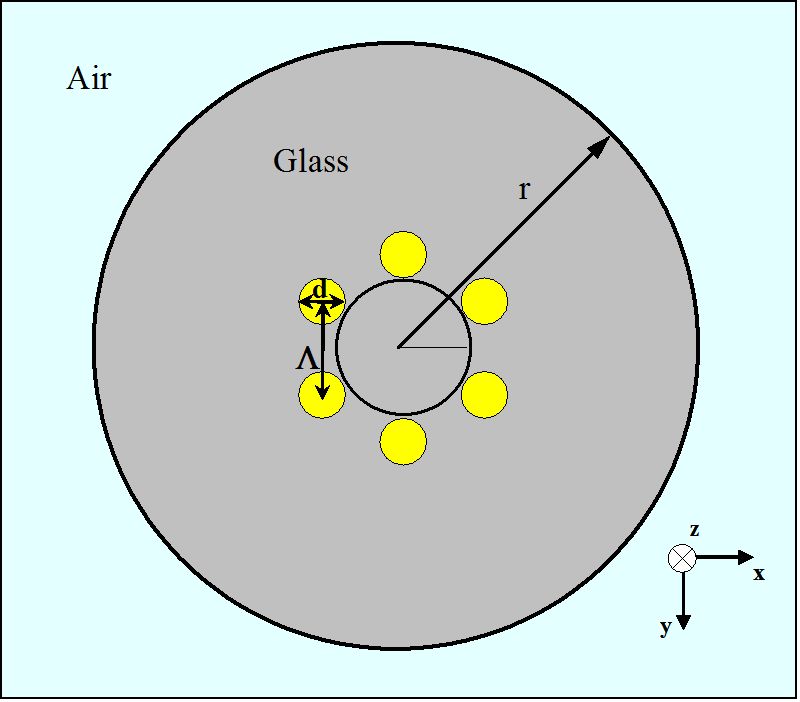
図3.
六方晶配置の空気孔の一層を有するMHOFの断面図
FDTDアルゴリズムの開発と同様に,fdm定式化は結合Maxwell方程式から導くことができる。 線形および等方性媒質における連続波の場合、Eqs(2)と(3)を組み合わせると、次のベクトル波動方程式が得られます:
ここで、nは屈折率、k0は自由空間における伝搬定数です。 光ファイバのような多くの導波路デバイスは、z不変構造、または区分的z不変構造と見なすことができます。 これらの構造では、屈折率n(x,y,z)は伝搬方向zに沿ってゆっくりと変化し、これはほとんどのフォトニック導波デバイスに有効です。 のベクトル恒等式を用いて∇×∇×=∇(∇⋅)−∇2, Eq(8)は
と書くことができます。z軸に沿った無視できる時間依存性を合理的に仮定すると、eq(9)のようなfdm定式化は、空間導関数を有限差分近似に置き換えることによって実装することができます。 ここでは、この横方向成(9)
に、下付き文字”t”は横方向成。 縦方向成分は、以下のゼロ発散(ガウスの法則)制約を適用することによって容易に得ることができるので:
横方向の成分は、光導波路における電磁場の全ベクトル特性を記述するのに十分である。
MHOFsの誘導特性の初期調査のために、図3に示す光ファイバをコンピュータ解析します。 一般に、MHOF形状は、図3に示すように、ピッチ長(Λ)と直径(d)の2つのパラメータで記述することができます。 ここで、ピッチ長は、円筒形状の二つの最も近い空気孔の中心間の距離である。 図3のMHOFでは、それぞれの小さな空気孔の直径は1.4μ mであり、Λ=1.7μ mの六角形を構成しています。 黄色領域の六つの空気孔を囲むガラス部分は、1.45の屈折率を有する。 ホーリー繊維の外側半径(r)は1 0μ mと仮定する。 また、MHOFの外側領域は空気である。
ホーリーファイバの断面が適切な計算領域で定義されると、Fdtdシミュレーションは、ガウス源を定義するときのσ、安定したシミュレーションのためのΔ T、時間領域のデータをサンプリングするためのタイムステップの合計数(ntot)、βの妥当な値など、いくつかの指定されたパラメータで行うことができる。 ここで、数値発散を回避し、FDTDアルゴリズムの安定性を確保するためには、以下の安定性条件を満たすように適切なΔ Tを選択する必要があります:
ここで、cMは与えられた数値モデル内の最大波位相速度です。 FDTD解析の背後にあるメカニズムを要約すると、コンピュータシミュレーションは次の手順で進行します:
-
適切なパラメータ値(λ、Δ T、ntot、およびβ)を選択します)
-
時間領域におけるフィールドコンポーネントのデータサンプリング
-
時間データのフーリエ変換を取る
-
フィールド成分のスペクトルデータを取得する
-
β値に関連付けられたピックモード周波数
-
βおよびモード周波数データの収集
-
モードインデックスと波長のプロットを作成します
図4は、FDTDから得られた特性曲線を示しています 図3で定義されたMHOFの最初の三つの低次モードの計算。
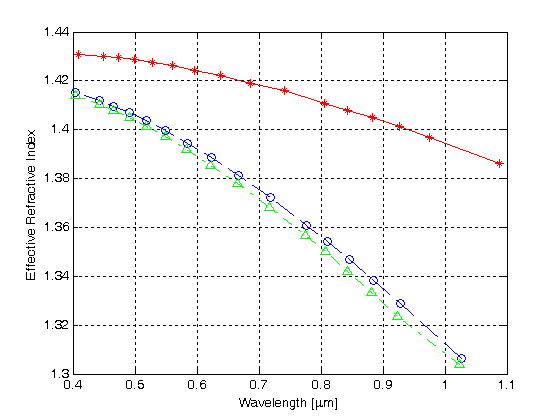
図4.
空気孔の一つの層を持つMHOFにおける最初の三つのモードの有効屈折率対波長
星のシンボルを持つ赤の曲線は、第一のモードと波長に対する正規化された伝播定数をプロットし、青と緑の曲線は、それぞれ第二のモードと第三のモードの正規化された伝播定数を示しています。 その結果,単一の六方晶空気孔クラッド層を有するHMOFはマルチモードガイディングを支持することが分かった。