veronderstelde kennis
studenten zullen in eerdere jaren uitgebreide informele ervaring met meetkunde hebben gehad, en dit zal een goede intuïtieve basis bieden voor de meer systematische benadering van meetkunde die geschikt is in de jaren 7-10. De specifieke onderwerpen uit de jaren F-6 die relevant zijn voor deze module zijn::
- het gebruik van kompassen en linialen en het zorgvuldig tekenen van geometrische figuren.
- soorten hoeken, waaronder ten minste rechte hoeken, scherpe hoeken, stompe hoeken en
reflexhoeken. - driehoeken, met inbegrip van een informele inleiding tot gelijkbenige en gelijkzijdige driehoeken.
- Quadrilateralen, met inbegrip van een informele inleiding op vierkanten, rechthoeken, parallelogrammen, trapezia en ruiten.
- informele ervaring met vertalingen, reflecties, rotaties en vergrotingen,
en met symmetrie in de context van activiteiten zoals het vouwen van een gelijkbenige driehoek, rechthoek of ruit.
Motivatie
 geometrie wordt gebruikt om de wereld om ons heen te modelleren. Een blik op de daken van huizen onthult driehoeken, trapezia en rechthoeken, terwijl tegelpatronen in trottoirs en badkamers gebruik maken van zeshoeken, vijfhoeken, driehoeken en vierkanten. Bouwers, tegelzetters, architecten, grafisch ontwerpers en webontwerpers gebruiken routinematig geometrische ideeën in hun werk. Het classificeren van dergelijke geometrische objecten en het bestuderen van hun eigenschappen zijn erg belangrijk. Geometrie heeft ook veel toepassingen in de kunst.
geometrie wordt gebruikt om de wereld om ons heen te modelleren. Een blik op de daken van huizen onthult driehoeken, trapezia en rechthoeken, terwijl tegelpatronen in trottoirs en badkamers gebruik maken van zeshoeken, vijfhoeken, driehoeken en vierkanten. Bouwers, tegelzetters, architecten, grafisch ontwerpers en webontwerpers gebruiken routinematig geometrische ideeën in hun werk. Het classificeren van dergelijke geometrische objecten en het bestuderen van hun eigenschappen zijn erg belangrijk. Geometrie heeft ook veel toepassingen in de kunst.
net zoals rekenkunde getallen als basisobjecten heeft, zijn punten, lijnen en Cirkels de basisbouwstenen van de vlakke meetkunde.
In de meetkunde van de middelbare school beginnen we met een aantal intuïtieve ideeën (punten, lijnen en hoeken) die in het geheel niet gemakkelijk te definiëren zijn, gevolgd door een aantal definities (verticaal tegengestelde hoeken, parallelle lijnen, enzovoort) en daaruit leiden we belangrijke feiten af, die vaak stellingen worden genoemd. Op de middelbare school moet de strengheid van het ene jaar op het andere langzaam toenemen, maar in elke fase is een duidelijke omschrijving zeer belangrijk en moet worden benadrukt. De meetkunde biedt studenten dus de mogelijkheid om hun geometrische intuïtie te ontwikkelen, die op veel gebieden van het leven toepasbaar is, en ook om te leren hoe logische argumenten te construeren en deducties te maken in een omgeving die voor het grootste deel onafhankelijk is van het aantal.
inhoud
punten en lijnen
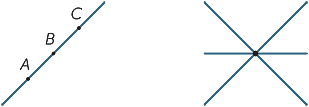
de eenvoudigste objecten in de vlakke geometrie zijn punten en lijnen. Omdat ze zo eenvoudig zijn, is het moeilijk om precieze definities van hen te geven, dus in plaats daarvan proberen we studenten een ruwe Beschrijving van hun eigenschappen te geven die in lijn zijn met onze intuïtie. Een punt markeert een positie, maar heeft geen grootte. In de praktijk, wanneer we een punt tekenen heeft het duidelijk een bepaalde breedte, maar het vertegenwoordigt een punt in onze verbeelding. Een lijn heeft geen breedte en strekt zich oneindig uit in beide richtingen. Wanneer we een lijn tekenen heeft het breedte en heeft het uiteinden, dus het is niet echt een lijn, maar vertegenwoordigt een lijn in onze verbeelding. Gegeven twee verschillende punten A en B is er één (en slechts één) lijn die door beide punten gaat. We gebruiken hoofdletters om naar punten te verwijzen en regels te noemen door twee punten op de regel te vermelden, of door kleine letters te gebruiken zoals  en m. de gegeven regel hieronder wordt dus aangeduid als de regel AB of als de regel
en m. de gegeven regel hieronder wordt dus aangeduid als de regel AB of als de regel  .
.

gegeven twee verschillende lijnen, zijn er twee mogelijkheden: ze kunnen ofwel op één punt samenkomen of ze kunnen nooit samenkomen, ongeacht hoe ver ze worden uitgebreid (of geproduceerd). Lijnen die elkaar nooit ontmoeten worden parallel genoemd. In het tweede diagram schrijven we AB ||CD.
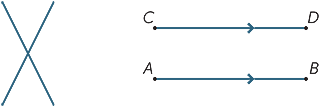
drie (of meer) punten die op een rechte lijn liggen worden collineair genoemd.
drie (of meer) regels die op één punt samenkomen worden gelijktijdig genoemd.
|
|
|
| collineair |
gelijktijdig |
Oefening 1
Trek drie lijnen die niet gelijktijdig zijn, zodat er geen twee evenwijdig zijn.
Oefening 2
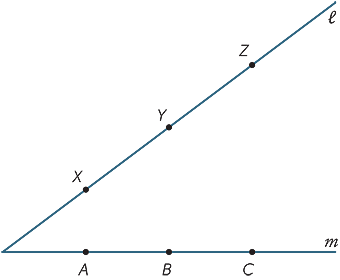
Maak een grote kopie van het onderstaande diagram. De punten X, Y, Z zijn alle punten op de lijn  en A, B, C zijn alle punten op de lijn m. Join AY en XB noemen hun snijpunt R. Join BZ en YC en noemen hun snijpunt P. Join CX en ZA en noemen hun snijpunt Q. Wat valt je op aan de punten P, Q, R? (Dit resultaat wordt Pappus’ stelling genoemd, C. 340 AD.)
en A, B, C zijn alle punten op de lijn m. Join AY en XB noemen hun snijpunt R. Join BZ en YC en noemen hun snijpunt P. Join CX en ZA en noemen hun snijpunt Q. Wat valt je op aan de punten P, Q, R? (Dit resultaat wordt Pappus’ stelling genoemd, C. 340 AD.)
intervallen, stralen en hoeken
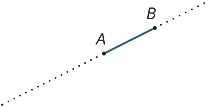 stel dat A en B twee punten op een lijn zijn. Het interval
stel dat A en B twee punten op een lijn zijn. Het interval
AB is het deel van de lijn tussen A en B, inclusief de twee eindpunten.
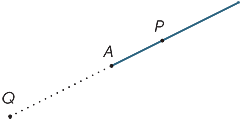 het punt A in het diagram verdeelt de lijn in twee stukken die stralen worden genoemd. De straal AP is die straal die het punt P (en het punt A) bevat.
het punt A in het diagram verdeelt de lijn in twee stukken die stralen worden genoemd. De straal AP is die straal die het punt P (en het punt A) bevat.
Hoeken
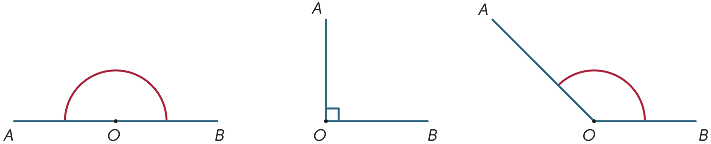
 in het diagram wordt het gearceerde gebied tussen de stralen OA en OB de hoek AOB of de hoek BOA genoemd. Het hoekteken
in het diagram wordt het gearceerde gebied tussen de stralen OA en OB de hoek AOB of de hoek BOA genoemd. Het hoekteken ![]() is geschreven dus schrijven we
is geschreven dus schrijven we ![]() AOB.
AOB.
 het gearceerde gebied buiten wordt de reflexhoek genoemd die wordt gevormd door OA en OB. Meestal, tenzij we het woord reflex specificeren, verwijzen al onze hoeken naar het gebied tussen de stralen en niet daarbuiten.
het gearceerde gebied buiten wordt de reflexhoek genoemd die wordt gevormd door OA en OB. Meestal, tenzij we het woord reflex specificeren, verwijzen al onze hoeken naar het gebied tussen de stralen en niet daarbuiten.
de grootte van een hoek
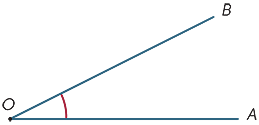 stel je voor dat de straal OB rond het punt O wordt gedraaid totdat hij langs OA ligt. De hoeveelheid draaien wordt de grootte van de hoek AOB genoemd. We kunnen ook de grootte van de reflexhoek definiëren.
stel je voor dat de straal OB rond het punt O wordt gedraaid totdat hij langs OA ligt. De hoeveelheid draaien wordt de grootte van de hoek AOB genoemd. We kunnen ook de grootte van de reflexhoek definiëren.
we zullen vaak kleine Griekse letters, α, β, γ, gebruiken … om de grootte van een hoek weer te geven.
de grootte van de hoek die overeenkomt met een volledige omwenteling werd gedeeld (door de Babyloniërs) in 360 gelijke delen, die we graden noemen. (Ze kozen waarschijnlijk 360 omdat het dicht bij het aantal dagen in een jaar was.) Dus de grootte van een rechte hoek is 180° en de grootte van een rechte hoek is 90°. Andere hoeken kunnen (ongeveer) worden gemeten met behulp van een gradenboog.
|
|
||
| rechte hoek | rechte hoek |
stompe hoek |
hoeken worden ingedeeld op basis van hun grootte. We zeggen dat een hoek met grootte α acuut
is (een woord dat ‘scherp’ betekent) als 0° < α < 90°, α stomp (een woord dat ‘bot’ betekent) als
90° < α < 180° en α reflex is als 180° < α < 360°.
aangezien de gradenboog twee schalen heeft, moeten leerlingen voorzichtig zijn bij het tekenen en
bij het meten van hoeken. Het is de moeite waard om een gradenboog te gebruiken om een aantal hoeken te tekenen, zoals 30°, 78°, 130°, 163°.
Oefening 3
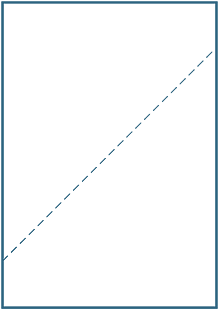 vouw een A4-vel papier dat overeenkomt met de (diagonaal) tegenovergestelde hoeken. Teken een lijn langs de vouw die wordt gevormd en meet de hoeken tussen de vouw en de zijkant.
vouw een A4-vel papier dat overeenkomt met de (diagonaal) tegenovergestelde hoeken. Teken een lijn langs de vouw die wordt gevormd en meet de hoeken tussen de vouw en de zijkant.
in de bovenstaande oefening vormen de twee hoeken samen een rechte lijn en komen zo bij 180°. Twee hoeken die 180° toevoegen worden aanvullende hoeken genoemd; zo zijn 45° en 135° aanvullende hoeken.
twee hoeken die 90° optellen worden complementair genoemd; dus 23° en 67° zijn
complementaire hoeken.
hoeken op een punt
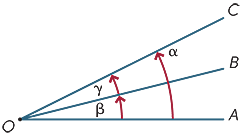 twee hoeken op een punt zouden naast elkaar liggen als ze een gemeenschappelijke straal delen. Daarom staan in het diagram
twee hoeken op een punt zouden naast elkaar liggen als ze een gemeenschappelijke straal delen. Daarom staan in het diagram ![]() AOB en
AOB en ![]() BOC naast elkaar.
BOC naast elkaar.
aangrenzende hoeken kunnen worden toegevoegd, dus in het diagram
α = β + γ.
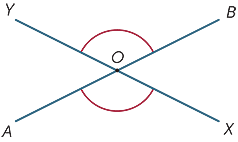
wanneer twee lijnen elkaar snijden, worden op het snijpunt vier hoeken gevormd.
in het diagram worden de hoeken met ![]() AOX en
AOX en ![]() BOY verticaal tegenovergesteld genoemd.
BOY verticaal tegenovergesteld genoemd.
 sinds
sinds
-
 AOX is het supplement van
AOX is het supplement van  doos (rechte hoek).
doos (rechte hoek). -
 BOY is ook het supplement van
BOY is ook het supplement van  BOX (rechte hoek),
BOX (rechte hoek),
we kunnen concluderen dat deze verticaal tegengestelde hoeken, ![]() AOX en
AOX en ![]() BOY gelijk zijn. We hebben dus onze eerste
BOY gelijk zijn. We hebben dus onze eerste
belangrijke geometrische stelling:
verticaal tegengestelde hoeken zijn gelijk.
een resultaat in de meetkunde (en in de wiskunde in het algemeen) wordt vaak een stelling genoemd. Een stelling is een belangrijke stelling die kan worden bewezen door logische deductie. Het bovenstaande argument is een bewijs van de stelling; soms worden bewijzen formeel gepresenteerd na de stelling.
 als twee lijnen elkaar snijden zodat alle vier de hoeken loodrecht zijn,dan zijn de lijnen loodrecht.
als twee lijnen elkaar snijden zodat alle vier de hoeken loodrecht zijn,dan zijn de lijnen loodrecht.
hoeken op een punt-Geometrische argumenten
de volgende redenen kunnen worden gebruikt in geometrische argumenten:
- aangrenzende hoeken kunnen worden toegevoegd of afgetrokken.
- hoeken in een omwenteling toevoegen aan 360°.
- hoeken in een rechte lijn optellen tot 180°.
- verticaal tegengestelde hoeken zijn gelijk.
transversale en parallelle lijnen
 een transversale lijn is een lijn die twee andere lijnen ontmoet.
een transversale lijn is een lijn die twee andere lijnen ontmoet.
overeenkomstige hoeken
transversale hoeken vormen verschillende hoeken. In de onderstaande diagrammen worden de twee gemarkeerde hoeken overeenkomstige hoeken genoemd.
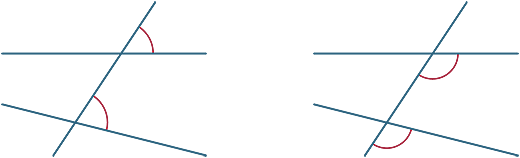
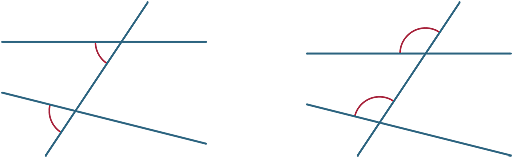
 we bekijken nu wat er gebeurt als de twee door de transversale lijnen parallel lopen.
we bekijken nu wat er gebeurt als de twee door de transversale lijnen parallel lopen.
als de hoek α groter was Dan β dan zou CD AB links van F kruisen en als deze kleiner was Dan β, zou het rechts van F kruisen. aangezien de lijnen dus helemaal niet kruisen, kan α niet kleiner of groter zijn dan β en dus gelijk zijn aan β.
stel je voor dat je de hoek QGD vertaalt langs GF totdat G samenvalt met F. aangezien de lijnen parallel zijn, zouden we verwachten dat de hoek α samenvalt met de hoek β. Deze observatie leidt ons tot het vermoeden dat:
de overeenkomstige hoeken gevormd uit parallelle lijnen zijn gelijk.
we kunnen dit resultaat niet bewijzen, hoewel we hebben aangetoond dat het meetkundig plausibel is. We zullen het accepteren als een axioma van de meetkunde. Een axioma is een stelling die we niet kunnen bewijzen, maar die intuïtief redelijk is. Merk op dat veel van de feiten die we al hebben vermeld, zoals: aangrenzende hoeken kunnen worden toegevoegd, en twee punten bepalen een lijn etc., zijn ook axioma ‘ s, hoewel we ze niet expliciet op deze manier hebben gesteld.
alternatieve hoeken
in elk diagram worden de twee gemarkeerde hoeken alternatieve hoeken genoemd (omdat ze aan alternatieve zijden van de transversale).

 als de lijnen AB en CD parallel zijn, dan zijn de alternatieve hoeken gelijk. Dit resultaat kan nu worden bewezen.
als de lijnen AB en CD parallel zijn, dan zijn de alternatieve hoeken gelijk. Dit resultaat kan nu worden bewezen.
![]() DGQ = α (overeenkomstige hoeken, AB / / CD)
DGQ = α (overeenkomstige hoeken, AB / / CD)
![]() DGQ = β (verticaal tegenover elkaar liggende hoeken bij G)
DGQ = β (verticaal tegenover elkaar liggende hoeken bij G)
dus α = β.
samenvattend:
alternatieve hoeken gevormd uit parallelle lijnen zijn gelijk.
Co-interieur hoeken
ten slotte worden in elk diagram hieronder de twee gemarkeerde hoeken genoemd co-interieur hoeken en liggen aan dezelfde zijde van de transversale.

als de lijnen AB en CD evenwijdig zijn, dan is het duidelijk dat de co-interieur hoeken niet gelijk zijn, maar het blijkt dat ze aanvullend zijn, dat wil zeggen dat de som 180° is .
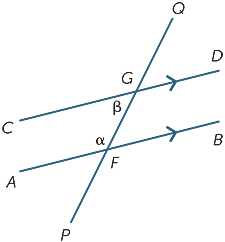 dit is een resultaat dat ook gemakkelijk te bewijzen is:
dit is een resultaat dat ook gemakkelijk te bewijzen is:
![]() BFG = β (alternatieve hoeken, AB ||CD)
BFG = β (alternatieve hoeken, AB ||CD)
α + β = 180° (rechte hoek op F)
samenvattend:
Co-interieur hoeken gevormd uit parallelle lijnen zijn aanvullend.
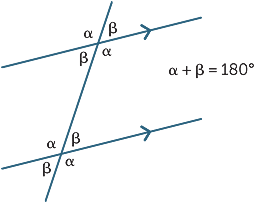 de drie resultaten kunnen worden samengevat
de drie resultaten kunnen worden samengevat
door het volgende diagram:
numerieke voorbeelden
gegeven informatie over de hoeken in een diagram, kunnen we de bovenstaande resultaten gebruiken om de grootte van andere hoeken in het diagram te vinden. Dit is een eenvoudige maar zeer belangrijke vaardigheid, vaak informeel aangeduid als angle chasing. Bij het oplossen van problemen is de volgorde van de stappen niet altijd uniek. Er kunnen verschillende, maar even geldige benaderingen zijn.
bijvoorbeeld, in het volgende diagram, zoeken we de grootte van hoek BAC.

![]() DCA = 102° (alternatieve hoeken, AC|BD)
DCA = 102° (alternatieve hoeken, AC|BD)
![]() BAC = 78° (co-interieur hoeken, AB / / CD)
BAC = 78° (co-interieur hoeken, AB / / CD)
Oefening 4
gebruik een alternatieve reeks stappen om ![]() BAC te vinden.
BAC te vinden.
Oefening 5
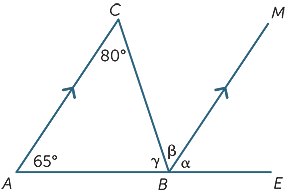 gebruik alleen eigenschappen van parallelle lijnen en zoek (met redenen) de ontbrekende hoeken in het volgende diagram.
gebruik alleen eigenschappen van parallelle lijnen en zoek (met redenen) de ontbrekende hoeken in het volgende diagram.
oefening 6
Zoek de waarde van α in het volgende diagram.
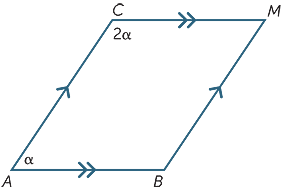
Converse statements
veel stellingen in de wiskunde hebben een converse, waarbij de implicatie in de tegenovergestelde richting gaat. Bijvoorbeeld, het statement
‘ elk even getal eindigt op 0, 2, 4, 6 of 8.’
heeft converse
‘ elk getal dat eindigt op 0, 2, 4, 6 of 8 is even.”
deze stelling en het omgekeerde zijn beide waar, maar dit is lang niet altijd
het geval.
bijvoorbeeld, de volgende twee statements zijn conversaties van elkaar:
‘ elk veelvoud van 4 is een even getal.’
‘ elk even getal is een veelvoud van 4.’
en hier is het eerste statement waar, maar het tweede is onwaar.
oefening 7
afschrijving:
a![]() een waar geometrisch statement waarvan het omgekeerde ook Waar is,
een waar geometrisch statement waarvan het omgekeerde ook Waar is,
b![]() onwaar geometrisch statement waarvan het omgekeerde ook Waar is,
onwaar geometrisch statement waarvan het omgekeerde ook Waar is,
c![]() een onwaar geometrisch statement waarvan het omgekeerde ook onwaar is.
een onwaar geometrisch statement waarvan het omgekeerde ook onwaar is.
de omgekeerde stellingen voor parallelle lijnen
we hebben gezien dat overeenkomstige hoeken gevormd uit parallelle lijnen gelijk zijn. We kunnen het omgekeerde statement als volgt opschrijven.
Statement: als de lijnen evenwijdig zijn, dan zijn de overeenkomstige hoeken gelijk.
Converse: Als de corresponderende hoeken gelijk zijn, dan zijn de lijnen evenwijdig.
het omgekeerde statement is ook waar en wordt vaak gebruikt om te bewijzen dat twee lijnen parallel zijn. Hetzelfde geldt voor alternatieve en co-interieur hoeken.
Statement: als de lijnen evenwijdig zijn, dan zijn de alternatieve hoeken gelijk.
Converse: als de alternatieve hoeken gelijk zijn, dan zijn de lijnen parallel.
Statement: als de lijnen evenwijdig zijn, dan zijn de co-interieur hoeken aanvullend.
Converse: Als de co-interieur hoeken zijn aanvullend, dan zijn de lijnen parallel.
in elk diagram zijn de regels AB en CD dus parallel.

oefening 8
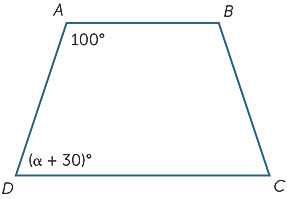 welke waarde van α maakt AB parallel aan CD?
welke waarde van α maakt AB parallel aan CD?
proefdrukken van de drie conversaties
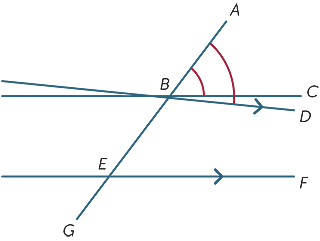 we veronderstellen dat de overeenkomstige hoeken gevormd door de transversale gelijk zijn en we laten zien dat de lijnen parallel zijn.
we veronderstellen dat de overeenkomstige hoeken gevormd door de transversale gelijk zijn en we laten zien dat de lijnen parallel zijn.
in het diagram veronderstellen we dat ![]() ABC =
ABC = ![]() BEF.
BEF.
als BC en EF niet parallel zijn, teken dan
BD parallel aan EF.
nu omdat BD en EF parallel zijn ![]() ABD =
ABD = ![]() BEF en dus
BEF en dus ![]() ABC =
ABC = ![]() ABD wat duidelijk onmogelijk is tenzij de regels BC en BD hetzelfde zijn. Vandaar dat de lijnen BC en EF parallel zijn.
ABD wat duidelijk onmogelijk is tenzij de regels BC en BD hetzelfde zijn. Vandaar dat de lijnen BC en EF parallel zijn.
de andere bewijzen volgen op dezelfde wijze.
oefening 9
Geef een bewijs van de tweede omgekeerde stelling (alternatieve hoeken).
hoek som van een driehoek
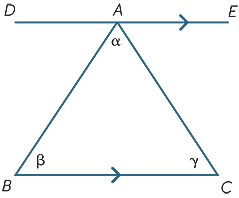 de resultaten uit de vorige paragraaf kunnen worden gebruikt om een van de belangrijkste feiten in de meetkunde af te leiden − de hoeksom van een driehoek is 180° .
de resultaten uit de vorige paragraaf kunnen worden gebruikt om een van de belangrijkste feiten in de meetkunde af te leiden − de hoeksom van een driehoek is 180° .
we beginnen met driehoek ABC met hoeken α, β, γ zoals getoond. Teken de lijn dae parallel aan BC. Daarna,
![]() DAB = β (alternatieve hoeken, BC / / DE)
DAB = β (alternatieve hoeken, BC / / DE)
![]() EAC = γ (alternatieve hoeken, BC / / DE)
EAC = γ (alternatieve hoeken, BC / / DE)
α+ β + γ = 180° (rechte hoek).
zo hebben we bewezen dat de stelling
de som van de hoeken in een driehoek 180°is.
een vierhoek is een vlakgetal begrensd door vier zijden.
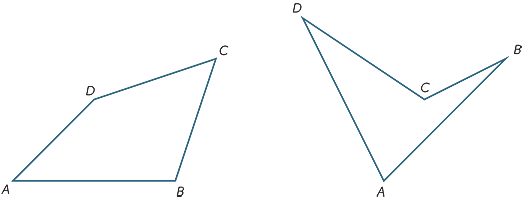
oefening 10
door de vierhoek ABCD te delen in twee driehoeken, vindt u de som van de hoeken.
het materiaal in deze module is begonnen met het plaatsen van meetkunde op een redelijk systematische basis van zorgvuldig gedefinieerde objecten, axioma ‘ s die moeten worden aangenomen, en stellingen die we hebben bewezen. Op deze basis kunnen we een systematisch overzicht van de vlakke meetkunde ontwikkelen waarbij:
- stelling van Pythagoras
- congruentie en congruente driehoeken
- gelijkenis en soortgelijke driehoeken
- gelijkbenige en gelijkzijdige driehoeken
- speciale vierhoeken, waaronder vierkanten, rechthoeken, parallelogrammen, ruiten en trapezia
- de meetkunde van cirkels.
vlakke meetkunde zal ook fundamenteel zijn in vele andere gebieden van de jaren 7-10 wiskunde:
- transformaties
- driedimensionale geometrie
- gebieden en volumes
- trigonometrie
- coördinaatgeometrie
- de grafieken van cirkels en parabolen.
de ideeën van raaklijnen en gebieden leiden op hun beurt tot calculus in de jaren 11-12.
geschiedenis en toepassing
geschiedenis
de ongelooflijke bouwwerken van de piramides en de enorme tempels van Egypte tonen aan dat de Egyptenaren een zeer goede praktische kennis en begrip van de basismeetkunde moeten hebben gehad, op zijn minst op praktisch niveau. Aan de andere kant is er geen bewijs dat ze die kennis op enige formele manier hadden gesystematiseerd. Dit werd overgelaten aan de oude Grieken. Wij hebben geen gedetailleerde kennis van die systematisering, behalve de bewering dat Thales (ca. 624 v. Chr. – ca. 546 v. Chr.) gaven de eerste ‘bewijzen’ van meetkundige feiten die het begin van de deductieve meetkunde markeerden. De Pythagorese School zette dit werk voort en Plato (428 v.Chr. -348 v. Chr.) put duidelijk uit het werk van eerdere wiskundigen wanneer hij meetkundige feiten noemt in zijn geschriften. De geometrische dialoog in zijn werk de Meno, waarin Socrates een slavin door een reeks logische gevolgtrekkingen tot een geometrische stelling laat komen, is het lezen waard. Als de oorsprong van de meetkunde onduidelijk is, is het’ eindproduct ‘ dat niet. Euclides (323-283 v.Chr.), schrijvend in Alexandrië, produceerde een opmerkelijk werk, genaamd de elementen, dat het standaard leerboek in de meetkunde bleef voor meer dan 2000 jaar. In dit werk beschrijft Euclides een aantal definities (zoals voor punten en lijnen), postulaten en gemeenschappelijke begrippen. (Tegenwoordig noemen we ze axioma ‘ s. Hieruit ontwikkelde hij logischerwijs, in een zeer zorgvuldig gekozen volgorde, een groot aantal stellingen die we gewoonlijk de Euclidische meetkunde noemen. Er zijn een aantal andere meetkundige resultaten, zoals de stelling van Pappus, die werden ontdekt na Euclides, maar deze worden over het algemeen niet behandeld in de middelbare school. Een van de vijf postulaten van Euclides was niet zo duidelijk waar als de anderen leken te zijn. Een versie ervan, bekend als Playfair ‘ s axioma stelt dat: Gegeven een regel  en een punt P, niet op
en een punt P, niet op  , is er één en slechts één lijn parallel aan
, is er één en slechts één lijn parallel aan  door P. In de 19e eeuw stelde een aantal wiskundigen de vraag ‘ Wat gebeurt er als we dit postulaat ontkennen?”Dit wordt gedaan door aan te nemen dat er ofwel geen dergelijke parallelle lijn is, ofwel door te zeggen dat er meer dan een dergelijke lijn is. Dit leidde tot de ontwikkeling van niet-Euclidische meetkunden, waarvan er één een van de goede modellen voor het universum bleek te zijn.
door P. In de 19e eeuw stelde een aantal wiskundigen de vraag ‘ Wat gebeurt er als we dit postulaat ontkennen?”Dit wordt gedaan door aan te nemen dat er ofwel geen dergelijke parallelle lijn is, ofwel door te zeggen dat er meer dan een dergelijke lijn is. Dit leidde tot de ontwikkeling van niet-Euclidische meetkunden, waarvan er één een van de goede modellen voor het universum bleek te zijn.
toepassingen
in zeer reële zin vormen meetkunde en meetkundige intuïtie de onderbouwing van alle
wiskunde − meetkunde leidt tot coördinerende meetkunde die leidt tot calculus en
al haar vele toepassingen − en is dus cruciaal in het curriculum. Op een meer praktisch niveau zijn bouwers, landmeters, ingenieurs en architecten al eeuwenlang intensief gebruik van geometrie en geometrische ideeën. Meer recentelijk, met de ontwikkeling van computers, hebben grafische kunstenaars en webdesigners zich aangesloten bij deze groep mensen die geometrie nodig hebben en gebruiken in hun werk. Op de vraag onlangs hoe nuttig geometrie is, Jim Kelly, een toegepaste wetenschapper zei:… geometrie is een belangrijk onderdeel van ontwerp, tekening en computermodellering. Het wordt ook vaak gebruikt in … natuurkunde en andere natuurwetenschappen cursussen als onderdeel van het begrijpen van de effecten van belastingen op structuren en balanceerpunten(zwaartepunt) voor samengestelde vaste stoffen. In chemie, is het begrijpen van de meetkunde van een molecuul verwant aan het begrijpen van de eigenschappen van substanties. Er bestaan nog veel meer voorbeelden. (van Ask a Scientist website.)
geschiedenis van de wiskunde: Een inleiding, 3e editie, Victor J. Katz, Addison-Wesley, (2008)
geschiedenis van de wiskunde, D. E. Smith, Dover publications New York, (1958)
antwoorden op oefeningen
oefening 1
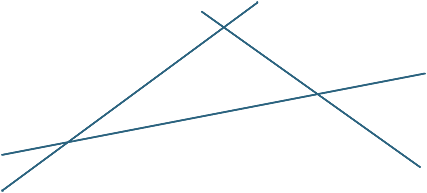
OEFENING 2
De punten collineair
OEFENING 3
60°
OEFENING 4
![]() DBA = 102° (overeenkomstige hoeken, AB||CD)
DBA = 102° (overeenkomstige hoeken, AB||CD)
![]() BAC = 78° (co-hoeken, AC||BD)
BAC = 78° (co-hoeken, AC||BD)
OEFENING 5
α = 65°![]() (overeenkomstige hoeken, AC||BM)
(overeenkomstige hoeken, AC||BM)
β = 80°![]() (alternatieve hoeken, AC||BM)
(alternatieve hoeken, AC||BM)
γ + β = 115°![]() (co-hoeken, AC||BM)
(co-hoeken, AC||BM)
Daarom, γ = 35°
(Dit is de structuur voor een bewijs van het resultaat dat de hoek som van een driehoek is 180°)
oefening 6
α = 60 °
oefening 7
a![]() een vierhoek met elk van de binnenhoeken een rechte hoek is een rechthoek.
een vierhoek met elk van de binnenhoeken een rechte hoek is een rechthoek.
Converse: elke binnenhoek van een rechthoek is een rechte hoek.
b![]() een rechthoek is een vierkant
een rechthoek is een vierkant
omgekeerd: een vierkant is een rechthoek
c![]() de hoek som van de binnenhoeken van een driehoek is 200°
de hoek som van de binnenhoeken van een driehoek is 200°
omgekeerd: een veelhoek waarvoor de som van de binnenhoek 200° is, is een driehoek.
oefening 8
α = 50°
oefening 9
we verwijzen naar hetzelfde diagram.
plaats een punt H op de lijn EF links van E.
![]() CBE =
CBE = ![]() BEH
BEH
als BC en EF niet parallel zijn, trek dan BD parallel aan EF.
aangezien BD en EF parallel zijn, ![]() EBD =
EBD = ![]() BEH, wat duidelijk onmogelijk is tenzij de regels BC en BD hetzelfde zijn.
BEH, wat duidelijk onmogelijk is tenzij de regels BC en BD hetzelfde zijn.
vandaar dat de regels BC en EF parallel zijn.
oefening 10
360°
het Improving Mathematics Education in Schools (TIMES) project 2009-2011 werd gefinancierd door het Australische ministerie van onderwijs, werkgelegenheid en Werkplekrelaties.
de hier geuite meningen zijn die van de auteur en komen niet noodzakelijk overeen met die van het Australische ministerie van onderwijs, werkgelegenheid en arbeidsverhoudingen.
© the University Of Melbourne namens het International Centre of Excellence for Education in Mathematics (Ice-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (tenzij anders aangegeven). Dit werk valt onder de Creative Commons Naamsvermelding-NietCommercieel-GelijkDelen 3.0 Unported licentie.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()