4.2 Het schatten van de coëfficiënten van Het lineaire regressiemodel

in de praktijk zijn het intercept $\beta_0$ en de helling $\beta_1$ van de populatieregressielijn onbekend. Daarom moeten we gegevens gebruiken om beide onbekende parameters in te schatten. Hieronder zal een voorbeeld uit de echte wereld worden gebruikt om aan te tonen hoe dit wordt bereikt. We willen testscores relateren aan de student-leraar ratio ‘ s gemeten in Californische scholen. De testscore is het district-brede gemiddelde van lezen en wiskunde scores voor vijfde klassers. Ook hier wordt de klasgrootte gemeten als het aantal leerlingen gedeeld door het aantal leraren (de student-Leraar verhouding). Wat betreft de gegevens, de California School data set (CASchools) wordt geleverd met een R pakket genaamd AER, een acroniem voor Applied Econometrics met R (Kleiber and Zeileis 2020). Na het installeren van het pakket met install.pakketten (“AER”) en het koppelen met library(AER) de dataset kan worden geladen met behulp van de functie data ().

## # install the AER package (once)## install.packages("AER")## ## # load the AER packagelibrary(AER)# load the the data set in the workspacedata(CASchools)

zodra een pakket is geÃ nstalleerd is het beschikbaar voor gebruik bij andere gelegenheden wanneer aangeroepen met library () — er is geen noodzaak om te draaien install.packages () opnieuw!

het is interessant om te weten met welk soort object we te maken hebben.class () geeft de klasse van een object terug. Afhankelijk van de klasse van een object gedragen sommige functies (bijvoorbeeld plot() en summary()) zich anders.

laten we de klasse van het object CASchools controleren.

class(CASchools)#> "data.frame"

het blijkt dat CASchools van klasse data is.frame dat is een handig formaat om mee te werken, vooral voor het uitvoeren van regressieanalyse.

met behulp van head() krijgen we een eerste overzicht van onze gegevens. Deze functie toont alleen de eerste 6 rijen van de gegevensset die een overvolle console-uitvoer voorkomt.

druk op ctrl + L om de console te wissen. Dit commando verwijdert alle code die door u is ingetypt en uitgevoerd of door R-functies naar de console is afgedrukt. Het goede nieuws is dat al het andere onaangeroerd blijft. U noch losse gedefinieerde variabelen etc. noch de code geschiedenis. Het is nog steeds mogelijk om eerder uitgevoerde R commando ‘ s terug te roepen met behulp van de toetsen omhoog en omlaag. Als u in RStudio werkt, drukt u op ctrl + Up op uw toetsenbord (CMD + Up op een Mac) om een lijst met eerder ingevoerde opdrachten te bekijken.

head(CASchools)#> district school county grades students teachers#> 1 75119 Sunol Glen Unified Alameda KK-08 195 10.90#> 2 61499 Manzanita Elementary Butte KK-08 240 11.15#> 3 61549 Thermalito Union Elementary Butte KK-08 1550 82.90#> 4 61457 Golden Feather Union Elementary Butte KK-08 243 14.00#> 5 61523 Palermo Union Elementary Butte KK-08 1335 71.50#> 6 62042 Burrel Union Elementary Fresno KK-08 137 6.40#> calworks lunch computer expenditure income english read math#> 1 0.5102 2.0408 67 6384.911 22.690001 0.000000 691.6 690.0#> 2 15.4167 47.9167 101 5099.381 9.824000 4.583333 660.5 661.9#> 3 55.0323 76.3226 169 5501.955 8.978000 30.000002 636.3 650.9#> 4 36.4754 77.0492 85 7101.831 8.978000 0.000000 651.9 643.5#> 5 33.1086 78.4270 171 5235.988 9.080333 13.857677 641.8 639.9#> 6 12.3188 86.9565 25 5580.147 10.415000 12.408759 605.7 605.4

We zien dat de dataset uit tal van variabelen bestaat en dat de meeste ervan numeriek zijn.

overigens: een alternatief voor class() en head() is str (), dat wordt afgeleid uit ‘structure’ en een uitgebreid overzicht van het object geeft. Probeer!

terugkerend naar CASchools, zijn de twee variabelen waarin we geïnteresseerd zijn (d.w.z., gemiddelde testscore en de student-Leraar verhouding) zijn niet inbegrepen. Het is echter mogelijk om beide uit de verstrekte gegevens te berekenen. Om de student-leraar ratio ‘ s te verkrijgen, delen we gewoon het aantal studenten door het aantal leraren. De gemiddelde testscore is het rekenkundig gemiddelde van de testscore voor het lezen en de score van de wiskundetoets. De volgende code chunk laat zien hoe de twee variabelen kunnen worden geconstrueerd als vectoren en hoe ze worden toegevoegd aan CASchools.

# compute STR and append it to CASchoolsCASchools$STR <- CASchools$students/CASchools$teachers # compute TestScore and append it to CASchoolsCASchools$score <- (CASchools$read + CASchools$math)/2

als we head(CASchools) opnieuw zouden lopen zouden we de twee variabelen van belang vinden als extra kolommen genaamd STR en score (Controleer dit!).

tabel 4.1 uit het handboek geeft een samenvatting van de verdeling van de testscores en de verhouding tussen student en leraar. Er zijn verschillende functies die kunnen worden gebruikt om vergelijkbare resultaten te produceren, bijv.,

mean () (berekent het rekenkundig gemiddelde van de opgegeven getallen),
sd () (berekent de standaardafwijking van het monster),
kwantiel () (geeft een vector van de gespecificeerde monster kwantielen voor de gegevens).

de volgende code chunk laat zien hoe dit te bereiken. Eerst berekenen we samenvattende statistieken over de kolommen STR en score van CASchools. Om een mooie output te krijgen verzamelen we de metingen in een data.frame genaamd DistributionSummary.

# compute sample averages of STR and scoreavg_STR <- mean(CASchools$STR) avg_score <- mean(CASchools$score)# compute sample standard deviations of STR and scoresd_STR <- sd(CASchools$STR) sd_score <- sd(CASchools$score)# set up a vector of percentiles and compute the quantiles quantiles <- c(0.10, 0.25, 0.4, 0.5, 0.6, 0.75, 0.9)quant_STR <- quantile(CASchools$STR, quantiles)quant_score <- quantile(CASchools$score, quantiles)# gather everything in a data.frame DistributionSummary <- data.frame(Average = c(avg_STR, avg_score), StandardDeviation = c(sd_STR, sd_score), quantile = rbind(quant_STR, quant_score))# print the summary to the consoleDistributionSummary#> Average StandardDeviation quantile.10. quantile.25. quantile.40.#> quant_STR 19.64043 1.891812 17.3486 18.58236 19.26618#> quant_score 654.15655 19.053347 630.3950 640.05000 649.06999#> quantile.50. quantile.60. quantile.75. quantile.90.#> quant_STR 19.72321 20.0783 20.87181 21.86741#> quant_score 654.45000 659.4000 666.66249 678.85999

wat de steekproefgegevens betreft, gebruiken we plot (). Dit stelt ons in staat om kenmerken van onze gegevens te detecteren, zoals uitschieters die moeilijker te ontdekken zijn door te kijken naar louter getallen. Deze keer voegen we enkele extra argumenten toe aan de Call of plot().

het eerste argument in onze Call of plot (), score ~ STR, is opnieuw een formule die variabelen op de Y – en de x-as aangeeft. Echter, deze keer worden de twee variabelen niet opgeslagen in afzonderlijke vectoren, maar zijn kolommen van CASchools. Daarom zou R ze niet vinden zonder dat de argumentgegevens correct zijn gespecificeerd. de gegevens moeten in overeenstemming zijn met de naam van de gegevens.frame waartoe de variabelen behoren, in dit geval CASchools. Andere argumenten worden gebruikt om het uiterlijk van de plot te veranderen: terwijl main een titel toevoegt, voegen xlab en ylab aangepaste labels toe aan beide assen.

plot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)")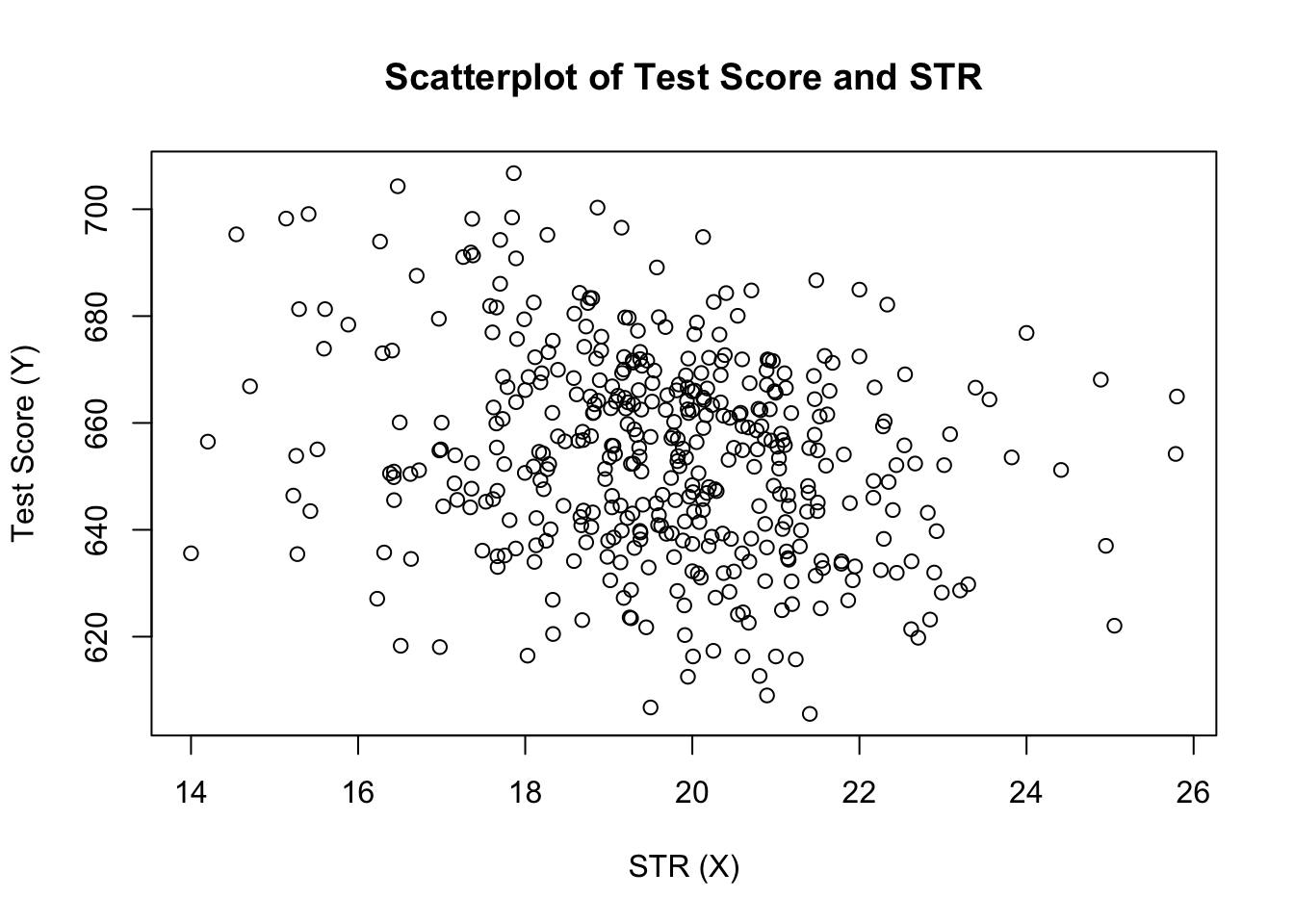

de plot (figuur 4.2 in het boek) toont de verstrooiing van alle waarnemingen op de student-Leraar verhouding en test score. We zien dat de punten sterk verspreid zijn, en dat de variabelen negatief gecorreleerd zijn. Dat wil zeggen, we verwachten lagere testscores in grotere klassen te observeren.

de functie cor () (zie ?cor voor meer informatie) kan worden gebruikt om de correlatie tussen twee numerieke vectoren te berekenen.

cor(CASchools$STR, CASchools$score)#> -0.2263627

zoals de scatterplot al suggereert, is de correlatie negatief, maar eerder zwak.

de taak waar we nu voor staan is het vinden van een regel die het beste bij de gegevens Past. Natuurlijk konden we gewoon vasthouden aan grafische inspectie en correlatieanalyse en vervolgens de best passende lijn selecteren door te kijken. Dit zou echter nogal subjectief zijn: verschillende waarnemers zouden verschillende regressielijnen trekken. Daarom zijn we geïnteresseerd in technieken die minder willekeurig zijn. Een dergelijke techniek wordt gegeven door gewone kleinste kwadraten (OLS) schatting.

De gewone kleinste-kwadraten schatter

de OLS-schatter kiest de regressiecoëfficiënten zodanig dat de geschatte regressielijn zo “dicht” mogelijk bij de waargenomen gegevenspunten ligt. Hier wordt nabijheid gemeten door de som van de kwadraatfouten die zijn gemaakt bij het voorspellen van $Y$ gegeven $X$. Laat $b_0$ en $b_1$ enkele schatters zijn van $\beta_0$ en $\beta_1$. Dan kan de som van kwadraat schattingsfouten worden uitgedrukt als

de OLS-schatter in het eenvoudige regressiemodel is het paar schatters voor onderschepping en helling dat de bovenstaande uitdrukking minimaliseert. De afleiding van de OLS-schatters voor beide parameters wordt weergegeven in aanhangsel 4.1 van het boek. De resultaten zijn samengevat in hoofdconcept 4.2.

De OLS-Schatter, de Voorspelde Waarden, en de Residuen

De OLS-schatters van de helling $\beta_1$ en het snijpunt $\beta_0$ in de eenvoudige lineaire regressie model zijn\De OLS-de voorspelde waarden $\widetilde{Y}_i$ en de residuen $\hat{u}_i$ zijn\

De geschatte intercept $\hat{\beta}_0$, de helling parameter $\hat{\beta}_1$ en de resten $\left(\hat{u}_i\right)$ zijn berekend op basis van een steekproef van $n$ waarnemingen van $X_i$ en $Y_i$, $i$, $…$, $en$. Dit zijn schattingen van de onbekende populatie-onderschepping $\left (\beta_0 \ right)$, helling $\left(\beta_1\right)$, en foutterm $(u_i)$.

de bovenstaande formules zijn op het eerste gezicht misschien niet erg intuïtief. De volgende interactieve applicatie is bedoeld om u te helpen de mechanica van OLS te begrijpen. U kunt waarnemingen toevoegen door te klikken in het coördinatenstelsel waar de gegevens worden weergegeven door punten. Zodra twee of meer waarnemingen beschikbaar zijn, berekent de toepassing een regressielijn met behulp van OLS en enkele statistieken die in het rechterpaneel worden weergegeven. De resultaten worden bijgewerkt als u verdere waarnemingen toe te voegen aan het linker paneel. Een dubbelklik reset de toepassing, dat wil zeggen, alle gegevens worden verwijderd.

er zijn vele mogelijke manieren om $\hat{\beta}_0$ en $\hat{\beta}_1$ in R. bijvoorbeeld, we zouden de formules in sleutelconcept 4.2 kunnen implementeren met twee van R ‘ s meest basisfuncties: mean() en sum(). Voordat we dit doen voegen we de CASchools dataset toe.

attach(CASchools) # allows to use the variables contained in CASchools directly# compute beta_1_hatbeta_1 <- sum((STR - mean(STR)) * (score - mean(score))) / sum((STR - mean(STR))^2)# compute beta_0_hatbeta_0 <- mean(score) - beta_1 * mean(STR)# print the results to the consolebeta_1#> -2.279808beta_0#> 698.9329

Calling attach(CASchools) stelt ons in staat om een variabele in CASchools met zijn naam te adresseren: het is niet langer nodig om de $ operator te gebruiken in combinatie met de dataset: R kan de naam van de variabele direct evalueren.

R gebruikt het object in de gebruikersomgeving als dit object de naam van de variabele in een bijgevoegde database deelt. Het is echter beter om altijd onderscheidende namen te gebruiken om dergelijke (schijnbaar) ambivalenties te vermijden!

merk op dat we variabelen in de bijgevoegde dataset CASchools direct voor de rest van dit hoofdstuk adresseren!

natuurlijk zijn er nog meer handmatige manieren om deze taken uit te voeren. Aangezien OLS een van de meest gebruikte schattingstechnieken is, bevat R natuurlijk al een ingebouwde functie met de naam lm() (lineair model) die kan worden gebruikt om regressieanalyse uit te voeren.

het eerste argument van de te specificeren functie is, vergelijkbaar met plot(), de regressieformule met de basissyntaxis y ~ x waar y de afhankelijke variabele is en x de verklarende variabele. De argumentgegevens bepalen de gegevensverzameling die in de regressie moet worden gebruikt. We bekijken nu het voorbeeld uit het boek waar de relatie tussen de testscores en de klassengrootte wordt geanalyseerd. De volgende code gebruikt lm () om de resultaten in figuur 4.3 van het boek te repliceren.

# estimate the model and assign the result to linear_modellinear_model <- lm(score ~ STR, data = CASchools)# print the standard output of the estimated lm object to the console linear_model#> #> Call:#> lm(formula = score ~ STR, data = CASchools)#> #> Coefficients:#> (Intercept) STR #> 698.93 -2.28

laten we de geschatte regressielijn toevoegen aan de plot. Deze keer vergroten we ook het bereik van beide assen door de argumenten xlim en ylim in te stellen.

# plot the dataplot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)", xlim = c(10, 30), ylim = c(600, 720))# add the regression lineabline(linear_model)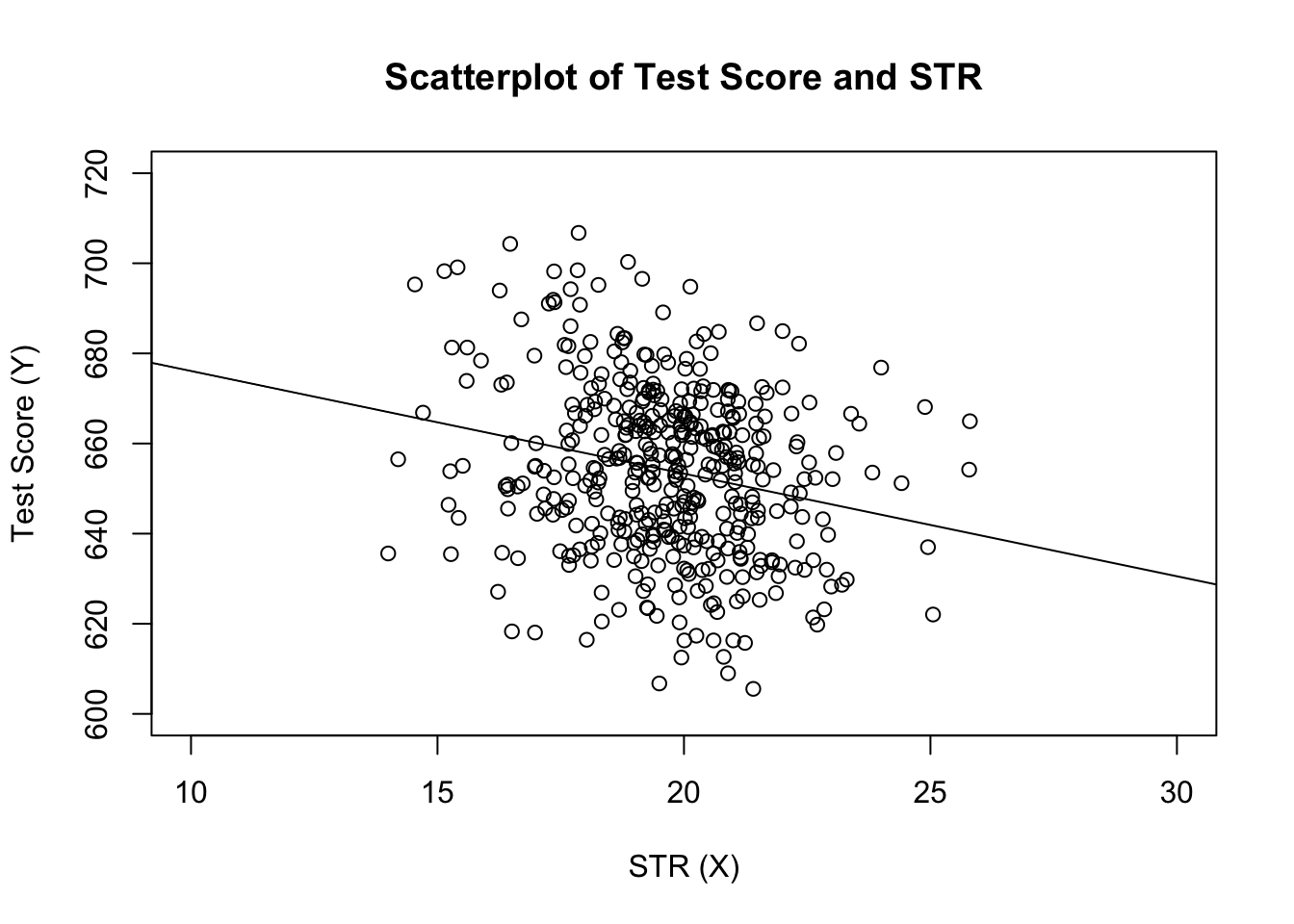

heb je gemerkt dat we deze keer de onderscheppings-en hellingsparameters niet hebben doorgegeven aan abline? Als u abline() aanroept op een object van klasse lm dat slechts één regressor bevat, tekent R de regressielijn automatisch!