vandaag zal een korte introductie zijn in circulaire statistieken (soms aangeduid als directionele statistieken). Circulaire statistieken is een interessante onderverdeling van statistieken waarbij waarnemingen als vectoren worden genomen rond een eenheidscirkel. Stel je bijvoorbeeld voor dat je de geboortetijden meet in een ziekenhuis over een cyclus van 24 uur, of de gerichte verspreiding van een groep trekdieren. Dit type gegevens is betrokken in een verscheidenheid gebieden, zoals ecologie, klimatologie, en biochemie. De aard van het meten van waarnemingen rond een eenheidscirkel vereist een andere benadering van het testen van hypothesen. Distributies moeten worden” gewikkeld ” rond de cirkel om van nut te zijn, en conventionele schatters zoals het steekproefgemiddelde of steekproefvariantie houden geen water.
In dit artikel zullen we Rao ‘ s spatiëring testen om de uniformiteit van een circulaire dataset te beoordelen. Dit is een basisprocedure en moet worden beschouwd als een inleiding tot het omgaan met circulaire gegevens.
aan de slag
we gaan een hypothese test uitvoeren op schildpadden, een kleine dataset bestaande uit de aankomsthoeken van 10 groene zeeschildpadden naar hun broedeiland. Ons doel is om te bepalen waar de aankomsthoeken tekenen van richting vertonen of meer indicatief zijn voor een willekeurige verstrooiing.Installeer eerst het circular pakket en voeg de turtles-dataset toe.
install.packages("circular")require(circular)attach(turtles)
plotten van de gegevens
het circular pakket bevat zijn eigen plotfunctie, plot.circular. Laten we de aankomsthoeken van de schildpadden bekijken.
plot.circular(arrival)
hier is het perceel: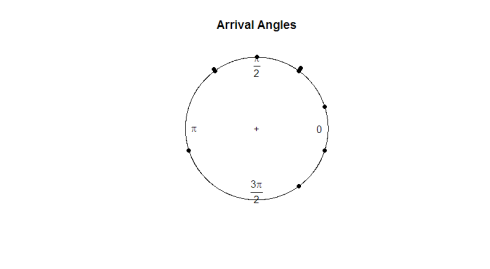
gezien de oogtest lijken de waarnemingen rond de cirkel gelijk te zijn. Als we een hypothese test willen uitvoeren om te bepalen of de gegevens echt uniform zijn, zullen we een teststatistiek moeten ontwikkelen die werkt met hoekgegevens.
Wat is een goede parameter voor ons om te gebruiken? Het nemen van het steekproefgemiddelde vertelt ons niet veel over de richting van de gegevens (180 graden is geen nuttig gemiddelde van 2 graden en 358 graden). In de volgende plot, observeren hoe het monster gemiddelde is van geen nut bij het vertegenwoordigen van de vorm of verspreiding van onze gegevens.
mean(arrival)plot.circular(mean(arrival)) 0.9120794
hier is het perceel: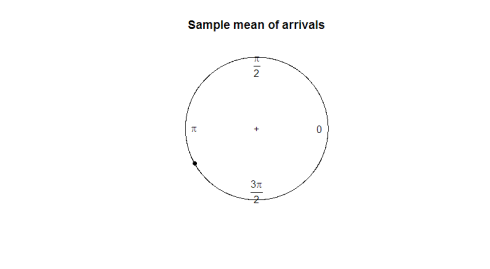
in plaats daarvan zullen we een methode gebruiken die de richting bepaalt door de gemiddelde ruimte tussen waarnemingen te meten. Deze test heet Rao ‘ s spatiëring Test.
Rao ’s Afstandstest
Rao’ s Afstandstest werd ontwikkeld om de uniformiteit van circulaire gegevens te beoordelen. Het gebruikt de ruimte tussen observaties om te bepalen of de gegevens significante richting tonen. Als de gegevens uniform zijn, moeten de waarnemingen gelijkmatig uit elkaar liggen.
hier is de teststatistiek \(u\) voor de Afstandstest van de Rao: $$U = 1/2 \ sum \ limits_{i = 1}^n| T_{i} – λ / $ $ waarbij \(λ = 360/ n, T_{i} = f_{i+1} – f_{i}\) en \(T_{n} =(360-f_{n})+f_{1}\)
in principe aggregeert de teststatistiek de afwijkingen tussen opeenvolgende punten, elk gewogen door het totale aantal waarnemingen in de dataset.
we zullen de functie rao.spacing.test() gebruiken om deze hypothesetest uit te voeren. Onze nulhypothese zegt dat de gegevens van een uniforme verdeling zijn, terwijl de alternatieve Staten dat de gegevens tekenen van richting vertonen. Laten we de test doen.
rao.spacing.test(arrival,alpha=.10) Rao's Spacing Test of Uniformity Test Statistic = 127.2689 Level 0.1 critical value = 161.23 Do not reject null hypothesis of uniformity
bij een teststatistiek van 127 die onder de kritische waarde van 161 valt, worden de gegevens in geen enkele richting significant beïnvloed. We kunnen de hypothese niet verwerpen dat de aankomsten van de schildpadden van een uniforme verdeling zijn.
conclusie
met de Rao-test werd bepaald dat de gegevens geen tekenen van richtingstrends vertoonden. We kunnen de nulhypothese van uniformiteit niet verwerpen en zullen uniformiteit aannemen met betrekking tot de richting van aankomst. Hoewel dit bericht was een relatief eenvoudige tutorial, veel mensen in de data science gemeenschap hebben niet gewerkt met circulaire gegevens voor. Het is een interessante subtopie om in te duiken, evenals een jong gebied van statistieken dat nog steeds in ontwikkeling is.
slotopmerkingen
ik zou graag een krediet willen verlenen aan S. Rao Jammalamadaka PhD, van de Universiteit van Californië, Santa Barbara, en zijn leerboek “Topics in Circular Statistics” voor het aanwakkeren van mijn interesse in circulaire statistieken.