feltételezett tudás
a hallgatók széles körű informális tapasztalattal rendelkeznek a geometriával kapcsolatban a korábbi években, és ez jó intuitív alapot nyújt a geometria szisztematikusabb megközelítéséhez a 7-10. A modul szempontjából releváns F−6 évek konkrét témái a következők:
- az iránytűk és vonalzók használata és a geometriai ábrák gondos rajzolása.
- a szögek típusai, beleértve legalább a derékszögeket, a hegyesszögeket, a tompaszögeket és a
reflexszögeket. - háromszögek, beleértve az egyenlő szárú és egyenlő oldalú háromszögek informális bevezetését.
- négyszögek, beleértve a négyzetek, téglalapok, paralelogrammok, trapézok és rombuszok informális bevezetését.
- informális tapasztalat fordításokkal, reflexiókkal, forgatásokkal és nagyításokkal,
és szimmetriával olyan tevékenységek összefüggésében, mint például egy egyenlő szárú háromszög, téglalap vagy rombusz hajtogatása.
Motiváció
 a geometria a körülöttünk lévő világ modellezésére szolgál. A házak tetejére néző kilátás háromszögeket, trapézokat és téglalapokat tár fel, míg a járdák és a fürdőszobák csempézési mintái hatszögeket, ötszögeket, háromszögeket és négyzeteket használnak.
a geometria a körülöttünk lévő világ modellezésére szolgál. A házak tetejére néző kilátás háromszögeket, trapézokat és téglalapokat tár fel, míg a járdák és a fürdőszobák csempézési mintái hatszögeket, ötszögeket, háromszögeket és négyzeteket használnak.
építők, burkolók, építészek, grafikusok és webdesignerek rutinszerűen használnak geometriai ötleteket munkájuk során. Az ilyen geometriai objektumok osztályozása és tulajdonságaik tanulmányozása nagyon fontos. A geometriának számos alkalmazása van a művészetben.
ahogy az aritmetikának is vannak számai, mint alapvető tárgyai, úgy a pontok, vonalak és körök is a síkgeometria alapvető építőkövei.
a középiskolai geometriában számos olyan intuitív ötlettel (pontokkal, vonalakkal és szögekkel) kezdjük, amelyeket egyáltalán nem könnyű pontosan meghatározni, majd néhány definíció következik (függőlegesen ellentétes szögek, párhuzamos vonalak stb.), és ezekből fontos tényeket vonunk le, amelyeket gyakran tételeknek neveznek. A középiskolában a szigor szintjének lassan kell fejlődnie egyik évről a másikra, de minden szakaszban nagyon fontos a világos megfogalmazás, amelyet hangsúlyozni kell.
így geometria lehetőséget ad a diákoknak, hogy fejlesszék a geometriai intuíció, amely alkalmazások számos területen az élet, valamint megtanulják, hogyan kell építeni logikai érvek és levonások olyan környezetben, amely a legtöbb esetben független
szám.
tartalom
pontok és vonalak
a síkgeometriában a legegyszerűbb objektumok a pontok és vonalak. Mivel annyira egyszerűek, nehéz pontos meghatározásokat adni róluk, ezért ehelyett arra törekszünk, hogy a hallgatóknak durva leírást adjunk tulajdonságaikról, amelyek összhangban vannak intuíciónkkal. Egy pont egy pozíciót jelöl, de nincs mérete. A gyakorlatban, amikor egy pontot rajzolunk, annak egyértelműen meghatározott szélessége van, de képzeletünkben egy pontot képvisel. Egy vonalnak nincs szélessége, és mindkét irányban végtelenül kiterjed. Amikor egy vonalat rajzolunk, annak szélessége és vége van, tehát valójában nem egy vonal, hanem egy vonalat képvisel a képzeletünkben. Ha két különböző a és B pont van, akkor van egy (és csak egy) vonal, amely mindkét ponton áthalad. Nagybetűket használunk a pontokra és a névsorokra való hivatkozáshoz vagy két pont megadásával a vonalon, vagy kis betűkkel, például  és m. így az alábbi sort AB vonalnak vagy
és m. így az alábbi sort AB vonalnak vagy  vonalnak nevezzük.
vonalnak nevezzük.

két különböző vonal esetén két lehetőség van: vagy egy ponton találkoznak, vagy soha nem találkoznak, függetlenül attól, hogy milyen messzire vannak meghosszabbítva (vagy előállítva). Azokat a vonalakat, amelyek soha nem találkoznak, párhuzamosnak nevezzük. A második ábrán AB ||CD-t írunk.
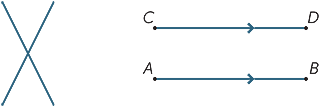
három (vagy több) pontot, amelyek egyenes vonalban fekszenek, kollineárisnak nevezzük.
három (vagy több) vonalat, amelyek egy ponton találkoznak, egyidejűnek nevezzük.
|
|
|
| kollineáris |
egyidejű |
1. gyakorlat
rajzoljon három nem párhuzamos vonalat úgy, hogy kettő ne legyen párhuzamos.
2. gyakorlat
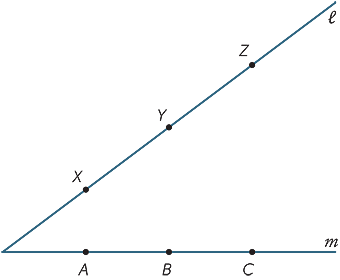
készítsen nagy másolatot az alábbi ábráról. Az X, Y, Z pontok a  vonal bármely pontja, és az A ,B, C az M vonal bármely pontja. csatlakozzon AY-hoz és XB hívja a kereszteződésüket R. csatlakozzon BZ-hez és YC-hez, és hívja a kereszteződésüket P. csatlakozzon CX-hez és ZA-hoz, és hívja a kereszteződésüket Q. mit észlel a P, Q, R pontokról? (Ezt az eredményt Pappus tételnek hívják, KR.u. 340.)
vonal bármely pontja, és az A ,B, C az M vonal bármely pontja. csatlakozzon AY-hoz és XB hívja a kereszteződésüket R. csatlakozzon BZ-hez és YC-hez, és hívja a kereszteződésüket P. csatlakozzon CX-hez és ZA-hoz, és hívja a kereszteződésüket Q. mit észlel a P, Q, R pontokról? (Ezt az eredményt Pappus tételnek hívják, KR.u. 340.)
intervallumok, sugarak és szögek
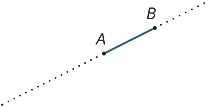 tegyük fel, hogy A és B egy vonal két pontja. A
tegyük fel, hogy A és B egy vonal két pontja. A
AB intervallum az A és B közötti vonal része, beleértve a két végpontot is.
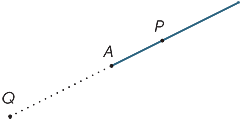 a diagram A pontja a vonalat két részre osztja, amelyeket sugaraknak neveznek. Az AP sugár az a sugár, amely tartalmazza a P pontot (és az A pontot).
a diagram A pontja a vonalat két részre osztja, amelyeket sugaraknak neveznek. Az AP sugár az a sugár, amely tartalmazza a P pontot (és az A pontot).
Szögek
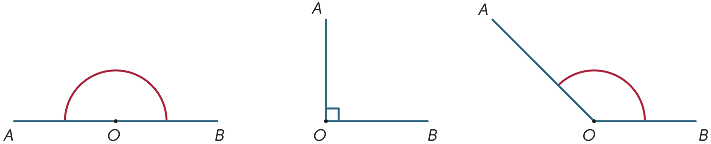
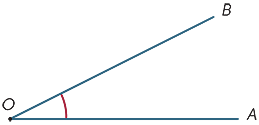
 az ábrán az OA és OB sugarak közötti árnyékolt területet AOB szögnek vagy Boa szögnek nevezzük. A
az ábrán az OA és OB sugarak közötti árnyékolt területet AOB szögnek vagy Boa szögnek nevezzük. A ![]() szögjelet így írjuk
szögjelet így írjuk ![]() AOB.
AOB.
 a külső árnyékolt területet az OA és az OB által alkotott reflexszögnek nevezzük. Legtöbbször, hacsak nem adjuk meg a reflex szót, minden szögünk a sugarak közötti területre vonatkozik, nem pedig azokon kívül.
a külső árnyékolt területet az OA és az OB által alkotott reflexszögnek nevezzük. Legtöbbször, hacsak nem adjuk meg a reflex szót, minden szögünk a sugarak közötti területre vonatkozik, nem pedig azokon kívül.
a szög mérete
 képzelje el, hogy az OB sugár az O pont körül forog, amíg az OA mentén fekszik. Az esztergálás mértékét az AOB szög méretének nevezzük. Hasonlóképpen meghatározhatjuk a reflex szög méretét.
képzelje el, hogy az OB sugár az O pont körül forog, amíg az OA mentén fekszik. Az esztergálás mértékét az AOB szög méretének nevezzük. Hasonlóképpen meghatározhatjuk a reflex szög méretét.
gyakran használunk kis görög betűket, 6, XNUMX, XNUMX,… a szög méretének ábrázolása.
az egy teljes forradalomnak megfelelő szög méretét (a babiloniak) 360 egyenlő részre osztották, amelyeket fokoknak nevezünk. (Valószínűleg 360-at választottak, mivel ez közel volt az egy év napjainak számához.) Ezért az egyenes szög mérete 180, a derékszög mérete pedig 90 milliméter. Más szögek (megközelítőleg) mérhetők egy szögmérő segítségével.
|
|
||
| egyenes szög | derékszög |
tompaszög |
a szögeket méretük szerint osztályozzák. Azt mondjuk, hogy egy szöget méret α akut
(egy szó, jelentése ‘éles’), ha 0° < α < 90°, α tompa (egy szó, jelentése ‘nyers’), ha
90° < α < 180° α reflex, ha 180° < α < 360°.
mivel a szögmérőnek két skálája van, a hallgatóknak óvatosnak kell lenniük a rajzolás és a
szögmérés során. Érdemes gyakorolni egy szögmérőt, hogy rajzoljon néhány szöget, például 30°, 78°, 130°, 163°.
Gyakorlat 3
 hajtson be egy A4-es papírlapot, amely megfelel az (átlósan) ellentétes sarkoknak. Rajzolj egy vonalat a kialakult ránc mentén, és mérd meg a ránc és az oldal közötti szögeket.
hajtson be egy A4-es papírlapot, amely megfelel az (átlósan) ellentétes sarkoknak. Rajzolj egy vonalat a kialakult ránc mentén, és mérd meg a ránc és az oldal közötti szögeket.
a fenti gyakorlatban a két szög együtt egyenes vonalat képez, és így 180 db-ot ad hozzá. Két olyan szöget nevezünk kiegészítő szögeknek, amelyek 180-at adnak hozzá, így a 45 és 135-öt kiegészítő szögeknek nevezzük.
két olyan szöget, amely 90-et ad hozzá, komplementer szögnek nevezünk; így a 23 és a 67-et
komplementer szögnek nevezzük.
szögek egy ponton
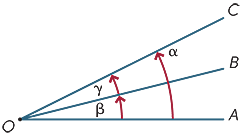 két szög egy ponton azt mondják, hogy szomszédos, ha közös sugárral rendelkeznek. Ezért a diagramban
két szög egy ponton azt mondják, hogy szomszédos, ha közös sugárral rendelkeznek. Ezért a diagramban ![]() AOB és
AOB és ![]() BOC szomszédos.
BOC szomszédos.
szomszédos szögek adhatók hozzá, így a diagramban
6 = + + XNUMX.
ha két vonal keresztezi egymást, négy szög alakul ki a metszéspontban.
az ábrán a ![]() AOX és
AOX és ![]() BOY jelölésű szögeket függőlegesen ellentétesnek nevezzük.
BOY jelölésű szögeket függőlegesen ellentétesnek nevezzük.
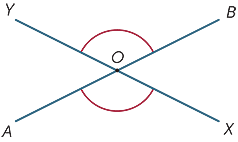 óta
óta
-
 az AOX a
az AOX a  doboz (egyenes szög) kiegészítése.
doboz (egyenes szög) kiegészítése. -
 fiú is a kiegészítő
fiú is a kiegészítő  doboz (egyenes szög),
doboz (egyenes szög),
megállapíthatjuk, hogy ezek a függőlegesen ellentétes szögek, ![]() AOX és
AOX és ![]() BOY egyenlőek. Így van az első
BOY egyenlőek. Így van az első
fontos geometriai állításunk:
függőlegesen ellentétes szögek egyenlőek.
a geometria (és általában a matematika) eredményét gyakran tételnek nevezik. A tétel fontos állítás, amelyet logikai dedukcióval lehet bizonyítani. A fenti érv a tétel bizonyítéka; néha a bizonyítékokat formálisan mutatják be a tétel kijelentése után.
 ha két vonal úgy metszik egymást, hogy mind a négy szög derékszögű, akkor a vonalak merőlegesek.
ha két vonal úgy metszik egymást, hogy mind a négy szög derékszögű, akkor a vonalak merőlegesek.
szögek egy ponton-Geometriai argumentumok
a geometriai argumentumokban a következő okok használhatók:
- a szomszédos szögek hozzáadhatók vagy kivonhatók.
- a szögek egy forradalomban 360 db-ot tesznek ki.
- az egyenes vonalú szögek 180 db-ot tesznek ki.
- függőlegesen ellentétes szögek egyenlőek.
keresztirányú és párhuzamos vonalak
 a keresztirányú egy olyan vonal, amely két másik sorral találkozik.
a keresztirányú egy olyan vonal, amely két másik sorral találkozik.
megfelelő szögek
különböző szögek vannak kialakítva a keresztirányban. Az alábbi ábrákon a két megjelölt szöget megfelelő szögeknek nevezzük.
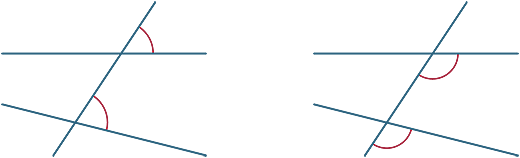
 most megnézzük, mi történik, ha a keresztirányban levágott két vonal párhuzamos.
most megnézzük, mi történik, ha a keresztirányban levágott két vonal párhuzamos.
Inituitively, ha a szög α nagyobb volt, mint a β akkor CD-át az AB, hogy a bal, F, illetve, ha ez kevesebb, mint β, akkor a kereszt, hogy a F. mivel a vonalak nem kereszt egyáltalán, α sem kevesebb, sem több, mint a β így egyenlő β.
Alternatív megoldásként képzelje el, hogy a szöget lefordítja QGD GF mentén, amíg G egybeesik F-vel. Ez a megfigyelés arra enged következtetni, hogy:
a párhuzamos vonalakból kialakított megfelelő szögek egyenlőek.
ezt az eredményt nem tudjuk bizonyítani, bár megmutattuk, hogy geometriailag elfogadható. Ezt a geometria axiómájaként fogjuk elfogadni. Az axióma olyan állítás, amelyet nem tudunk bizonyítani, de intuitív módon ésszerű. Ne feledje, hogy sok olyan tény, amelyet már megállapítottunk, például: szomszédos szögek adhatók hozzá, két pont pedig egy vonalat határoz meg stb., szintén axiómák, bár ezeket kifejezetten nem mondtuk ki ilyen módon.
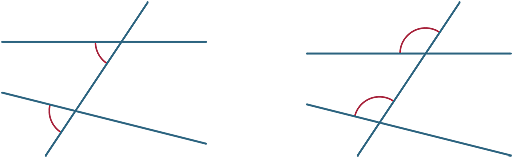
alternatív szögek
az egyes diagramokban a két megjelölt szöget alternatív szögeknek nevezzük (mivel a keresztirányú alternatív oldalán vannak).

 ha az AB és a CD vonalak párhuzamosak, akkor az alternatív szögek egyenlőek. Ez az eredmény most bizonyítható.
ha az AB és a CD vonalak párhuzamosak, akkor az alternatív szögek egyenlőek. Ez az eredmény most bizonyítható.
![]() dgq = (megfelelő szögek, AB / / CD)
dgq = (megfelelő szögek, AB / / CD)
![]() DGQ = (függőlegesen ellentétes szögek a G-nél)
DGQ = (függőlegesen ellentétes szögek a G-nél)
tehát a (z) stb.
összefoglalva:
a párhuzamos vonalakból kialakított alternatív szögek egyenlőek.
Co-belső szögek
végül az alábbi diagramon a két megjelölt szöget co-belső szögeknek nevezzük, és a keresztirányú ugyanazon oldalán fekszenek.

ha az AB és a CD egyenesek párhuzamosak, akkor nyilvánvaló, hogy a Ko-belső szögek nem egyenlőek, de kiderül, hogy kiegészítőek, Vagyis összegük 180 hektár.
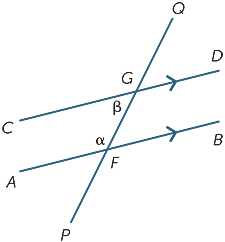 ez egy olyan eredmény, amelyet szintén könnyű bizonyítani:
ez egy olyan eredmény, amelyet szintén könnyű bizonyítani:
![]() BFG = (alternatív szögek, AB ||CD)
BFG = (alternatív szögek, AB ||CD)
(egyenes szög F-nél)
összefoglalva:
a párhuzamos vonalakból kialakított belső szögek kiegészítőek.
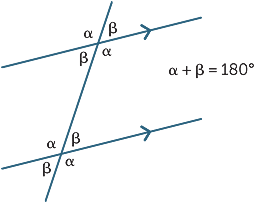 a három eredmény
a három eredmény
a következő diagrammal foglalható össze:
numerikus példák
a diagram szögeire vonatkozó információk alapján a fenti eredmények segítségével megállapíthatjuk a diagram többi szögének méretét. Ez egy egyszerű, de nagyon fontos készség, amelyet gyakran informálisan szög üldözésnek neveznek. A problémák megoldása során a lépések sorrendje nem mindig egyedi. Lehet, hogy több különböző, de ugyanolyan érvényes megközelítés létezik.
például a következő ábrán a BAC szög méretét keressük.

![]() DCA = 102 (váltakozó szögek, AC|BD)
DCA = 102 (váltakozó szögek, AC|BD)
![]() BAC = 78 (belső szögek, AB / / CD)
BAC = 78 (belső szögek, AB / / CD)
4. gyakorlat
használjon alternatív lépéseket a ![]() BAC megtalálásához.
BAC megtalálásához.
Gyakorlat 5
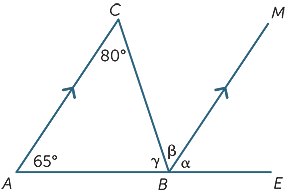 csak a párhuzamos vonalak tulajdonságait használva keresse meg (indoklással) a hiányzó szögeket a következő ábrán.
csak a párhuzamos vonalak tulajdonságait használva keresse meg (indoklással) a hiányzó szögeket a következő ábrán.
6. gyakorlat
keresse meg a következő ábrán a ++ értékét.
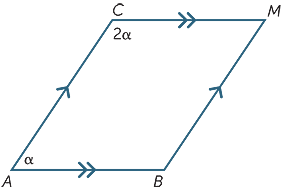
Converse állítások
a matematikában sok állításnak van egy fordítottja, amelyben a következmény ellentétes irányba megy. Például a
‘minden páros szám 0, 2, 4, 6 vagy 8-ra végződik.’
van converse
‘ minden szám, amely 0-ra, 2-re, 4-re, 6-ra vagy 8-ra végződik, páros.’
ez a konkrét állítás és annak fordítottja egyaránt igaz, de ez egyáltalán nem mindig
a helyzet.
például a következő két állítás egymás beszélgetése:
‘ a 4 minden többszöröse páros szám.’
‘minden páros szám 4 többszöröse.’
és itt az első állítás igaz, de a második hamis.
7. gyakorlat
írja le:
a![]() igaz geometriai állítás, amelynek fordítottja szintén igaz,
igaz geometriai állítás, amelynek fordítottja szintén igaz,
b![]() hamis geometriai állítás, amelynek fordítottja igaz,
hamis geometriai állítás, amelynek fordítottja igaz,
c![]() hamis geometriai állítás, amelynek fordítottja szintén hamis.
hamis geometriai állítás, amelynek fordítottja szintén hamis.
a párhuzamos vonalak fordított tételei
láttuk, hogy a párhuzamos vonalakból kialakított megfelelő szögek egyenlőek. A fordított állítást a következőképpen írhatjuk le.
állítás: ha a vonalak párhuzamosak, akkor a megfelelő szögek egyenlőek.
beszélgetés: Ha a megfelelő szögek egyenlőek, akkor a vonalak párhuzamosak.
a fordított állítás is igaz, és gyakran használják annak bizonyítására, hogy két vonal párhuzamos. Ugyanez igaz az alternatív és a belső szögekre is.
állítás: ha a vonalak párhuzamosak, akkor az alternatív szögek egyenlőek.
Converse: ha az alternatív szögek egyenlőek, akkor a vonalak párhuzamosak.
állítás: ha a vonalak párhuzamosak, akkor a belső belső szögek kiegészítőek.
beszélgetés: Ha a belső belső szögek kiegészítőek, akkor a vonalak párhuzamosak.
így minden diagramban az AB és a CD vonalak párhuzamosak.

gyakorlat 8
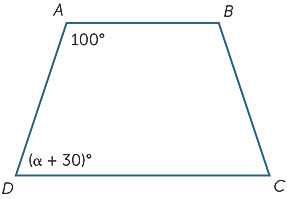 melyik értéke teszi az AB-t párhuzamossá a CD-vel?
melyik értéke teszi az AB-t párhuzamossá a CD-vel?
a három beszélgetés bizonyítékai
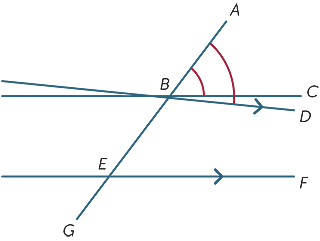 feltételezzük, hogy a keresztirányban kialakított megfelelő szögek egyenlőek, és megmutatjuk, hogy a vonalak párhuzamosak.
feltételezzük, hogy a keresztirányban kialakított megfelelő szögek egyenlőek, és megmutatjuk, hogy a vonalak párhuzamosak.
az ábrán feltételezzük, hogy ![]() ABC =
ABC = ![]() BEF.
BEF.
ha a BC és az EF nem párhuzamos, akkor rajzoljon
BD párhuzamot az EF-fel.
mivel a BD és az EF párhuzamosak ![]() ABD =
ABD = ![]() BEF és így
BEF és így ![]() ABC =
ABC = ![]() ABD, ami nyilvánvalóan lehetetlen, hacsak a BC és a BD vonalak nem azonosak. Ezért a BC és az EF vonalak párhuzamosak.
ABD, ami nyilvánvalóan lehetetlen, hacsak a BC és a BD vonalak nem azonosak. Ezért a BC és az EF vonalak párhuzamosak.
a többi bizonyíték is hasonló módon történik.
9.gyakorlat
adjon bizonyítékot a második converse tételre (alternatív szögek).
háromszög Szögösszege
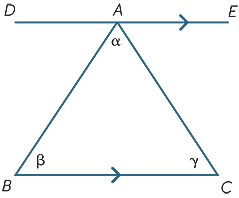 az előző szakasz eredményei felhasználhatók a geometria egyik legfontosabb tényének levezetésére − egy háromszög szögösszege 180^ .
az előző szakasz eredményei felhasználhatók a geometria egyik legfontosabb tényének levezetésére − egy háromszög szögösszege 180^ .
az ABC háromszöggel kezdjük, amelynek szögei az alábbiak szerint vannak. Rajzolja meg a DAE vonalat BC-vel párhuzamosan. Akkor,
![]() DAB = (váltakozó szögek, időszámításunk előtt / / DE)
DAB = (váltakozó szögek, időszámításunk előtt / / DE)
![]() EAC = (váltakozó szögek, időszámításunk előtt| / DE)
EAC = (váltakozó szögek, időszámításunk előtt| / DE)
+ + + = 180 (egyenes szög).
így bebizonyítottuk, hogy a tétel
a háromszög szögeinek összege 180^.
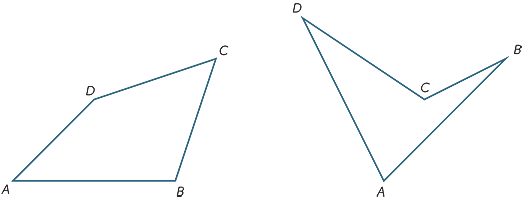
a négyszög egy négy oldal által határolt sík alak.
10.Gyakorlat
az ABCD négyszög két háromszögre osztásával keresse meg a szögek összegét.
Links forward
az anyag ebben a modulban kezdte elhelyezni geometria ésszerűen szisztematikus alapja gondosan meghatározott tárgyak, axiómák, amelyeket fel kell tételezni, és tételek, hogy már bizonyított. Ennek alapján kidolgozhatunk egy szisztematikus beszámolót a sík geometriájáról, amely magában foglalja:
- Pitagorasz-tétel
- egybevágó és egybevágó háromszögek
- hasonlóság és hasonló háromszögek
- egyenlő szárú és egyenlő oldalú háromszögek
- speciális négyszögek, beleértve a négyzeteket, téglalapokat, paralelogrammákat, rombuszokat és trapézokat
- a körök geometriája.
a síkgeometria a 7-10. évek sok más területén is alapvető fontosságú lesz matematika:
- transzformációk
- háromdimenziós geometria
- területek és kötetek
- trigonometria
- koordináta geometria
- a körök és parabolák grafikonjai.
az érintők és területek eszméi a 11-12.
történelem és alkalmazás
történelem
az egyiptomi piramisok és hatalmas templomok hihetetlen építményei azt mutatják, hogy az egyiptomiaknak nagyon jó ismeretekkel és ismeretekkel kellett rendelkezniük az alapvető geometriáról, legalábbis gyakorlati szinten. Másrészt nincs bizonyíték arra, hogy ezt a tudást bármilyen formális módon szisztematizálták volna. Ezt az ókori görögök hagyták. Nincs részletes ismeretünk erről a rendszerezésről, kivéve azt az állítást, hogy Thales (kb. E. 624-kb. E. 546) adta meg a geometriai tények első bizonyítékait, amelyek a deduktív geometria kezdetét jelentették. A Pitagorasz Iskola folytatta ezt a munkát, és Platón (428 BC -348 BC) egyértelműen támaszkodva a munka a korábbi matematikusok, amikor megemlíti geometriai tényeket írásaiban. A geometriai párbeszéd munkájában a Meno, amelyben Szókratész egy rabszolgafiút kap, hogy logikai levonások sorozatával geometriai tételhez jusson, érdemes elolvasni. Ha a geometria eredete nem egyértelmű, akkor a végtermék nem az. Euclid (323-283 BC), Alexandriában írt, figyelemre méltó munkát készített az elemek néven, amely több mint 2000 éve a geometria szokásos tankönyve maradt. Ebben a munkában Euklidész számos meghatározást (például pontokat és vonalakat), posztulátumokat és közös fogalmakat határoz meg. (Manapság ezeket axiómáknak nevezzük.) Ezekből, ő logikusan kifejlesztett, egy nagyon gondosan kiválasztott sorrendben, sok tétel, amely általában nevezik euklideszi geometria. Számos más geometriai eredmény létezik, például Pappus tétele, amelyeket Euklidész után fedeztek fel, de ezekre általában nem terjed ki a középiskola.
Euklidész öt posztulátumának egyike nem volt olyan nyilvánvalóan igaz,mint a többiek. Az egyik változata, az úgynevezett Playfair axiómája kimondja, hogy: Adott egy sor  és egy pont P, nem
és egy pont P, nem  , van egy és csak egy vonal párhuzamos
, van egy és csak egy vonal párhuzamos  áthaladó P. a 19. században, számos matematikus feltette a kérdést, ‘Mi történik, ha tagadjuk ezt a posztulátumot? Ez úgy történik, hogy feltételezzük, hogy vagy nincs ilyen párhuzamos vonal, vagy azt mondjuk, hogy egynél több ilyen vonal van. Ez a nem euklideszi geometriák kialakulásához vezetett, amelyek közül az egyik kiderült, hogy az univerzum egyik jó modelljét nyújtja.
áthaladó P. a 19. században, számos matematikus feltette a kérdést, ‘Mi történik, ha tagadjuk ezt a posztulátumot? Ez úgy történik, hogy feltételezzük, hogy vagy nincs ilyen párhuzamos vonal, vagy azt mondjuk, hogy egynél több ilyen vonal van. Ez a nem euklideszi geometriák kialakulásához vezetett, amelyek közül az egyik kiderült, hogy az univerzum egyik jó modelljét nyújtja.
Applications
egy nagyon is valós értelemben, geometria és geometriai intuíció alkotják az alapjait minden
matematika − geometria vezet koordináta geometria ami kalkulus és
minden sok alkalmazás − és így elengedhetetlen a tantervben.
gyakorlatiasabb szinten az építők, földmérők, mérnökök és építészek évszázadok óta használják a geometriát és a geometriai ötleteket. A közelmúltban a számítógépek fejlesztésével a grafikusok és a webes tervezők csatlakoztak ehhez a csoporthoz, akiknek szükségük van a geometriára és használják a munkájukat. Arra a kérdésre, hogy a közelmúltban mennyire hasznos a geometria, Jim Kelly, – mondta egy alkalmazott tudós:… a geometria a tervezés, a rajzolás és a számítógépes modellezés fontos része. Azt is gyakran használják … fizika és más fizikai tudomány tanfolyamok részeként hatásainak megértése terhelések struktúrák és kiegyensúlyozó pontok (súlypontok) kompozit szilárd anyagok. A kémiában a molekula geometriájának megértése összefügg az anyagok tulajdonságainak megértésével. Sokkal több példa létezik. (az Ask A Scientist honlapján.)
a matematika története: Bevezetés, 3. kiadás, Victor J. Katz, Addison-Wesley, (2008)
a matematika története, D. E. Smith, Dover publications New York, (1958)
válaszok a gyakorlatokra
gyakorlat 1
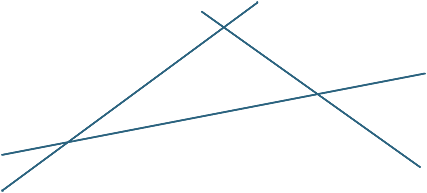
GYAKORLAT 2
A pontok egy egyenesre esnek
GYAKORLAT 3
60°
GYAKORLAT 4
![]() DBA = 102° (megfelelő szögek, AB||CD)
DBA = 102° (megfelelő szögek, AB||CD)
![]() BAC = 78° (co-belső szögek, AC||BD)
BAC = 78° (co-belső szögek, AC||BD)
GYAKORLAT 5
α = 65°![]() (megfelelő szögek, AC||BM)
(megfelelő szögek, AC||BM)
β = 80°![]() (alternatív szögek, AC||BM)
(alternatív szögek, AC||BM)
γ + β = 115°![]() (co-belső szögek, AC||BM)
(co-belső szögek, AC||BM)
Ezért γ = 35°
(Ez a szerkezet egy bizonyíték az eredménye, hogy a szög összege egy háromszögben 180°)
6.gyakorlat
oni = 60 6751>
7. gyakorlat
a ![]() négyszög minden belső szögével a derékszög egy téglalap.
négyszög minden belső szögével a derékszög egy téglalap.
Converse: egy téglalap minden belső szöge derékszög.
b![]() a téglalap egy négyzet
a téglalap egy négyzet
Converse: a négyzet egy téglalap
c![]() a szög összege a belső szögek egy háromszög 200 ons
a szög összege a belső szögek egy háromszög 200 ons
Converse: a sokszög, amely az összeg a belső szög 200 Ft egy háromszög.
8.gyakorlat
60 6751>
9. gyakorlat
ugyanarra az ábrára utalunk.
helyezzen egy H pontot az EF vonalra az E-től balra.
![]() CBE =
CBE = ![]() BEH
BEH
ha a BC és az EF nem párhuzamosak, akkor húzzon BD párhuzamot az EF-fel.
mivel a BD és az EF párhuzamosak, ![]() EBD=
EBD= ![]() BEH, ami nyilvánvalóan lehetetlen, hacsak a BC és a BD vonalak nem azonosak.
BEH, ami nyilvánvalóan lehetetlen, hacsak a BC és a BD vonalak nem azonosak.
ezért a BC és az EF vonalak párhuzamosak.
gyakorlat 10
360°
az Improving Mathematics Education in Schools (TIMES) projektet 2009-2011-ben az ausztrál kormány oktatási, foglalkoztatási és munkahelyi kapcsolatok Minisztériuma finanszírozta.
az itt kifejtett nézetek a szerző nézetei, és nem feltétlenül tükrözik az ausztrál kormány oktatási, foglalkoztatási és munkahelyi kapcsolatok Minisztériumának nézeteit.
a melbourne-i egyetem nevében a nemzetközi Kiválósági Központ oktatási matematika (ICE-EM), az oktatási osztály az Ausztrál Matematikai Tudományok Intézet (AMSI), 2010 (kivéve, ha másként jelezzük). Ez a munka a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported Licenc alatt engedélyezett.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()