terminológia:
- IDS = áram a lefolyótól a forrásig vagy lefolyó-forrás áram
- VDS = lefolyó forrás feszültség
- L = a csatorna hossza
ideális esetben a telítettségi tartományban az IDS függetlenné válik a VDS-től, azaz a telítettségi régióban a csatorna le van szorítva a lefolyó végén, és a VDS további növekedése nincs hatással a csatorna alakjára.
de a gyakorlatban a VDS növekedése befolyásolja a csatornát. A telítettségi régióban, amikor a VDS növekszik, a csatorna csípési pontja kissé elmozdul a lefolyótól, a forrás felé, amikor a lefolyó elektronmező “visszatolja”. A fordított torzítás kimerülési régiója kiszélesedik, a tényleges csatorna hossza pedig a VDS növekedése miatt csökken.
így a csatorna már nem “érinti” a lefolyót, és aszimmetrikus alakot kap, amely vékonyabb a lefolyó végén. Ezt a jelenséget csatornahossz-modulációnak nevezik.
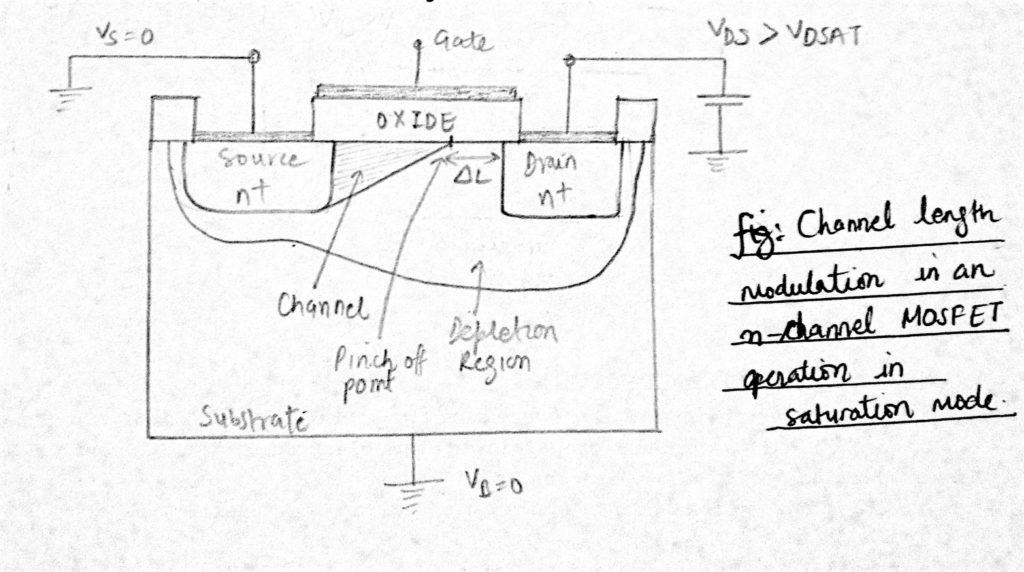
nagy készülékeknél ez a hatás elhanyagolható, de a rövidebb eszközöknél fontos lesz az l / l. A csatornahossz-moduláció miatt a telítettségi régióban az IDS a VDS növekedésével, valamint az L csatorna hosszának csökkenésével is növekszik.
a feszültség-áram görbe már nem lapos ebben a régióban.
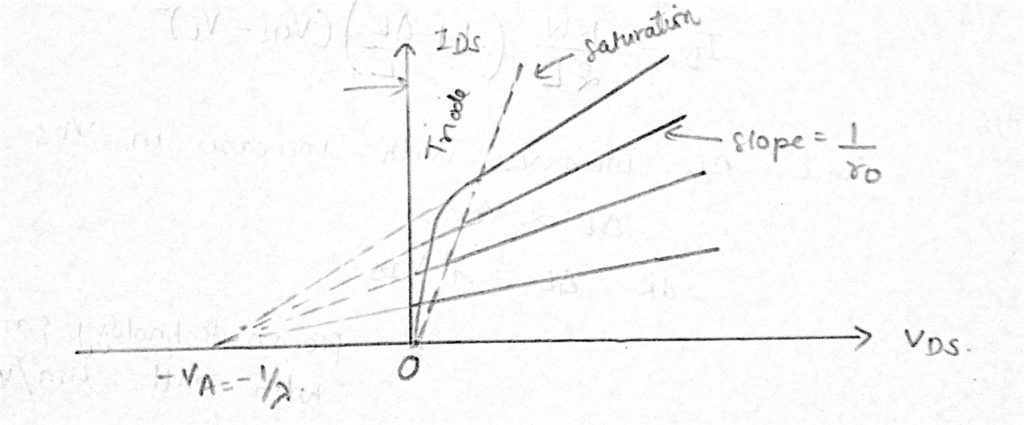
a csatornahossz-modulációval rendelkező lefolyóáramot az adja meg:
levezetés:
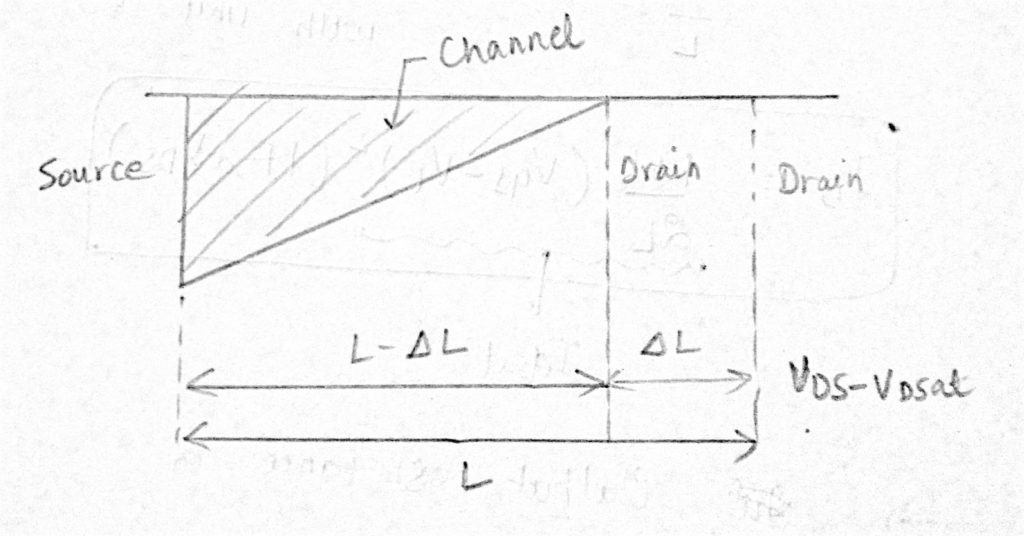
annak érdekében, hogy figyelembe vegyük az ID függését a VDS-től a telítettségi régióban, cserélje ki L – val L – 6-L. tudjuk, hogy a telítettségi régióban a forrásáramot (IDS = ID) a:
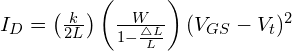
feltételezve 
mivel a VDS növekedésével az L növekszik
vagy
ahol 
= folyamattechnológiai paraméter egységgel (egységnyi) M / V.
ezért,
ahol,
= folyamat technológiai paraméter v egységgel-1
