Assessment | Biopszichológia | összehasonlító |kognitív | fejlődési | nyelv | egyéni különbségek |személyiség | filozófia | társadalmi |
módszerek | statisztika |klinikai | oktatási | ipari |szakmai tételek |Világpszichológia |
statisztika:tudományos módszer · kutatási módszerek · kísérleti tervezés · egyetemi statisztikai tanfolyamok · statisztikai tesztek · játékelmélet · döntéselmélet
kérjük, segítsen javítani ezt az oldalt magad, ha tudsz..
a klaszterelemzés vagy a klaszterezés a statisztikai adatok elemzésének általános technikája, amelyet számos területen használnak, beleértve a gépi tanulást, az adatbányászatot, a mintafelismerést, a képelemzést és a bioinformatikát. A fürtözés a hasonló objektumok különböző csoportokba történő besorolása, vagy pontosabban az adathalmaz részhalmazokra (klaszterekre) történő particionálása, így az egyes részhalmazok adatai (ideális esetben) megosztanak valamilyen közös tulajdonságot – gyakran a közelséget valamilyen meghatározott távolságmérés szerint.
az adatcsoportosítás (vagy csak klaszterezés) kifejezés mellett számos hasonló jelentéssel bíró kifejezés létezik, beleértve a klaszteranalízist, az automatikus osztályozást, a numerikus taxonómiát, a botryológiát és a tipológiai elemzést.
- a klaszterezés típusai
- hierarchikus csoportosítás
- Távolságmérés
- klaszterek létrehozása
- Agglomeratív hierarchikus fürtözés
- partíciós fürtözés
- k-közép és származékai
- K-Közép klaszterezés
- QT Clust algoritmus
- Fuzzy C-azt jelenti, klaszterezés
- Könyökkritérium
- spektrális csoportosítás
- Alkalmazások
- Biológia
- marketingkutatás
- egyéb alkalmazások
- adatcsoportok összehasonlítása
- Lásd még
- bibliográfia
- szoftver implementációk
- ingyenes
a klaszterezés típusai
az Adatcsoportosítási algoritmusok hierarchikusak vagy particionálisak lehetnek. A hierarchikus algoritmusok egymást követő klasztereket találnak korábban létrehozott klaszterek segítségével, míg a partíciós algoritmusok egyszerre határozzák meg az összes klasztert. A hierarchikus algoritmusok lehetnek agglomeratívak (alulról felfelé) vagy osztóak (felülről lefelé). Az agglomeratív algoritmusok minden egyes elemet külön klaszterként kezdenek, majd egymás után nagyobb klaszterekbe egyesítik őket. Az osztó algoritmusok az egész halmazzal kezdődnek, majd egymás után kisebb klaszterekre osztják.
hierarchikus csoportosítás
Távolságmérés
a hierarchikus csoportosítás kulcsfontosságú lépése a távolságmérés kiválasztása. Egy egyszerű mérték manhattan távolság, egyenlő az egyes változók abszolút távolságának összegével. A név abból a tényből származik, hogy kétváltozós esetben a változókat egy rácsra lehet ábrázolni, amely összehasonlítható a városi utcákkal, és a két pont közötti távolság az a blokkszám, amelyet egy személy megtenne.
egy általánosabb mérték az euklideszi távolság, amelyet úgy számítunk ki, hogy megtaláljuk az egyes változók közötti távolság négyzetét, összeadjuk a négyzeteket, és megtaláljuk az összeg négyzetgyökét. Kétváltozós esetben a távolság analóg a hipotenusz hosszának háromszögben történő megtalálásával; vagyis ez a távolság ” ahogy a varjú repül.”Az Egészségpszichológiai kutatások klaszterelemzésének áttekintése megállapította, hogy az adott kutatási területen publikált tanulmányokban a leggyakoribb távolságmérő az euklideszi távolság vagy a négyzet euklideszi távolság.
klaszterek létrehozása
adott távolságmérés esetén az elemek kombinálhatók. A hierarchikus csoportosítás a klaszterek hierarchiáját építi fel (agglomeratív), vagy felbomlik (megosztó). Ennek a hierarchiának a hagyományos ábrázolása a fa adatstruktúra (úgynevezett a dendrogram), egyik végén egyedi elemekkel, a másikban pedig egyetlen klaszterrel, minden elemmel. Az agglomeratív algoritmusok a fa tetején kezdődnek, míg az osztó algoritmusok az alján kezdődnek. (Az ábrán a nyilak agglomeratív csoportosulást jeleznek.)
a fa egy adott magasságban történő vágása egy kiválasztott pontosságú fürtözést eredményez. A következő példában a második sor utáni vágás {a} {b c} {d E} {f} fürtöket eredményez. A harmadik sor utáni vágás {a} {b c} {d E f} fürtöket eredményez, ami durvább klaszterezés, kevesebb nagyobb klaszterrel.
Agglomeratív hierarchikus fürtözés
tegyük fel például, hogy ezeket az adatokat csoportosítani kell. Ahol euklideszi távolság a távolság metrikus.
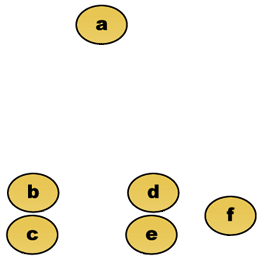
nyers adatok
a hierarchikus klaszterező dendrogram önmagában lenne:
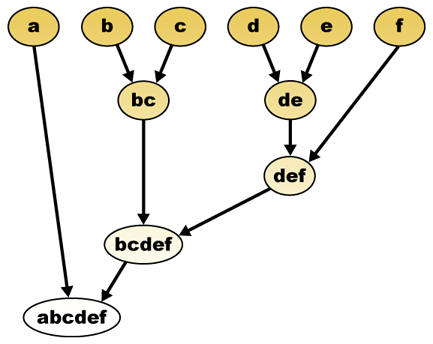
hagyományos képviselet
ez a módszer a hierarchiát az egyes elemekből építi fel a klaszterek fokozatos egyesítésével. Ismét hat elemünk van {a} {b} {c} {d} {e} és {f}. Az első lépés annak meghatározása, hogy mely elemeket kell egyesíteni egy fürtben. Általában a két legközelebbi elemet akarjuk venni, ezért meg kell határoznunk a távolságot 
tegyük fel, hogy egyesítettük a két legközelebbi B és c elemet, most a következő klaszterekkel rendelkezünk {a}, {b, c}, {d}, {e} és {f}, és tovább akarjuk egyesíteni őket. De ehhez meg kell vennünk az {a} és {b c} közötti távolságot, és ezért meg kell határoznunk a két klaszter közötti távolságot. Két klaszter 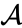
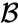
- az egyes klaszterek elemei közötti maximális távolság (más néven teljes összekapcsolási klaszterezés):
- az egyes klaszterek elemei közötti minimális távolság (más néven egykötéses klaszterezés):
- az egyes klaszterek elemei közötti átlagos távolság (más néven átlagos összekapcsolási klaszterezés):
- az összes klaszteren belüli variancia összege
- az egyesítendő klaszter varianciájának növekedése (Ward kritériuma)
- annak valószínűsége, hogy a jelölt klaszterek ugyanabból az eloszlási függvényből származnak (V-kapcsolat)
minden egyes agglomeráció nagyobb távolságban fordul elő a klaszterek között, mint az előző agglomeráció, és dönthet úgy, hogy abbahagyja a klaszterezést, ha a klaszterek túl messze vannak egymástól ahhoz, hogy összeolvadjanak (távolságkritérium), vagy ha kellően kis számú klaszter van (számkritérium).
partíciós fürtözés
k-közép és származékai
K-Közép klaszterezés
a K-Közép algoritmus minden pontot hozzárendel ahhoz a klaszterhez, amelynek középpontja (más néven centroid) a legközelebbi. A középpont a fürt összes pontjának átlaga-Vagyis koordinátái az egyes dimenziók számtani átlaga külön-külön a fürt összes pontján.
példa: Az adathalmaznak három dimenziója van, a fürtnek pedig két pontja van: X = (x1, x2, x3) és Y = (y1, y2, y3). Ekkor a Z centroid Z = (z1, z2, z3) lesz, ahol z1 = (x1 + y1)/2 és z2 = (x2 + y2)/2 és z3 = (x3 + y3)/2.
az algoritmus nagyjából (J. MacQueen, 1967):
- véletlenszerűen generál k klasztereket és meghatározza a klaszter központokat, vagy közvetlenül generál k magpontokat klaszter központokként.
- rendeljen minden pontot a legközelebbi fürtközponthoz.
- számolja újra az új klaszterközpontokat.
- ismételje meg, amíg valamelyik konvergenciakritérium teljesül (általában a hozzárendelés nem változott).
az algoritmus fő előnye az egyszerűsége és sebessége, amely lehetővé teszi, hogy nagy adatkészleteken fusson. Hátránya, hogy nem minden futásnál ugyanazt az eredményt adja, mivel a kapott klaszterek a kezdeti véletlenszerű hozzárendelésektől függenek. Maximalizálja a klaszterek közötti (vagy minimalizálja a klaszteren belüli) varianciát, de nem biztosítja, hogy az eredmény globális minimális varianciával rendelkezzen.
QT Clust algoritmus
QT (minőségi küszöb) klaszterezés (Heyer et al, 1999) egy alternatív módszer az adatok particionálására, amelyet géncsoportosításra találtak ki. Nagyobb számítási teljesítményt igényel, mint a k-means, de nem igényli a klaszterek számának a priori megadását, és mindig ugyanazt az eredményt adja vissza, ha többször fut.
az algoritmus:
- a felhasználó kiválasztja a klaszterek maximális átmérőjét.
- hozzon létre egy jelölt klasztert minden ponthoz úgy, hogy belefoglalja a legközelebbi pontot, a legközelebbi legközelebb stb., amíg a klaszter átmérője meghaladja a küszöböt.
- mentse el a legtöbb pontot tartalmazó jelölt fürtöt első valódi fürtként, és távolítsa el a fürt összes pontját a további megfontolásból.
- Rekurzálja a csökkentett pontkészletet.
egy pont és egy pontcsoport közötti távolságot teljes összekapcsolással kell kiszámítani, azaz. a maximális távolság a ponttól a csoport bármely tagjáig (lásd az “Agglomeratív hierarchikus klaszterezés” részt a klaszterek közötti távolságról).
Fuzzy C-azt jelenti, klaszterezés
fuzzy fürtözés, minden pont bizonyos fokú tartozó klaszterek, mint a fuzzy logika, ahelyett tartozó teljesen csak egy klaszter. Így a klaszter szélén lévő pontok kisebb mértékben lehetnek a klaszterben, mint a klaszter közepén lévő pontok. Minden X pontra van egy együtthatónk, amely megadja a K-edik klaszterben való lét fokát 

fuzzy C-átlag esetén a klaszter centroidja az összes pont átlaga, súlyozva a klaszterhez való tartozás mértékével:
az összetartozás mértéke a klaszter távolságának inverzével függ össze
ezután az együtthatókat egy 
M egyenlő 2 – vel, ez egyenértékű az együttható lineárisan történő normalizálásával, hogy összegük 1 legyen. Ha m közel van az 1-hez, akkor a ponthoz legközelebb eső klaszterközpont sokkal nagyobb súlyt kap, mint a többiek, és az algoritmus hasonló a k-átlaghoz.
a fuzzy c-means algoritmus nagyon hasonlít a k-means algoritmushoz:
- Válasszon több klasztert.
- véletlenszerűen rendeljen minden egyes pont együtthatóhoz a klaszterekben való tartózkodáshoz.
- addig ismételjük, amíg az algoritmus konvergál (vagyis az együtthatók változása két iteráció között nem nagyobb, mint
, a megadott érzékenységi küszöb) :
- Számítsa ki az egyes klaszterek centroidját a fenti képlet segítségével.
- minden ponthoz számítsa ki a klaszterekben való együtthatóit a fenti képlet segítségével.
az algoritmus minimalizálja a klaszteren belüli varianciát is, de ugyanazokkal a problémákkal rendelkezik, mint a k-means, a minimum helyi minimum, az eredmények pedig a súlyok kezdeti megválasztásától függenek.
Könyökkritérium
a könyökkritérium általános szabály annak meghatározására, hogy milyen számú klasztert kell választani, például k-közép és agglomeratív hierarchikus klaszterezés esetén.
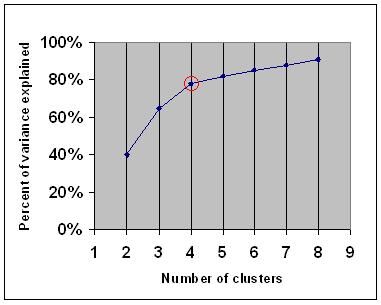
a könyökkritérium azt mondja, hogy több fürtöt kell választania, hogy egy másik fürt hozzáadása ne adjon elegendő információt. Pontosabban, ha a klaszterek által magyarázott variancia százalékát ábrázolja a klaszterek számával, akkor az első klaszterek sok információt adnak hozzá (sok varianciát magyaráznak), de egy bizonyos ponton a marginális nyereség csökken, szöget adva a grafikonban (a könyök).
a következő grafikonon a könyök piros körrel van jelölve. Ezért a kiválasztott klaszterek számának 4-nek kell lennie.
spektrális csoportosítás
adatpontok halmaza alapján a hasonlósági mátrix meghatározható úgy, mint egy mátrix 


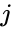
az egyik ilyen technika A Shi-Malik algoritmus, amelyet általában a kép szegmentálásához használnak. Két csoportra osztja a pontokat 


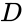
ez a particionálás többféle módon is elvégezhető, például úgy, hogy a 



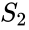
egy kapcsolódó algoritmus a Meila-Shi algoritmus, amely a 
Alkalmazások
Biológia
a biológiában a klaszterezés számos alkalmazással rendelkezik a számítási biológia és a bioinformatika területén, amelyek közül kettő:
- a transzkriptomikában a klaszterezést a kapcsolódó expressziós mintákkal rendelkező géncsoportok felépítésére használják. Az ilyen csoportok gyakran funkcionálisan rokon fehérjéket tartalmaznak, például enzimeket egy adott útvonalhoz, vagy géneket, amelyek társszabályozottak. Nagy áteresztőképességű kísérletek expresszált szekvenciacímkék (est) vagy DNS mikroarray segítségével hatékony eszköz lehet Genom annotáció, a genomika általános aspektusa.
- a szekvenciaelemzésben a klaszterezést a homológ szekvenciák géncsaládokba történő csoportosítására használják. Ez egy nagyon fontos fogalom a bioinformatikában és általában az evolúciós biológiában. Lásd evolúció gén duplikációval.
marketingkutatás
a Klaszterelemzést széles körben használják a piackutatásban, amikor felmérések és tesztpanelek többváltozós adataival dolgoznak. A piackutatók klaszterelemzést alkalmaznak a fogyasztók általános populációjának piaci szegmensekre történő felosztására és a fogyasztók/potenciális vásárlók különböző csoportjai közötti kapcsolatok jobb megértésére.
- a piac szegmentálása és a célpiacok meghatározása
- Termékpozicionálás
- új termékfejlesztés
- Tesztpiacok kiválasztása (lásd : Kísérleti technikák)
egyéb alkalmazások
Social network analysis: A tanulmány a szociális hálózatok, klaszterezés lehet használni felismerni közösségek nagy embercsoportok.
Képszegmentálás: a klaszterezés felhasználható a digitális kép elkülönített régiókra történő felosztására határfelismerés vagy objektumfelismerés céljából.
adatbányászat: sok adatbányászati alkalmazás magában foglalja az adatelemek particionálását kapcsolódó részhalmazokba; a fent tárgyalt marketing alkalmazások néhány példát képviselnek. Egy másik gyakori alkalmazás a dokumentumok, például a World Wide Web oldalak műfajokra osztása.
adatcsoportok összehasonlítása
számos javaslat született két klaszter hasonlóságának mérésére. Egy ilyen intézkedés felhasználható annak összehasonlítására, hogy a különböző adatcsoportosítási algoritmusok milyen jól teljesítenek egy adathalmazon. Ezen intézkedések közül sok a matching matrix (más néven confusion matrix), például a Rand intézkedés és a Fowlkes-Mallows Bk intézkedések.
- Jain, Murty és Flynn: Data Clustering: a Review, ACM Comp. Surv., 1999. Elérhető itt.
- a hierarchikus, K-means és fuzzy c-means további bemutatását lásd a fürtözés bevezetőjében. Van egy magyarázat a Gaussok keverékéről is.
- David Dowe, Keverékmodellezés oldal – Egyéb klaszterezés és keverékmodell linkek.
- a tutorial on clustering
- az On-line tankönyv: információelmélet, következtetés, és tanulási algoritmusok, David J. C. MacKay fejezeteket tartalmaz K-means klaszterezés, puha k-means klaszterezés, és levezetések, beleértve az e-m algoritmus és a variációs nézet az e-m algoritmus.
Lásd még
- k-eszközök
- mesterséges neurális hálózat (ANN)
- önszerveződő térkép
- elvárások maximalizálása (EM)
bibliográfia
- Clatworthy, J., Buick, D., Hankins, M., Weinman, J., & Horne, R. (2005). A klaszterelemzés használata és jelentése az egészségpszichológiában: áttekintés. Brit Egészségpszichológiai folyóirat 10: 329-358.
- Romesburg, H. Clarles, Cluster Analysis for Researchers, 2004, 340 pp. ISBN 1411606175 vagy kiadó, az 1990-es kiadás újranyomtatása, amelyet a Krieger Pub adott ki. Sz… Japán nyelvű fordítás érhető el az Uchida Rokakuho Publishing Co., Kft., Tokió, Japán.
- Heyer, L. J., Kruglyak, S. és Yooseph, S., Exploring Expression Data:Identification and Analysis of Coexpressed Genes, Genome Research 9: 1106-1115.
- az On-line tankönyv: információelmélet, következtetés és tanulási algoritmusok, David J. C. MacKay fejezeteket tartalmaz a k-means klaszterezésről, a puha k-means klaszterezésről és a levezetésekről, beleértve az E-M algoritmust és az E-M algoritmus variációs nézetét.
színképcsoportosításhoz :
- Jianbo Shi és Jitendra Malik, “Normalized Cuts and Image Szegmentation”, IEEE tranzakciók a Mintaelemzésről és a gépi intelligenciáról, 22(8), 888-905, 2000.augusztus. Elérhető Jitendra Malik honlapján
- Marina Meila and Jianbo Shi, “Learning Szegmentation with Random Walk”, neurális információfeldolgozó rendszerek, NIPS, 2001. Elérhető a jianbo Shi honlapjáról
a klaszterek számának becsléséhez:
- Can, F., Ozkarahan, E. A. (1990) ” a szöveges adatbázisok fedési együtthatón alapuló fürtözési módszertanának koncepciói és hatékonysága.”ACM tranzakciók adatbázis rendszerek. 15 (4) 483-517.
szoftver implementációk
ingyenes
- a flexclust csomag R
- YALE (még egy tanulási környezet): ingyenes nyílt forráskódú szoftver a tudásfeltáráshoz és az adatbányászathoz, beleértve egy plugint is a fürtözéshez
- néhány Matlab forrásfájl a fürtözéshez itt
- compact-összehasonlító csomag klaszter értékelés (szintén Matlab)
- mixmod : Modell Alapú Klaszter És Diszkrimináns Elemzés. Kód C++ – ban, interfész a Matlab és a Scilab
- LingPipe Clustering Tutorial Tutorial a teljes és egy linkes klaszterezéshez a lingpipe használatával, egy Java szöveges adatbányászati csomag, amelyet a forrással osztanak szét.
- Weka : a Weka eszközöket tartalmaz az adatok előfeldolgozásához, osztályozásához, regressziójához, fürtözéséhez, asszociációs szabályokhoz és vizualizációhoz. Kiválóan alkalmas új gépi tanulási rendszerek kidolgozására is.