Noam Chomosky szerint a nyelvtanoknak négy típusa van: 0. Típus, 1.Típus, 2. típus és 3. Típus. Az alábbi táblázat bemutatja, hogyan különböznek egymástól−
| nyelvtan Típus | nyelvtan elfogadott | nyelv elfogadott | automata |
|---|---|---|---|
| 0 Típus | korlátlan nyelvtan | rekurzívan felsorolható nyelv | Turing-gép |
| 1. típus | kontextus – érzékeny nyelvtan | kontextus-érzékeny nyelv | lineáris határolt automata |
| 2. típus | Kontextusmentes nyelvtan | Kontextusmentes nyelv | Pushdown automata |
| 3. Típus | rendszeres nyelvtan | rendszeres nyelv | véges állapotú automata |
vessen egy pillantást a következő ábrára. Ez azt mutatja, a hatálya minden típusú nyelvtan –
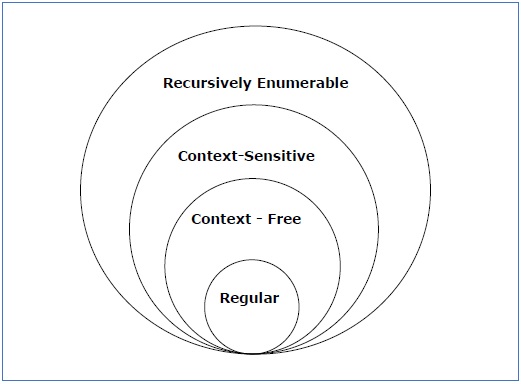
Type – 3 nyelvtan
Type-3 nyelvtanok generálni szabályos nyelvek. A 3. típusú nyelvtanoknak egyetlen nem terminállal kell rendelkezniük a bal oldalon, a jobb oldalon pedig egyetlen terminállal vagy egyetlen terminállal, amelyet egyetlen nem terminál követ.
a produkciók kell lennie a következő formában: x (a) A vagy X (a) a
ahol X, Y (nem vég) N (7526>
és a (A) t (a)
az S (A) szabály megengedett, ha s nem jelenik meg a szabály jobb oldalán.
példa
X → ε X → a | aYY → b
2.típusú nyelvtan
2. típusú nyelvtanok kontextus nélküli nyelveket generálnak.
a produkciók a következők: a (7526>
ahol A (nem terminál)
és a (T)* (sorkapcsok és nem terminálok sora).
ezeket a nyelvtanok által generált nyelveket egy nem determinisztikus pushdown automata ismeri fel.
példa
S → X a X → a X → aX X → abc X → ε
1.típusú nyelvtan
1. típusú nyelvtanok környezetfüggő nyelveket generálnak. A produkciók kell formájában
α β → α γ β
, ahol A ∈ N (terminálon)
az α, β, γ ∈ (T ∪ N)* (Húrok terminálok, valamint a nem-terminálok)
A húrok α, illetve β lehet üres, de γ biztosan nem üres.
az S szabály megengedett, ha s nem jelenik meg egyetlen szabály jobb oldalán sem. Az ezen nyelvtanok által generált nyelveket egy lineáris határolt automata ismeri fel.
példa
AB → AbBc A → bcA B → b
0 típusú nyelvtan
0 típusú nyelvtanok rekurzívan felsorolható nyelveket generálnak. A produkcióknak nincsenek korlátozásai. Ezek bármilyen fázisszerkezeti nyelvtan, beleértve az összes formális nyelvtanot.
generálják azokat a nyelveket, amelyeket egy Turing-gép felismer.
A produkcióban formájában α → β, ahol α egy string terminálok, valamint a halálos betegség nélkülieknek legalább egy terminálon pedig α nem lehet null. a végpontok és a nem terminálok sorozata.
Példa
S → ACaB Bc → acB CB → DB aD → Db