4.2 A lineáris regressziós modell együtthatóinak becslése / Bevezetés Az Ökonometriába R

4.2 A lineáris regressziós modell együtthatóinak becslése

a gyakorlatban a populáció regressziós egyenes metszéspontja $\beta_0$ és meredeksége $\beta_1$ nem ismert. Ezért adatokat kell felhasználnunk mindkét ismeretlen paraméter becsléséhez. A következőkben egy valós példát fogunk használni annak bemutatására, hogy ez hogyan érhető el. Szeretnénk összekapcsolni a teszt pontszámokat a kaliforniai iskolákban mért diák-tanár arányokkal. A teszt pontszám az ötödik osztályosok olvasási és matematikai pontszámainak körzeti átlaga. Az osztálylétszámot ismét a hallgatók számának osztva a tanárok számával (a diák-tanár arány). Ami az adatokat illeti, a kaliforniai iskolai adatkészlet (CASchools) egy Aer nevű R csomaggal érkezik, amely az alkalmazott ökonometria rövidítése az R-vel (Kleiber and Zeileis 2020). A csomag telepítése után telepítse.csomagok (“AER”) és a könyvtárhoz csatolva(Aer) az adatkészlet a data () függvény segítségével tölthető be.

## # install the AER package (once)## install.packages("AER")## ## # load the AER packagelibrary(AER)# load the the data set in the workspacedata(CASchools)

a csomag telepítése után további alkalmakkor is használható, ha a library () programmal hívják meg — nincs szükség az install futtatására.csomagok () újra!

érdekes tudni, hogy milyen tárgyról van szó.a class() egy objektum osztályát adja vissza. Az objektum osztályától függően egyes függvények (pl. plot() és summary()) eltérően viselkednek.

ellenőrizzük az objektum CASchools osztályát.

class(CASchools)#> "data.frame"

kiderül, hogy a CASchools osztályadatok.keret, amely kényelmes formátum a munkához, különösen a regresszióanalízis elvégzéséhez.

a head() segítségével első áttekintést kapunk adatainkról. Ez a funkció csak az adatkészlet első 6 sorát jeleníti meg, ami megakadályozza a túlzsúfolt konzol kimenetet.

nyomja meg a ctrl + L billentyűkombinációt a konzol törléséhez. Ez a parancs törli az Ön által beírt, végrehajtott vagy az R functions által a konzolra kinyomtatott kódokat. A jó hír az, hogy minden más érintetlen marad. Ön sem laza meghatározott változók stb. sem a kód története. Még mindig lehetséges a korábban végrehajtott R parancsok visszahívása a fel és le gombokkal. Ha az RStudio alkalmazásban dolgozik, nyomja meg a ctrl + Up billentyűkombinációt a billentyűzeten (CMD + Up Mac rendszeren) a korábban beírt parancsok listájának áttekintéséhez.

head(CASchools)#> district school county grades students teachers#> 1 75119 Sunol Glen Unified Alameda KK-08 195 10.90#> 2 61499 Manzanita Elementary Butte KK-08 240 11.15#> 3 61549 Thermalito Union Elementary Butte KK-08 1550 82.90#> 4 61457 Golden Feather Union Elementary Butte KK-08 243 14.00#> 5 61523 Palermo Union Elementary Butte KK-08 1335 71.50#> 6 62042 Burrel Union Elementary Fresno KK-08 137 6.40#> calworks lunch computer expenditure income english read math#> 1 0.5102 2.0408 67 6384.911 22.690001 0.000000 691.6 690.0#> 2 15.4167 47.9167 101 5099.381 9.824000 4.583333 660.5 661.9#> 3 55.0323 76.3226 169 5501.955 8.978000 30.000002 636.3 650.9#> 4 36.4754 77.0492 85 7101.831 8.978000 0.000000 651.9 643.5#> 5 33.1086 78.4270 171 5235.988 9.080333 13.857677 641.8 639.9#> 6 12.3188 86.9565 25 5580.147 10.415000 12.408759 605.7 605.4

megállapítottuk, hogy az adathalmaz rengeteg változóból áll, amelyek többsége numerikus.

Apropó: a class() és a head() alternatívája az str (), amely a ‘structure’ – ből vezethető le, és átfogó áttekintést nyújt az objektumról. Próbáld!

visszatérve a CASchools-ra, a két változó, ami érdekel minket (pl., az átlagos teszt pontszám és a diák-tanár arány) nem szerepelnek. A megadott adatokból azonban mindkettő kiszámítható. A diák-tanár arány megszerzéséhez egyszerűen elosztjuk a hallgatók számát A tanárok számával. Az átlagos teszt pontszám az olvasási teszt pontszámának számtani átlaga, valamint a matematikai teszt pontszáma. A következő kódrészlet megmutatja, hogy a két változó hogyan építhető fel vektorként, és hogyan vannak csatolva a Caschoolokhoz.

# compute STR and append it to CASchoolsCASchools$STR <- CASchools$students/CASchools$teachers # compute TestScore and append it to CASchoolsCASchools$score <- (CASchools$read + CASchools$math)/2

ha futott head (CASchools) újra meg fogjuk találni a két változó érdekes, mint további oszlopok nevű STR és pontszám (ellenőrizze ezt!).

a tankönyv 4.1.táblázata összefoglalja a teszteredmények eloszlását és a diák-tanár arányokat. Számos funkció használható hasonló eredmények elérésére, pl.,

átlag () (kiszámítja a megadott számok számtani átlagát),
sd () (kiszámítja a minta szórását),
quantile() (visszaadja a vektor a megadott minta kvantilisek az adatok).

a következő kóddarab megmutatja, hogyan lehet ezt elérni. Először is, kiszámítjuk összefoglaló statisztikák az oszlopok STR és pontszám CASchools. Annak érdekében, hogy szép kimenetet kapjunk, összegyűjtjük az intézkedéseket egy adatban.keret nevű DistributionSummary.

# compute sample averages of STR and scoreavg_STR <- mean(CASchools$STR) avg_score <- mean(CASchools$score)# compute sample standard deviations of STR and scoresd_STR <- sd(CASchools$STR) sd_score <- sd(CASchools$score)# set up a vector of percentiles and compute the quantiles quantiles <- c(0.10, 0.25, 0.4, 0.5, 0.6, 0.75, 0.9)quant_STR <- quantile(CASchools$STR, quantiles)quant_score <- quantile(CASchools$score, quantiles)# gather everything in a data.frame DistributionSummary <- data.frame(Average = c(avg_STR, avg_score), StandardDeviation = c(sd_STR, sd_score), quantile = rbind(quant_STR, quant_score))# print the summary to the consoleDistributionSummary#> Average StandardDeviation quantile.10. quantile.25. quantile.40.#> quant_STR 19.64043 1.891812 17.3486 18.58236 19.26618#> quant_score 654.15655 19.053347 630.3950 640.05000 649.06999#> quantile.50. quantile.60. quantile.75. quantile.90.#> quant_STR 19.72321 20.0783 20.87181 21.86741#> quant_score 654.45000 659.4000 666.66249 678.85999

ami a mintaadatokat illeti, a plot () – t használjuk. Ez lehetővé teszi számunkra, hogy észleljük adataink jellemzőit, például a kiugró értékeket, amelyeket a puszta számok alapján nehezebb felfedezni. Ezúttal néhány további érvet adunk a plot () hívásához.

az első argumentum a Call of plot(), pontszám ~ STR, ismét egy képlet, amely kimondja változók az y – és az x-tengely. Ezúttal azonban a két változót nem külön vektorokba menti, hanem CASchools oszlopai. Ezért R nem találná meg őket az argumentumadatok helyes megadása nélkül. az adatoknak összhangban kell lenniük az adatok nevével.keret, amelyhez a változók tartoznak, ebben az esetben CASchools. További argumentumokat használnak a telek megjelenésének megváltoztatására: míg a main hozzáad egy címet, az xlab és az ylab egyedi címkéket ad mindkét tengelyhez.

plot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)")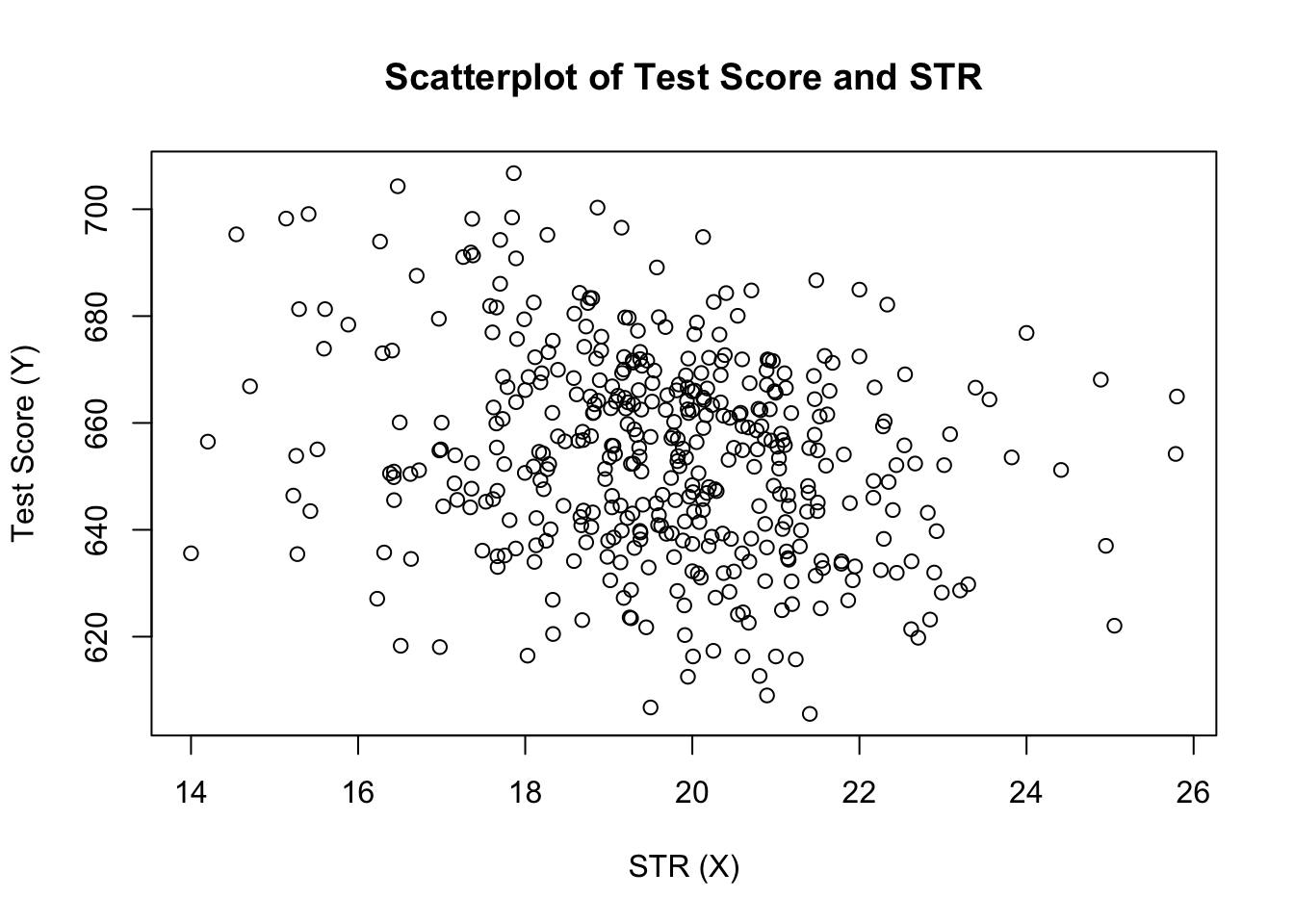

a cselekmény (a könyv 4.2.ábrája) a diák-tanár arányra és a teszt pontszámra vonatkozó összes megfigyelés szórását mutatja. Látjuk, hogy a pontok erősen szétszóródnak, és hogy a változók negatívan korrelálnak. Vagyis elvárjuk, hogy alacsonyabb teszteredményeket figyeljünk meg nagyobb osztályokban.

a cor () függvény (lásd ?cor további információkért) használható két numerikus vektor közötti korreláció kiszámításához.

cor(CASchools$STR, CASchools$score)#> -0.2263627

ahogy a scatterplot már sugallja, a korreláció negatív, de meglehetősen gyenge.

most az a feladatunk, hogy megtaláljuk az adatoknak leginkább megfelelő sort. Természetesen egyszerűen ragaszkodhatunk a grafikus ellenőrzéshez és a korrelációs elemzéshez, majd szemgolyóval kiválaszthatjuk a legjobban illeszkedő vonalat. Ez azonban meglehetősen szubjektív lenne: a különböző megfigyelők különböző regressziós vonalakat rajzolnának. Ebben a tekintetben olyan technikák érdekelnek, amelyek kevésbé önkényesek. Ezt a technikát a szokásos legkisebb négyzetek (OLS) becslésével adják meg.

a rendes legkisebb négyzetek becslő

az OLS becslő úgy választja meg a regressziós együtthatókat, hogy a becsült regressziós egyenes a lehető legközelebb legyen a megfigyelt adatpontokhoz. Itt a közelséget a $Y$ adott $X$ előrejelzésében elkövetett négyzetes hibák összegével mérjük. Legyen $b_0$ és $b_1$ néhány becslés $\beta_0$ és $\beta_1$. Ezután a négyzet becslési hibák összege a következőképpen fejezhető ki

az OLS becslő az egyszerű regressziós modellben az elfogás és a meredekség becslőpárja, amely minimalizálja a fenti kifejezést. Az OLS-becslések levezetését mindkét paraméterre a könyv 4.1. függeléke tartalmazza. Az eredményeket a Key Concept 4.2 foglalja össze.

az OLS becslő, előre jelzett értékek és maradványok

az OLS becslő a meredekség $\beta_1$ és a lehallgató $\beta_0$ az egyszerű lineáris regressziós modell\az OLS előrejelzett értékek $\widehat{Y}_i$ és maradványok $\hat{u}_i$ a\

a becsült lehallgató $\hat{\beta}_0$, a $\hat{\Beta}_1$ meredekségi paraméter és a $\left(\hat{U}_i\right)$ maradványok $N$ $x_i$ és $y_i$, $I$, $…\ ), \(n$. Ezek a becslések az ismeretlen populáció intercept $\left(\beta_0 \right)$, meredekség $\left(\beta_1\right)$ és hiba kifejezés $(u_i)$.

a fent bemutatott képletek első pillantásra nem feltétlenül intuitívak. A következő interaktív alkalmazás célja, hogy segítsen megérteni az OLS mechanikáját. A megfigyeléseket a koordinátarendszerbe kattintva adhatja meg, ahol az adatokat pontok képviselik. Ha két vagy több megfigyelés áll rendelkezésre, az alkalmazás kiszámítja a regressziós vonalat az OLS és néhány statisztika segítségével, amelyek a jobb oldali panelen jelennek meg. Az eredmények frissülnek, amikor további megfigyeléseket ad hozzá a bal oldali panelhez. A dupla kattintás visszaállítja az alkalmazást, azaz az összes adat eltávolításra kerül.

számos lehetséges módja van a $\hat{\beta}_0$ és $\hat{\beta}_1$ kiszámításának R-ben.például megvalósíthatjuk a 4.2 Kulcsfogalomban bemutatott képleteket R két legalapvetőbb funkciójával: mean() és sum (). Mielőtt ezt megtenné, csatoljuk a CASchools adatkészletet.

attach(CASchools) # allows to use the variables contained in CASchools directly# compute beta_1_hatbeta_1 <- sum((STR - mean(STR)) * (score - mean(score))) / sum((STR - mean(STR))^2)# compute beta_0_hatbeta_0 <- mean(score) - beta_1 * mean(STR)# print the results to the consolebeta_1#> -2.279808beta_0#> 698.9329

Calling attach (CASchools) lehetővé teszi számunkra, hogy címezze a változó szereplő CASchools a nevét: már nem szükséges a $ operátort az adatkészlettel együtt használni: R közvetlenül értékelheti a változó nevét.

R használja az objektumot a felhasználói környezetben, ha ez az objektum megosztja a csatolt adatbázisban található változó nevét. Jobb azonban, ha mindig megkülönböztető neveket használunk az ilyen (látszólag) ambivalenciák elkerülése érdekében!

vegye figyelembe, hogy a mellékelt caschools adatkészletben található változókat közvetlenül a fejezet többi részéhez címezzük!

természetesen még több kézi módszer létezik ezeknek a feladatoknak a végrehajtására. Mivel az OLS az egyik legszélesebb körben alkalmazott becslési technika, az R természetesen már tartalmaz egy lm() (lineáris modell) nevű beépített függvényt, amely felhasználható regresszióanalízis elvégzésére.

a megadandó függvény első argumentuma a plot () – hoz hasonlóan az Y ~ x alapszintaxisú regressziós képlet, ahol y a függő változó, x pedig a magyarázó változó. Az argumentumadatok meghatározzák a regresszióban használandó adatkészletet. Most visszatérünk a könyv példájához, ahol elemezzük a teszteredmények és az osztályméretek közötti kapcsolatot. A következő kód az lm() függvényt használja a könyv 4.3.

# estimate the model and assign the result to linear_modellinear_model <- lm(score ~ STR, data = CASchools)# print the standard output of the estimated lm object to the console linear_model#> #> Call:#> lm(formula = score ~ STR, data = CASchools)#> #> Coefficients:#> (Intercept) STR #> 698.93 -2.28

adjuk hozzá a becsült regressziós vonalat a cselekményhez. Ezúttal mindkét tengely tartományát kibővítjük az xlim és ylim argumentumok beállításával.

# plot the dataplot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)", xlim = c(10, 30), ylim = c(600, 720))# add the regression lineabline(linear_model)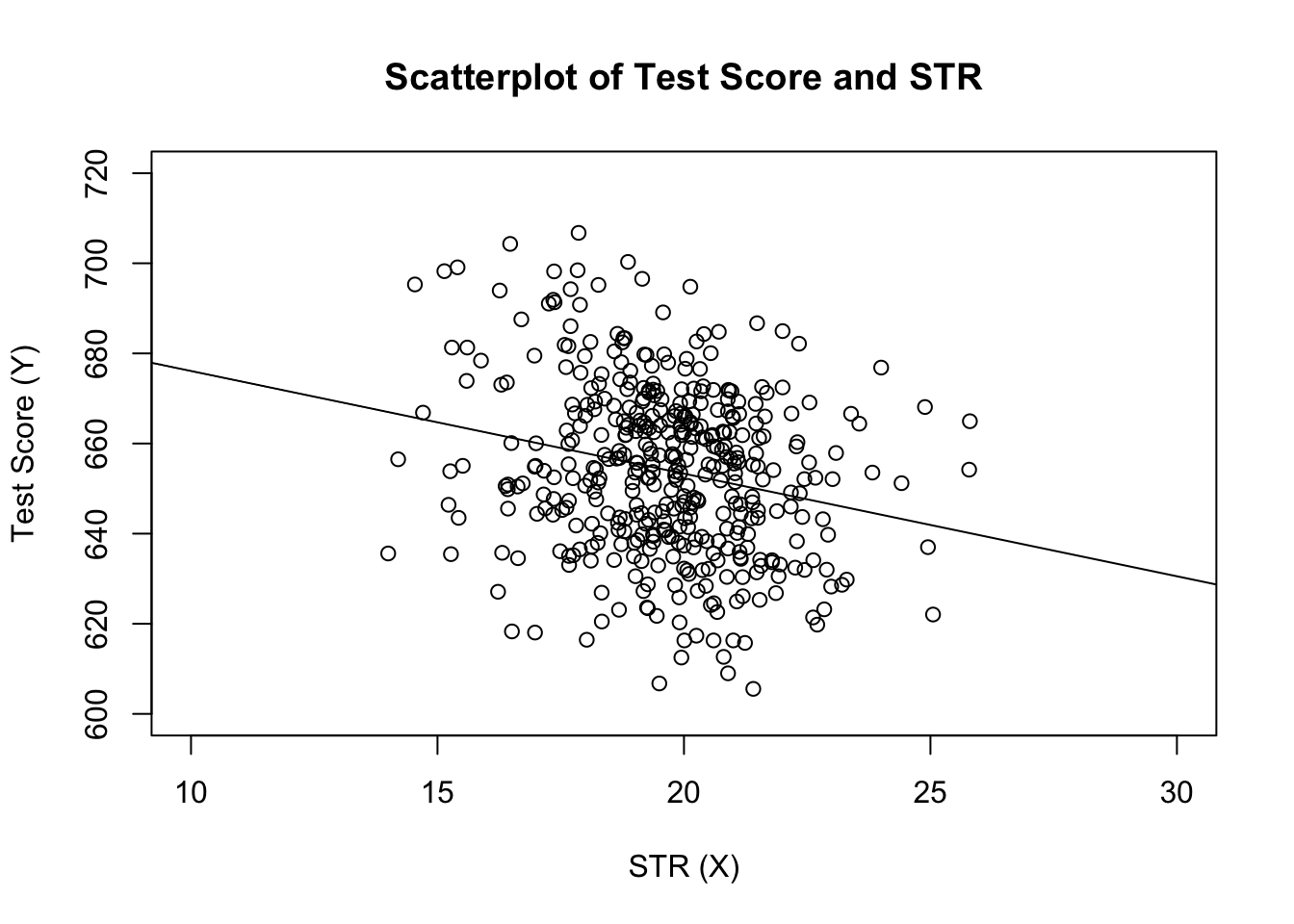

észrevetted, hogy ezúttal nem adtuk át a lehallgatási és lejtési paramétereket abline-nak? Ha az abline () – t egy lm osztályú objektumra hívja, amely csak egyetlen regresszort tartalmaz, R automatikusan meghúzza a regressziós vonalat!