ma lesz egy rövid bevezetés a körkörös statisztika (néha nevezik irányított statisztika). A körkörös statisztika a statisztikák érdekes felosztása, amely magában foglalja az egységkör körüli vektorként vett megfigyeléseket. Például képzelje el a kórházban a születési idő mérését egy 24 órás ciklus alatt, vagy a vándorló állatok csoportjának irányított szétszóródását. Az ilyen típusú adatok különböző területeken vesznek részt, mint például az ökológia, a klimatológia és a biokémia. Az egységkör körüli megfigyelések mérésének jellege a hipotézis tesztelésének más megközelítését teszi szükségessé. Az eloszlásokat a kör köré kell “becsomagolni”, hogy hasznosak legyenek, és a hagyományos becslők, mint például a minta átlaga vagy a minta varianciája, nem tartanak vizet.
ebben a bejegyzésben elvégezzük a Rao Távolságtesztjét a kör alakú adatkészlet egységességének értékelésére. Ez egy alapvető eljárás, amelyet a körkörös adatok kezelésének bevezetéseként kell elképzelni.
első lépések
hipotézis tesztet fogunk végezni teknősökön, egy kis adatkészletet, amely 10 zöld tengeri teknős érkezési szögéből áll fészkelő szigetükre. Célunk annak meghatározása, hogy az érkezési szögek hol mutatják az irányultság jeleit, vagy inkább véletlenszerű szórásra utalnak.
először telepítse a circular csomagot, és csatolja a turtles adatkészletet.
install.packages("circular")require(circular)attach(turtles)
adatok ábrázolása
a circularcsomag saját rajzolási funkciót tartalmaz, plot.circular. Figyeljük meg a teknősök érkezési szögeit.
plot.circular(arrival)
itt van a telek: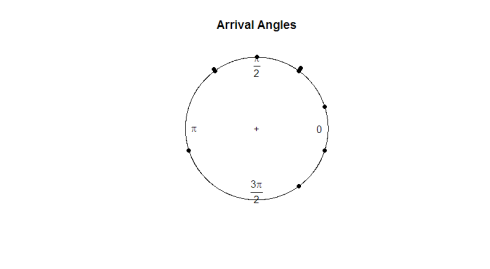
a szemvizsgálat alapján a megfigyelések egységesnek tűnnek a kör körül. Ha hipotézis tesztet akarunk futtatni annak megállapítására, hogy az adatok valóban egységesek-e, akkor ki kell dolgoznunk egy tesztstatisztikát, amely szögadatokkal működik.
mi a jó paraméter számunkra, hogy kihasználja? A mintavételi átlag nem sokat mond nekünk az adatok irányáról (180 fok nem hasznos átlag 2 fok és 358 fok). A következő ábrán, figyelje meg, hogy a minta átlaga hogyan nem használható adataink alakjának vagy terjedésének ábrázolásában.
mean(arrival)plot.circular(mean(arrival)) 0.9120794
itt van a telek: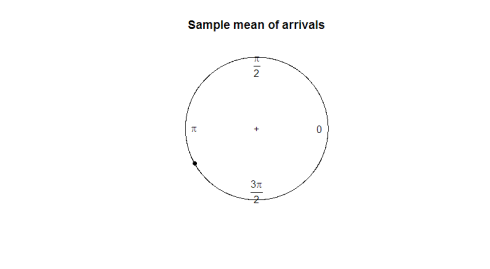
ehelyett olyan módszert fogunk használni, amely meghatározza az irányosságot a megfigyelések közötti átlagos tér mérésével. Ezt a tesztet Rao térköz-tesztnek hívják.
Rao Térköztesztje
A Rao Térköztesztjét a kör alakú adatok egységességének értékelésére fejlesztették ki. A megfigyelések közötti teret használja annak meghatározására, hogy az adatok jelentős irányt mutatnak-e. Ha az adatok egységesek, a megfigyeléseknek általában egyenletesen kell elhelyezkedniük egymástól.
itt van a teszt statisztika \(U\) A Rao térköz tesztjéhez: $$U = 1/2 \ sum \ limits_{i = 1}^n / t_{i} – 6-360, T_{i} = f_{i+1}-F_{i}\) és\ (T_{n} = (360-F_{n})+f_{1}\)
alapvetően a tesztstatisztika összesíti az egymást követő pontok közötti eltéréseket, mindegyiket súlyozva az adatkészletben szereplő megfigyelések teljes számával.
a rao.spacing.test() függvényt fogjuk használni ennek a hipotézis tesztnek a futtatásához. Nullhipotézisünk szerint az adatok egyenletes eloszlásúak, míg az alternatív állapotok az adatok irányultság jeleit mutatják. Futtassuk le a tesztet.
rao.spacing.test(arrival,alpha=.10) Rao's Spacing Test of Uniformity Test Statistic = 127.2689 Level 0.1 critical value = 161.23 Do not reject null hypothesis of uniformity
ha a 127-es tesztstatisztika a 161-es kritikus érték alá esik, az adatok semmilyen irányba nem tudnak jelentősen támaszkodni. Nem utasíthatjuk el azt a hipotézist, hogy a teknősök érkezése egyenletes eloszlású.
következtetés
A Rao térköz-tesztje megállapította, hogy az adatok nem mutatnak irányirányú tendenciákat. Nem utasíthatjuk el az egységesség nullhipotézisét, és az érkezés irányát tekintve egységességet fogunk feltételezni. Bár ez a bejegyzés viszonylag alapvető oktatóanyag volt, az adattudományi közösségben sokan még nem dolgoztak körkörös adatokkal. Érdekes altéma a merülés, valamint egy fiatal statisztikai terület, amely még mindig fejlődik.
Záró megjegyzések
szeretném kiterjeszteni hitelt S. Rao Jammalamadaka PhD, a University of California, Santa Barbara, és a tankönyv “témák körkörös statisztika” szikrázó érdeklődésemet a körkörös statisztika területén.