bármelyik katamorfizmusa a hajtásának általánosítása. A katamorfizmus lehetővé teszi a hajtáson keresztül nem elérhető műveleteket.
ez a cikk a katamorfizmusokról szóló cikksorozat része. A katamorfizmus egy univerzális absztrakció, amely leírja, hogyan lehet egy adatstruktúrát potenciálisan kompaktabb értékké megemészteni.
ez a cikk bemutatja mindkét (más néven eredmény) katamorfizmusát, valamint annak azonosítását. A cikk eleje a katamorfizmust mutatja be C#, példákkal. A cikk többi része leírja, hogyan lehet levezetni a katamorfizmust. A cikknek ez a része a Haskellben végzett munkámat mutatja be. Azok az olvasók, akik nem elégedettek Haskell – lel, csak elolvashatják az első részt, a cikk többi részét pedig opcionális mellékletként tekinthetik meg.
vagy egy adattároló, amely két egymást kizáró eredményt modellez. Gyakran használják olyan értékek visszaadására, amelyek lehetnek helyesek (jobbra) vagy helytelenek (balra). A statikusan gépelt funkcionális programozásban, előnyben részesítve a teljes függvényeket, vagy józanabb, ésszerűbb módszert kínál a siker és a hiba eredményeinek modellezésére, mint a kivételek dobása.
C# catamorphism #
ez a cikk bármelyik egyházi kódolását használja. Az egyik katamorfizmusa a Match módszer:
T Match<T>(Func<L, T> onLeft, Func<R, T> onRight);
e cikkig az összes korábbi katamorfizmus egy kezdeti értékből és egy függvényből álló pár volt. Az egyik katamorfizmus a általánosítás, mivel ez egy pár Funkció. Az egyik függvény a bal oldali értéket, a másik pedig a jobb oldali értéket kezeli. Mindkét függvénynek ugyanazt az egyesítő típust kell visszaadnia, amely gyakran egy karakterlánc vagy valami hasonló, amely a felhasználói felületen megjeleníthető:
> IEither<TimeSpan, int> e = new Left<TimeSpan, int>(TimeSpan.FromMinutes(3));> e.Match(ts => ts.ToString(), i => i.ToString())"00:03:00"> IEither<TimeSpan, int> e = new Right<TimeSpan, int>(42);> e.Match(ts => ts.ToString(), i => i.ToString())"42"
gyakran látni fogja a fentiekhez hasonló példákat, amelyek mind a bal, mind a jobb esetet karakterláncokká változtatják, vagy olyasmit, amely egyesítő választípusként ábrázolható, de ez semmiképpen sem szükséges. Ha előállhat egy egyesítő típussal, mindkét esetet átalakíthatja erre a típusra:
> IEither<Guid, string> e = new Left<Guid, string>(Guid.NewGuid());> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)12> IEither<Guid, string> e = new Right<Guid, string>("foo");> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)3
a fenti két példában két különböző függvényt használ, amelyek mind a Guid, mind a string értékeket számra csökkentik. A Guid értékeket számmá alakító függvény Megszámolja, hogy hány hexadecimális számjegy nagyobb vagy egyenlő a (10) értékkel. A másik függvény egyszerűen visszaadja a string hosszát, ha ott van. Ennek a példának nincs sok értelme, de a Match módszer nem törődik ezzel.
gyakorlati használatban vagy gyakran használják hibakezelésre. Az egyházi kódolásról szóló cikk példát tartalmaz.
vagy F-Algebra #
mint az előző cikkben, fogom használni Fix és cata amint azt Bartosz Milewski kiváló cikket F-algebrák.
míg az F-Algebrákat és a fixpontokat többnyire rekurzív adatstruktúrákhoz használják, definiálhatunk F-algebrát egy nem rekurzív adatstruktúrához is. Erre már láttak példát a logikai katamorfizmusról és talán a katamorfizmusról szóló cikkekben. A különbség például a talán értékek és az egyik között az, hogy mindkét eset értéket hordoz. Ezt Functor – ként modellezheti mind a hordozótípus, mind a két típusú argumentummal az adatokhoz, amelyek bármelyike tartalmazhat:
data EitherF l r c = LeftF l | RightF r deriving (Show, Eq, Read) instance Functor (EitherF l r) where fmap _ (LeftF l) = LeftF l fmap _ (RightF r) = RightF r
az ‘adattípusokat’ l (balra) és r (jobbra), a vivőtípusokat pedig c (hordozóra) hívtam. Mint a BoolF és a MaybeF esetében is, a Functor példány figyelmen kívül hagyja a map függvényt, mert a hordozó típusa hiányzik mind a LeftF, mind a RightF esetből. Mint a Functor példányok BoolF és MaybeF, úgy tűnik, hogy semmi sem történik, de a típus szintjén ez még mindig egy fordítás EitherF l r chogy EitherF l r c1. Nem sok funkció, talán, de határozottan endofunctor.
mint ahogy az a Katamorfizmusok levezetésekor is történt, Haskell nem túl boldog az olyan típusok definiálásában, mint az Fix (EitherF l r). A probléma megoldásához bevezethet egy newtype csomagolót:
newtype EitherFix l r = EitherFix { unEitherFix :: Fix (EitherF l r) } deriving (Show, Eq, Read)
meg lehet határozni Functor, Applicative, Monad, stb. az ilyen típusú példányok anélkül, hogy bármilyen funky GHC kiterjesztést igénybe vennének. Ne feledje, hogy végső soron ennek a kódnak az a célja, hogy kitalálja, hogyan néz ki a katamorfizmus. Ez a kód nem tényleges használatra készült.
egy pár segítő funkció megkönnyíti a EitherFix értékek meghatározását:
leftF :: l -> EitherFix l rleftF = EitherFix . Fix . LeftF rightF :: r -> EitherFix l rrightF = EitherFix . Fix . RightF
ezekkel a függvényekkel EitherFix értékeket hozhat létre:
Prelude Data.UUID Data.UUID.V4 Fix Either> leftF <$> nextRandomEitherFix {unEitherFix = Fix (LeftF e65378c2-0d6e-47e0-8bcb-7cc29d185fad)}Prelude Data.UUID Data.UUID.V4 Fix Either> rightF "foo"EitherFix {unEitherFix = Fix (RightF "foo")}
ez minden, amire szüksége van a katamorfizmus azonosításához.
Haskell katamorfizmus #
ezen a ponton az F-Algebra három eleméből kettő van. Van egy endofunctor (EitherF l r) és egy objektum c, de még mindig meg kell találni a morfizmus EitherF l r c -> c. Figyeljük meg, hogy az algebra meg kell találni a függvény, amely csökkenti a functor annak hordozó típus c, nem az ‘adattípusok’ l és r. Ez eltart egy ideig, hogy megszokja, de így működnek a katamorfizmusok. Ez azonban nem jelenti azt, hogy figyelmen kívül kell hagynod a l és r értéket, ahogy látni fogod.
az előző cikkekhez hasonlóan kezdje el egy olyan funkció megírásával, amely a katamorfizmus, amely alapján cata:
eitherF = cata alg . unEitherFix where alg (LeftF l) = undefined alg (RightF r) = undefined
míg ez lefordítja, a undefined implementációival nyilvánvalóan nem csinál semmi hasznosat. Úgy gondolom azonban, hogy ez segít gondolkodni. Hogyan adhatunk vissza egy c típusú értéket a LeftF esetből? Átadhat egy argumentumot a eitherF függvénynek:
eitherF fl = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = undefined
bár technikailag átadhat egy c típusú argumentumot eitherF – nek, majd visszaadhatja ezt az értéket a LeftF esetből, ez azt jelentené, hogy figyelmen kívül hagyja a l értéket. Ez helytelen lenne, ezért tegyük az argumentumot függvénynek, és hívjuk meg l – val. Hasonlóképpen ugyanúgy kezelheti a RightF esetet:
eitherF :: (l -> c) -> (r -> c) -> EitherFix l r -> ceitherF fl fr = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = fr r
ez működik. Mivel a cata típusa Functor f => (f a -> a) -> Fix f -> a, ez azt jelenti, hogy a algtípusa f a -> a. EitherF esetén a fordító arra következtet, hogy a alg függvény típusa EitherF l r c -> c, amire éppen szüksége van!
most láthatja, hogy mire szolgál a c hordozó típus. Ez az a típus, amelyet az algebra kivonatol,és így a katamorfizmus visszatér.
ez tehát bármelyik katamorfizmusa. Ahogy eddig következetes volt, ez egy pár, de most két funkcióból készült. Mint már többször látta, ez nem az egyetlen lehetséges katamorfizmus, mivel például triviálisan megfordíthatja az argumentumokat eitherFértékre.
azért választottam az itt bemutatott ábrázolást, mert izomorf a Haskell beépített Data.Either moduljának either függvényével, amely a függvényt “Either Típus Esetelemzésének”nevezi. Mindkét függvény (eitherF és either) egyenértékű a fenti C# Match módszerrel.
Basis #
a legtöbb hasznos funkciót a eitherF segítségével valósíthatja meg. Itt van a Bifunctor példány:
instance Bifunctor EitherFix where bimap f s = eitherF (leftF . f) (rightF . s)
ebből a példányból a Functor példány triviálisan következik:
instance Functor (EitherFix l) where fmap = second
a Functor tetejére Applicative:
instance Applicative (EitherFix l) where pure = rightF f <*> x = eitherF leftF (<$> x) f
vegye figyelembe, hogy a <*> megvalósítás hasonló a <*>megvalósításhoz MaybeFix. Ugyanez vonatkozik a Monad példányra:
instance Monad (EitherFix l) where x >>= f = eitherF leftF f x
nem csak EitherFix Foldable, hanem Bifoldable:
instance Bifoldable EitherFix where bifoldMap = eitherF
érdekes módon vegye figyelembe, hogy a bifoldMap megegyezik a eitherF értékkel.
a Bifoldable példány lehetővé teszi a Foldable példány triviálisan történő megvalósítását:
instance Foldable (EitherFix l) where foldMap = bifoldMap mempty
a mempty jelenléte rejtélyes lehet, mivel bifoldMap(vagy eitherF; azonosak) argumentumként két függvényt vesz fel. mempty egy függvény?
Igen, mempty függvény lehet. Tessék, itt van. Van egy Monoid példány bármely a -> m függvényhez, ahol a m egy Monoid példány, a mempty pedig az adott monoid identitása. Ez az itt használt példány.
ahogy EitherFix is Bifoldable, ez is Bitraversable:
instance Bitraversable EitherFix where bitraverse fl fr = eitherF (fmap leftF . fl) (fmap rightF . fr)
kényelmesen megvalósíthatja a Traversable példányt a Bitraversable példány alapján:
instance Traversable (EitherFix l) where sequenceA = bisequenceA . first pure
végül megvalósíthatja a konverziókat a szabványos Either típusra, a ana használatával cata:
toEither :: EitherFix l r -> Either l rtoEither = eitherF Left Right fromEither :: Either a b -> EitherFix a bfromEither = EitherFix . ana coalg where coalg (Left l) = LeftF l coalg (Right r) = RightF r
ez azt mutatja, hogy EitherFix izomorf a Either – vel, ami ismét megállapítja, hogy eitherF és either ekvivalensek.
Relationships #
ebben a sorozatban számos példát láthattunk a redők nélküli struktúrák katamorfizmusaira, a redőkkel egybeeső katamorfizmusokra, és most egy olyan katamorfizmusra, amely általánosabb, mint a redő. A sorozat bevezetése tartalmazta ezt a diagramot:
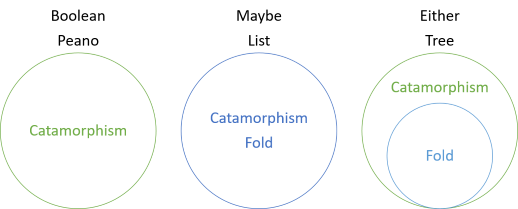
ez azt mutatja, hogy a Boole-értékek és a Peano-számok katamorfizmussal rendelkeznek, de nincsenek redők, míg a Maybe és List esetében a redő és a katamorfizmus ugyanaz. Mindkettő számára azonban a hajtás a katamorfizmus különleges esete. A hajtás mindkét ‘úgy tesz, mintha’, hogy a bal oldalon nem létezik. Ehelyett a bal oldali értéket hiányzó jobb értékként értelmezik. Így, annak érdekében, hogy hajtsa mindkét értéket, meg kell adnia egy ‘tartalék’ értéket, amely akkor használható, ha egy érték nem megfelelő érték:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e""
a fentiekhez hasonló GHCi munkamenetben két azonos típusú értéket hozhat létre. A jobb eset Ordering érték, míg a bal eset Integer érték.
foldr esetén nincs mód a bal oldali tok elérésére. Míg elérheti és átalakíthatja a jobb Ordering értéket, a 42 számot egyszerűen figyelmen kívül hagyja a hajtás során. Ehelyett az alapértelmezett "" értéket adja vissza.
kontraszt ez a katamorfizmus, amely hozzáférhet mindkét esetben:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"42"
egy ilyen munkamenetben ugyanazokat az értékeket hozhatja létre, de a eitherF katamorfizmus használatával elérheti és átalakíthatja mind a bal, mind a jobb esetet. Más szavakkal, a katamorfizmus lehetővé teszi a hajtással nem lehetséges műveletek végrehajtását.
érdekes azonban megjegyezni, hogy míg a hajtás a katamorfizmus specializációja, a bifold megegyezik a katamorfizmussal.
Összegzés #
bármelyik katamorfizmusa függvénypár. Az egyik funkció átalakítja a bal esetet, míg a másik funkció átalakítja a jobb esetet. Bármelyik értéknél csak az egyik függvény kerül felhasználásra.
amikor először találkoztam a katamorfizmus fogalmával, nehezen tudtam különbséget tenni a katamorfizmus és a hajtás között. A problémám az volt, azt hiszem, hogy az oktatóanyagok, amelyekbe belefutottam, többnyire összekapcsolt listákat használtak annak bemutatására, hogy ebben az esetben a hajtás a katamorfizmus. Kiderül, azonban, hogy ez nem mindig így van. A katamorfizmus általános absztrakció. A hajtás viszont úgy tűnik számomra, hogy leginkább a gyűjteményekhez kapcsolódik.
ebben a cikkben látta a katamorfizmus első példáját, amely többet tud tenni, mint a hajtás. Mindkét esetben a hajtás csak a katamorfizmus különleges esete. Azt is látta, hogy a katamorfizmus megegyezik a bifolddal. Így még mindig nem teljesen világos, hogy ezek a fogalmak hogyan kapcsolódnak egymáshoz. Ezért a következő cikkben kapsz egy példát egy konténerre, ahol nincs bifold, és ahol a katamorfizmus valójában a hajtás általánosítása.
következő: fa katamorfizmus.