ez egy lépésről lépésre bemutatja, hogyan kell futtatni a K-means cluster analysis-t egy Excel-táblázatban az elejétől a végéig. Felhívjuk figyelmét, hogy van egy Excel sablon, amely automatikusan futtatja a klaszterelemzést, ingyenesen letölthető ezen a weboldalon. De ha szeretné tudni, hogyan kell futtatni egy k-means fürtözést az Excel-en, akkor ez a cikk az Ön számára.
ezen a cikken kívül van egy videó áttekintésem arról is, hogyan kell futtatni a klaszterelemzést az Excelben.
- első lépés-Kezdje az adatkészlettel
- második lépés-ha csak két változó, használjon scatter gráfot az Excelben
- harmadik lépés-Számítsa ki az egyes adatpontoktól a fürt középpontjáig tartó távolságot
- hogyan működik a számítás?
- negyedik lépés-Számítsa ki az egyes klaszterkészletek átlagát (átlagát)
- ötödik lépés-ismételje meg a 3. lépést-a felülvizsgált átlagtól való távolság
- végső lépés-gráf és a klaszterek összefoglalása
első lépés-Kezdje az adatkészlettel
ábra 1
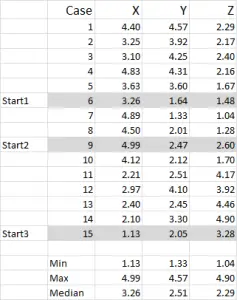
ebben a példában 15 esetet (vagy válaszadókat) használok, ahol három változó adatai vannak – általában X, Y és Z.
észre kell vennie, hogy az adatok ebben a példában 1-5-re vannak méretezve. Adatai bármilyen formában lehetnek, kivéve a névleges adatskálát(lásd a milyen adatokat kell használni).
megjegyzés: inkább skálázott adatokat használok – de ez nem kötelező. Ennek oka az, hogy” tartalmazzon ” minden kiugró értéket. Tegyük fel például, hogy jövedelemadatokat (demográfiai mértéket) használok – az adatok többsége körülbelül 40 000-100 000 dollár lehet, de van egy olyan személyem, akinek jövedelme 5 millió dollár. egyszerűen könnyebb osztályoznom ezt a személyt a “több mint 250 000 dollár” jövedelemcsoportba és az 1-9 – es jövedelem skálájába-de ez rajtad múlik, attól függően, hogy milyen adatokkal dolgozik.
ebből a példakészletből látható, hogy három kezdő pozíció került kiemelésre – ezeket az alábbi harmadik lépésben tárgyaljuk.
második lépés-ha csak két változó, használjon scatter gráfot az Excelben
ábra 2
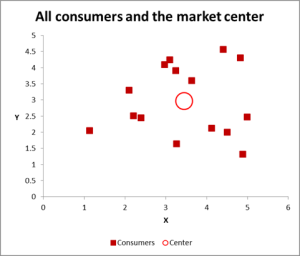
ebben a klaszterelemzési példában három változót használunk – de ha csak két változót kell fürtöznie, akkor a szórási diagram kiváló módja a kezdésnek. Időnként vizuális eszközökkel csoportosíthatja az adatokat.
mint látható ebben a szórási grafikonban, minden egyes esetet (amit ebben a példában fogyasztónak hívok) leképeztünk, az összes eset átlagával (átlagával) együtt (a piros kör).
az adatok/grafikon megtekintésének módjától függően-úgy tűnik, hogy számos klaszter van. Ebben az esetben három vagy négy viszonylag különálló klasztert azonosíthat – amint azt a következő diagram mutatja.
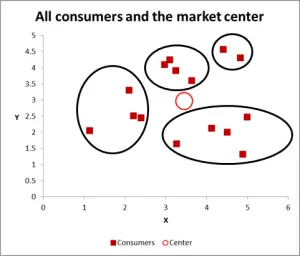
ábra 3
ezzel a következő grafikonnal láthatóan azonosítottam a valószínű klasztert, és köröztem őket. Mint javasoltam, jó megközelítés, ha csak két változót kell figyelembe venni – de ebben az esetben három változónk van (és lehet, hogy több is van), tehát ez a vizuális megközelítés csak az alapadatkészleteknél fog működni-tehát most nézzük meg, hogyan kell elvégezni az Excel számítást k-azt jelenti, hogy a klaszterezés.
harmadik lépés-Számítsa ki az egyes adatpontoktól a fürt középpontjáig tartó távolságot
ehhez az áttekintő példához tegyük fel, hogy csak három szegmenst/klasztert akarunk azonosítani. Igen, a fenti ábrán négy klaszter látható, de ez csak kettőt vizsgál a változók közül. Felhívjuk figyelmét, hogy ezzel az Excel – megközelítéssel annyi klasztert azonosíthat, amennyit csak akar-csak kövesse ugyanazt a koncepciót, mint az alábbiakban.
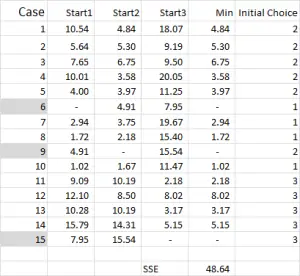
ábra 4
a k-azt jelenti, hogy a klaszterezés általában véletlenszerű eseteket (kiindulási pontokat vagy magokat) választ ki az elemzés megkezdéséhez.
ebben a példában-mivel három klasztert akarok létrehozni, akkor három kiindulási pontra lesz szükségem. Ezekre a kiindulási pontokra a 6., a 9. és a 15. esetet választottam – de bármilyen véletlenszerű pont is megfelelő lehet.
azért választottam ezeket az eseteket, mert – ha csak az X változót nézzük – a 6.eset volt a medián, a 9. eset volt a maximális, a 15. eset pedig a minimális. Ez arra utal, hogy ez a három eset némileg különbözik egymástól, olyan jó kiindulópontok, mivel szét vannak osztva.
kérjük, olvassa el a cikket arról, hogy a klaszterelemzés miért generál néha különböző eredményeket.
a táblázat kimenetére utalva – ez az első számításunk az Excelben, és létrehozza a klaszterek “kezdeti választását”. Az 1. indítás a 6.eset adatai, a 2. indítás a 9. eset, a 3. indítás pedig a 15. eset. Meg kell jegyezni, hogy ezek metszéspontja 0 (-) értéket ad a táblázatban.
hogyan működik a számítás?
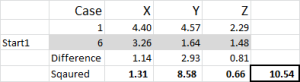
ábra 5
nézzük meg a táblázat első számát-1. eset, 1 = 10,54.
ne feledje, hogy önkényesen kijelöltük a 6. esetet az 1. klaszter véletlenszerű kiindulópontjának. Ki akarjuk számítani a távolságot, és a négyzetek összege módszert használjuk – amint az itt látható. Kiszámítjuk a halmaz mindhárom adatpontja közötti különbséget, majd négyzetezzük a különbségeket, majd összegezzük őket.
meg tudjuk csinálni “mechanikusan”, amint az itt látható – de az Excel beépített képlettel rendelkezik: SUMXMY2-ez sokkal hatékonyabb a használata.
visszatérve a 4. ábrára, ezután megtaláljuk az egyes esetek minimális távolságát a három kiindulási ponttól – ez megmondja, hogy melyik klaszterhez (1, 2 vagy 3) van a legközelebb az eset–, amely a ‘kezdeti választási oszlopban’látható.
negyedik lépés-Számítsa ki az egyes klaszterkészletek átlagát (átlagát)
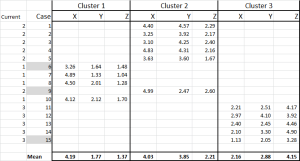
ábra 6
most minden esetet hozzárendeltünk a kezdeti klaszteréhez – és ezt egy IF utasítás segítségével egy táblázatban (amint azt a 6.ábra mutatja).
a táblázat alján ezen esetek átlaga (átlaga) található. N0w – ahelyett, hogy csak egy “reprezentatív” adatpontra támaszkodnánk-van egy sor esetünk, amelyek mindegyiket képviselik.
ötödik lépés-ismételje meg a 3. lépést-a felülvizsgált átlagtól való távolság
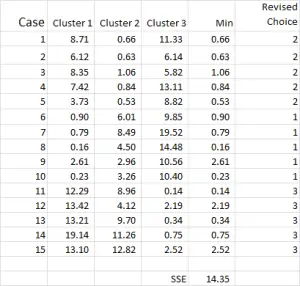
ábra 7
a klaszterelemzési folyamat most a 4.és 5. lépés (iterációk) megismétlésének kérdésévé válik, amíg a klaszterek stabilizálódnak.
minden alkalommal, amikor az egyes klaszterek felülvizsgált átlagát használjuk. Ezért a 7. ábra a második iterációnkat mutatja-de ezúttal a 6. ábra alján generált eszközöket használjuk (az 1.ábra kezdőpontjai helyett).
most már láthatja, hogy a klaszteralkalmazásban enyhe változás történt, a 9.eset – az egyik kiindulási pontunk – átcsoportosításra került.
a négyzethiba összege (SSE) is látható az alján – ami az egyes minimális távolságok összege. Célunk, hogy most megismételjük a 4.és 5. lépést, amíg az SSE csak minimális javulást nem mutat, és/vagy a klaszter allokációs változások minden iterációnál kisebbek lesznek.
végső lépés-gráf és a klaszterek összefoglalása
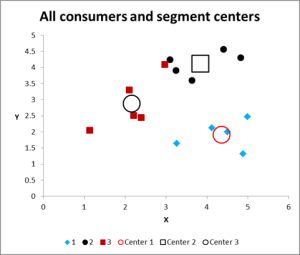
ábra 8
több iteráció futtatása után most már megvan a kimenet az adatok grafikonjára és összefoglalására.
itt található a klaszteranalízis Excel példájának kimeneti grafikonja.
mint látható, három különálló klaszter látható, az egyes klaszterek centroidjaival (átlagával) együtt – a nagyobb szimbólumokkal.
ezeket az adatokat táblázatos formában is bemutathatjuk, ha szükséges, mivel az Excelben dolgoztuk ki.
kérjük, vessen egy pillantást a 3.klaszter esetére – a kis piros négyzet közvetlenül a fekete pont mellett a grafikon felső közepén. Ez az eset a harmadik változó hatása miatt áll, amely nem jelenik meg ezen a két változó diagramon.