dit is een stapsgewijze handleiding voor het uitvoeren van K-means clusteranalyse op een Excel-spreadsheet van begin tot eind. Houd er rekening mee dat er een Excel-sjabloon is dat automatisch clusteranalyse uitvoert en gratis te downloaden is op deze website. Maar als je wilt weten hoe je zelf een k-means clustering op Excel uitvoert, dan is dit artikel iets voor jou.
naast dit artikel heb ik ook een video walk-through van het uitvoeren van clusteranalyse in Excel.
- Stap 1-Begin met uw gegevensverzameling
- stap twee – indien slechts twee variabelen, gebruik een spreidingsgrafiek op Excel
- Stap drie-Bereken de afstand van elk gegevenspunt tot het centrum van een cluster
- Hoe werkt de berekening?
- Stap vier-Bereken het gemiddelde (gemiddelde) van elke clusterset
- Stap vijf-Herhaal stap 3 – de afstand tot het herziene gemiddelde
- Laatste Stapgrafiek en samenvatting van de Clusters
Stap 1-Begin met uw gegevensverzameling
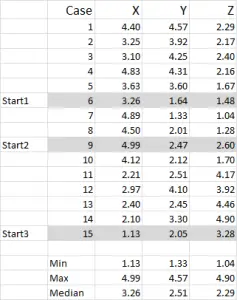
figuur 1
voor dit voorbeeld gebruik ik 15 gevallen (of respondenten), waar we de gegevens voor drie variabelen hebben – in het algemeen aangeduid met X, Y en Z.
u moet merken dat de gegevens in dit voorbeeld 1-5 worden geschaald. Uw gegevens kunnen in om het even welke vorm zijn behalve voor een nominale gegevensschaal (zie artikel van welke gegevens te gebruiken).
opmerking: Ik gebruik liever geschaalde gegevens – maar het is niet verplicht. De reden hiervoor is om eventuele uitschieters “in te houden”. Zeg, bijvoorbeeld, Ik ben met behulp van inkomensgegevens – een demografische maatregel) – de meeste van de gegevens zou kunnen worden rond $40.000 tot $100.000, maar ik heb een persoon met een inkomen van $5m. het is gewoon makkelijker voor mij om die persoon te classificeren in de “meer dan $250.000” inkomensschijf en schaal inkomen 1-9-maar dat is aan u, afhankelijk van de gegevens die u werkt met.
u kunt uit deze voorbeeldset zien dat er drie startposities zijn gemarkeerd – we zullen deze in Stap drie hieronder bespreken.
stap twee – indien slechts twee variabelen, gebruik een spreidingsgrafiek op Excel
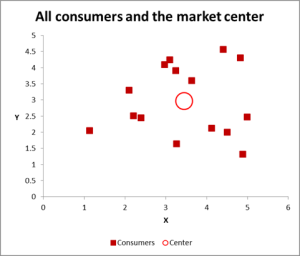
Figuur 2
In dit voorbeeld van clusteranalyse gebruiken we drie variabelen – maar als u slechts twee variabelen hebt om te clusteren, dan is een spreidingsdiagram een uitstekende manier om te beginnen. En soms kunt u de gegevens via visuele middelen clusteren.
zoals u kunt zien in deze spreidingsgrafiek, is elk individueel geval (wat ik een consument noem voor dit voorbeeld) in kaart gebracht, samen met het gemiddelde (gemiddelde) voor alle gevallen (de rode cirkel).
afhankelijk van hoe u de gegevens/grafiek bekijkt-er lijken een aantal clusters te zijn. In dit geval kunt u drie of vier relatief verschillende clusters identificeren – zoals weergegeven in deze volgende grafiek.
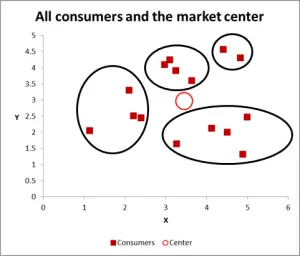
Figuur 3
met deze volgende grafiek heb ik de waarschijnlijke cluster zichtbaar geïdentificeerd en omcirkeld. Zoals Ik heb voorgesteld, een goede aanpak als er slechts twee variabelen zijn om te overwegen – maar is dit het geval hebben we drie variabelen (en je zou meer kunnen hebben), dus deze visuele benadering zal alleen werken voor basisgegevensverzamelingen – dus laten we nu kijken naar hoe je de Excel berekening voor k-betekent clustering doen.
Stap drie-Bereken de afstand van elk gegevenspunt tot het centrum van een cluster
voor dit doorloopvoorbeeld, laten we aannemen dat we alleen drie segmenten/clusters willen identificeren. Ja, er zijn vier clusters duidelijk in het diagram hierboven, maar dat kijkt alleen naar twee van de variabelen. Houd er rekening mee dat u deze Excel – benadering kunt gebruiken om zoveel clusters te identificeren als u wilt-volg gewoon hetzelfde concept als hieronder wordt uitgelegd.
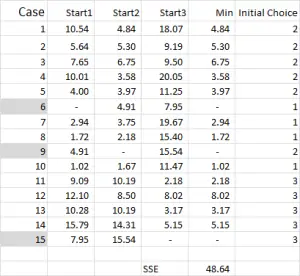
Figuur 4
voor k-means clustering kies je meestal een aantal willekeurige gevallen (startpunten of zaden) om de analyse te starten.
in dit voorbeeld – omdat ik drie clusters wil maken, heb ik drie startpunten nodig. Voor deze startpunten heb ik gevallen 6, 9 en 15 geselecteerd – maar willekeurige punten kunnen ook geschikt zijn.
de reden dat ik deze gevallen heb gekozen is omdat – wanneer alleen naar variabele X wordt gekeken – geval 6 de mediaan was, geval 9 het maximum en geval 15 het minimum. Dit suggereert dat deze drie gevallen enigszins verschillen van elkaar, dus goede uitgangspunten als ze worden verspreid.
zie het artikel Waarom clusteranalyse soms verschillende resultaten oplevert.
verwijzend naar de tabeluitvoer – dit is onze eerste berekening in Excel en het genereert onze “initiële keuze” van clusters. Start 1 is de data voor geval 6, start 2 is Geval 9 en start 3 is Geval 15. U moet er rekening mee houden dat het snijpunt van elk van deze geeft een 0 (-) in de tabel.
Hoe werkt de berekening?
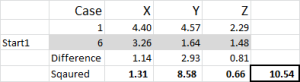
Figuur 5
laten we eens kijken naar het eerste getal in de tabel – geval 1, Begin 1 = 10,54.
onthoud dat we willekeurig geval 6 hebben aangewezen als ons willekeurige startpunt voor Cluster 1. We willen de afstand berekenen en we gebruiken de kwadratensom-methode – zoals hier getoond. We berekenen het verschil tussen elk van de drie gegevenspunten in de verzameling, en dan kwadrateren de verschillen, en dan optellen ze.
we kunnen het “mechanisch” doen zoals hier getoond – maar Excel heeft een ingebouwde formule om te gebruiken: SUMXMY2-dit is veel efficiënter om te gebruiken.
verwijzend naar figuur 4, vinden we dan de minimale afstand voor elk geval van elk van de drie beginpunten – dit vertelt ons welke cluster (1, 2 of 3) dat het geval het dichtst bij – die wordt weergegeven in de “eerste keuze kolom”.
Stap vier-Bereken het gemiddelde (gemiddelde) van elke clusterset
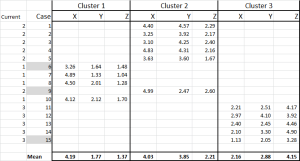
Figuur 6
we hebben nu elk geval toegewezen aan zijn initiële cluster – en we kunnen dat uit te leggen met behulp van een IF-statement in een tabel (zoals weergegeven in Figuur 6).
onderaan de tabel hebben we het gemiddelde (gemiddelde) van elk van deze gevallen. N0w-in plaats van te vertrouwen op slechts één “representatief” gegevenspunt – hebben we een reeks gevallen die elk vertegenwoordigen.
Stap vijf-Herhaal stap 3 – de afstand tot het herziene gemiddelde
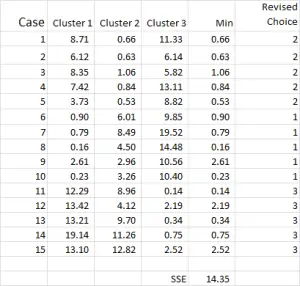
Figuur 7
het proces van de clusteranalyse wordt nu een kwestie van het herhalen van stappen 4 en 5 (iteraties) totdat de clusters stabiliseren.
elke keer dat we het herziene gemiddelde voor elk cluster gebruiken. Daarom toont figuur 7 Onze tweede iteratie – maar deze keer gebruiken we de middelen gegenereerd aan de onderkant van Figuur 6 (in plaats van de startpunten van Figuur 1).
u kunt nu zien dat er een kleine verandering is opgetreden in clustertoepassing, waarbij geval 9 – een van onze uitgangspunten – opnieuw is toegewezen.
u kunt ook de som van de kwadraatfout (SSE) zien die onderaan wordt berekend-wat de som is van elk van de minimumafstanden. Ons doel is om nu te herhalen stappen 4 en 5 totdat de SSE toont slechts minimale verbetering en / of de cluster allocatiewijzigingen zijn klein op elke iteratie.
Laatste Stapgrafiek en samenvatting van de Clusters
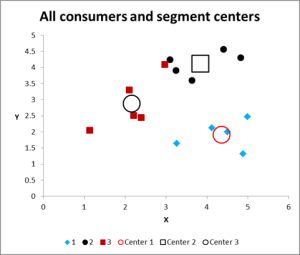
Figuur 8
na het uitvoeren van meerdere iteraties, hebben we nu de output om grafiek en samenvatting van de gegevens.
hier is de uitvoergrafiek voor dit clusteranalyse Excel voorbeeld.
zoals u kunt zien, zijn er drie verschillende clusters weergegeven, samen met de centroids (gemiddelde) van elke cluster – de grotere symbolen.
we kunnen deze gegevens indien nodig ook in een tabelvorm presenteren, zoals we het in Excel hebben uitgewerkt.
kijk eens naar het geval in Cluster 3 – het kleine rode vierkantje naast de zwarte stip in het bovenste midden van de grafiek. Dat geval zit daar vanwege de invloed van de derde variabele, die niet wordt weergegeven op deze twee variabele grafiek.