Conocimiento asumido
Los estudiantes habrán tenido una amplia experiencia informal con la geometría en años anteriores, y esto proporcionará una buena base intuitiva para el enfoque más sistemático de la geometría apropiado en los Años 7-10. Los temas particulares de los años F a 6 relevantes para este módulo son:
- El uso de brújulas y reglas y el cuidadoso dibujo de figuras geométricas.
- Tipos de ángulos, incluidos al menos los ángulos rectos, agudos, obtusos y
ángulos reflejos. - Triángulos, incluyendo una introducción informal a los isósceles y triángulos equiláteros.
- Cuadriláteros, incluyendo una introducción informal a cuadrados, rectángulos, paralelogramos, trapecios y rombos.
- Experiencia informal con traducciones, reflexiones, rotaciones y ampliaciones,
y con simetría en el contexto de actividades como plegar un triángulo isósceles, un rectángulo o un rombo.
Motivación
se utiliza para modelar el mundo que nos rodea. Una vista de los techos de las casas revela triángulos, trapecios y rectángulos, mientras que los patrones de baldosas en pavimentos y baños usan hexágonos, pentágonos, triángulos y cuadrados.
Constructores, azulejos, arquitectos, diseñadores gráficos y diseñadores web utilizan habitualmente ideas geométricas en su trabajo. La clasificación de estos objetos geométricos y el estudio de sus propiedades son muy importantes. La geometría también tiene muchas aplicaciones en el arte.
Así como la aritmética tiene los números como objetos básicos de estudio, los puntos, las líneas y los círculos son los bloques de construcción básicos de la geometría plana.
En la geometría de la escuela secundaria, comenzamos con una serie de ideas intuitivas (puntos, líneas y ángulos) que no son fáciles de definir con precisión, seguidas de algunas definiciones (ángulos opuestos verticalmente, líneas paralelas, etc.) y de éstas deducimos hechos importantes, que a menudo se conocen como teoremas. En la escuela secundaria, el nivel de rigor debe evolucionar lentamente de un año a otro, pero en cada etapa es muy importante establecer un planteamiento claro que debe destacarse.
Por lo tanto, la geometría da una oportunidad para que los estudiantes desarrollen su intuición geométrica, que tiene aplicaciones en muchas áreas de la vida, y también para aprender a construir argumentos lógicos y hacer deducciones en un entorno que es, en su mayor parte, independiente
de número.
Contenido
Puntos y líneas
Los objetos más simples en geometría plana son puntos y líneas. Debido a que son tan simples, es difícil dar definiciones precisas de ellos, por lo que en su lugar, nuestro objetivo es dar a los estudiantes una descripción aproximada de sus propiedades que estén en línea con nuestra intuición. Un punto marca una posición pero no tiene tamaño. En la práctica, cuando dibujamos un punto, claramente tiene un ancho definido, pero representa un punto en nuestra imaginación. Una línea no tiene ancho y se extiende infinitamente en ambas direcciones. Cuando dibujamos una línea, tiene ancho y extremos, por lo que no es realmente una línea, sino que representa una línea en nuestra imaginación. Dados dos puntos distintos A y B, entonces hay una (y solo una) línea que pasa a través de ambos puntos. Usamos letras mayúsculas para referirnos a puntos y líneas de nombre, ya sea indicando dos puntos en la línea, o usando letras pequeñas como 
y m. Por lo tanto, la línea dada a continuación se conoce como la línea AB o como la línea .
Dadas dos líneas distintas, hay dos posibilidades: pueden encontrarse en un solo punto o nunca, sin importar cuánto se extiendan (o se produzcan). Las líneas que nunca se encuentran se llaman paralelas. En el segundo diagrama, escribimos AB / / CD.
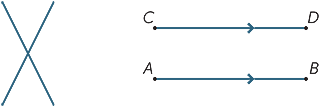
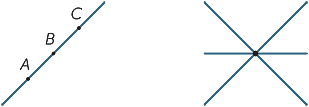
Tres (o más) puntos que se encuentran en una línea recta se denominan colineales.
Tres (o más) líneas que se encuentran en un solo punto se denominan concurrentes.
|
|
|
| Colineal |
Concurrente |
Ejercicio 1
Dibuja tres líneas que no sean simultáneas, de modo que no haya dos paralelas.
Ejercicio 2
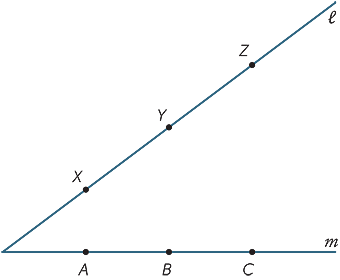
Haga una copia grande del diagrama a continuación. Los puntos X, Y, Z son cualquier punto de la línea y A, B, C son cualquier punto de la línea m. Join AY y XB llaman a su intersección R. Join BZ e YC y llaman a su intersección P. Join CX y Z y llaman a su intersección Q. ¿Qué nota de los puntos P, Q, R? (Este resultado se llama teorema de Pappus, c. 340 DC.)
Intervalos, Rayos y ángulos
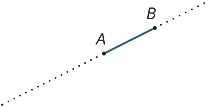Supongamos que A y B son dos puntos en una línea. El intervalo
AB es la parte de la línea entre A y B, incluidos los dos extremos.
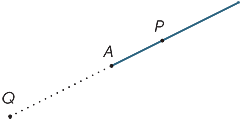El punto A en el diagrama divide la línea en dos piezas llamadas rayos. El rayo AP es el rayo que contiene el punto P (y el punto A).
Ángulos
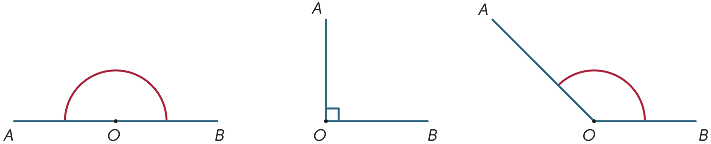
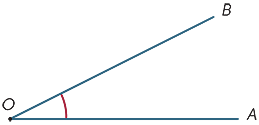
En el diagrama, la región sombreada entre los rayos OA y OB se denomina ángulo AOB o ángulo BOA. El signo de ángulo 
se escribe así que escribimos AOB.
La región sombreada exterior se denomina ángulo reflejo formado por OA y OB. La mayoría de las veces, a menos que especifiquemos la palabra reflejo, todos nuestros ángulos se refieren al área entre los rayos y no fuera de ellos.
El tamaño de un ángulo
Imagine que el rayo OB gira alrededor del punto O hasta que se encuentra a lo largo de OA. La cantidad de giro se llama el tamaño del ángulo AOB. Podemos definir de manera similar el tamaño del ángulo reflejo.
A menudo usaremos letras griegas pequeñas, α, β, γ,… para representar el tamaño de un ángulo.
El tamaño del ángulo correspondiente a una revolución completa fue dividido (por los babilonios) en 360 partes iguales, que llamamos grados. (Probablemente eligieron 360, ya que estaba cerca del número de días en un año. Por lo tanto, el tamaño de un ángulo recto es de 180° y el tamaño de un ángulo recto es de 90°. Otros ángulos se pueden medir (aproximadamente) usando un transportador.
|
|
||
| ángulo Recto | ángulo recto |
ángulo Obtuso |
los Ángulos se clasifican de acuerdo a su tamaño. Decimos que un ángulo con tamaño α es agudo
(una palabra que significa «agudo») si 0° < α < 90°, α es obtuso (una palabra que significa «romo») si
90° < α < 180° y α es reflejo si 180° < α < 360°.
Dado que el transportador tiene dos escalas, los estudiantes deben tener cuidado al dibujar y medir ángulos
. Es un ejercicio que vale la pena usar un transportador para dibujar algunos ángulos, como 30°, 78°, 130°, 163°.
Ejercicio 3
Doble una hoja de papel A4 que coincida con las esquinas opuestas (en diagonal). Dibuja una línea a lo largo del pliegue que se forma y mide los ángulos entre el pliegue y el lado.
En el ejercicio anterior, los dos ángulos juntos forman una línea recta y, por lo tanto, se suman a 180°. Dos ángulos que suman 180° se denominan ángulos suplementarios; por lo tanto, 45° y 135° son ángulos suplementarios.
Dos ángulos que suman 90° se llaman complementarios; por lo tanto, 23° y 67° son
ángulos complementarios.
Ángulos en un punto
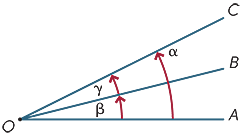Se dice que dos ángulos en un punto son adyacentes si comparten un rayo común. Por lo tanto, en el diagrama, AOB y BOC son adyacentes.
Se pueden agregar ángulos adyacentes, por lo que en el diagrama
α = β + γ.
Cuando dos rectas se cruzan, se forman cuatro ángulos en el punto de intersección.
En el diagrama, los ángulos marcados AOX y BOY se llaman verticalmente opuestos.
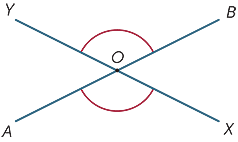Desde
- AOX es el suplemento de BOX (ángulo recto).
-
BOY es también el suplemento de BOX (ángulo recto),
podemos concluir que estos ángulos verticalmente opuestos,
AOX y BOY son iguales. Por lo tanto, tenemos nuestra primera declaración geométrica importante
:
Los ángulos verticalmente opuestos son iguales.
Un resultado en geometría (y en matemáticas en general) a menudo se llama teorema. Un teorema es una declaración importante que puede ser probada por deducción lógica. El argumento anterior es una prueba del teorema; a veces las pruebas se presentan formalmente después de la declaración del teorema.
Si dos rectas se cruzan para que los cuatro ángulos sean rectos, entonces se dice que las rectas son perpendiculares.
Ángulos en un punto-Argumentos geométricos
Las siguientes razones se pueden usar en argumentos geométricos:
- Los ángulos adyacentes se pueden sumar o restar.
- Los ángulos en una revolución se suman a 360°.
- Los ángulos en línea recta suman 180°.
- Los ángulos verticalmente opuestos son iguales.
Transversales y Líneas paralelas
Una línea transversal es una línea que se encuentra con otras dos líneas.
Ángulos correspondientes
Varios ángulos están formados por la transversal. En los diagramas de abajo, los dos ángulos marcados se llaman ángulos correspondientes.
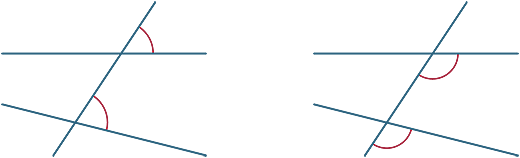
Ahora vemos lo que sucede cuando las dos líneas cortadas por la transversal son paralelas.
Inituitivamente, si el ángulo α fuera mayor que β, entonces CD cruzaría AB a la izquierda de F y si fuera menor que β, cruzaría a la derecha de F. Por lo tanto, dado que las líneas no se cruzan en absoluto, α no puede ser ni menor ni mayor que β y, por lo tanto, es igual a β.
Alternativamente, imagine traducir el ángulo QGD a lo largo de GF hasta que G coincida con F. Dado que las líneas son paralelas, esperaríamos que el ángulo α coincidiera con el ángulo β. Esta observación nos lleva a conjeturar que:
Los ángulos correspondientes formados por líneas paralelas son iguales.
No podemos probar este resultado, aunque hemos demostrado que es geométricamente plausible. Lo aceptaremos como un axioma de la geometría. Un axioma es una afirmación que no podemos probar, pero que es intuitivamente razonable. Tenga en cuenta que muchos de los hechos que ya hemos indicado, como: se pueden agregar ángulos adyacentes, y dos puntos determinan una línea, etc., también son axiomas, aunque no los hemos declarado explícitamente de esta manera.
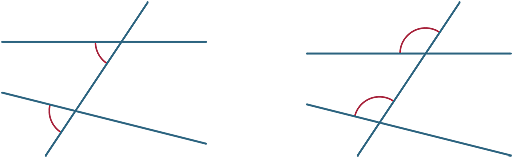
Ángulos alternos
En cada diagrama, los dos ángulos marcados se denominan ángulos alternos (ya que están en lados alternos de la transversal).
Si las líneas AB y CD son paralelas, los ángulos alternativos son iguales. Este resultado ahora se puede probar.
DGQ = α (ángulos correspondientes, AB / / CD)
DGQ = β (ángulos verticalmente opuestos en G)
So α = β.
Para resumir:
Los ángulos alternos formados por líneas paralelas son iguales.
Ángulos co-interiores
Finalmente, en cada diagrama a continuación, los dos ángulos marcados se denominan ángulos co-interiores y se encuentran en el mismo lado de la transversal.
Si las líneas AB y CD son paralelas, entonces es obvio que los ángulos co-interiores no son iguales, pero resulta que son suplementarios, es decir, su suma es de 180° .
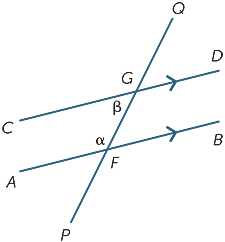Este es un resultado que también es fácil de probar:
BFG = β (ángulos alternos, AB ||CD)
α + β = 180° (ángulo recto a F)
En resumen:
Los ángulos Co-interiores formados a partir de líneas paralelas son suplementarios.
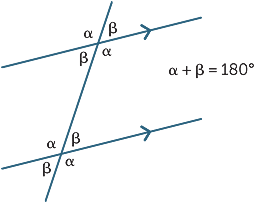Los tres resultados se pueden resumir
mediante el siguiente diagrama:
Ejemplos numéricos
Dada la información sobre los ángulos en un diagrama, podemos usar los resultados anteriores para encontrar el tamaño de otros ángulos en el diagrama. Esta es una habilidad simple pero muy importante, a menudo conocida informalmente como persecución en ángulo. Al resolver problemas, la secuencia de pasos no siempre es única. Puede haber varios enfoques diferentes, pero igualmente válidos.
Por ejemplo, en el siguiente diagrama, buscamos el tamaño del ángulo BAC.
DCA = 102° (ángulos alternos, AC / BD)
BAC = 78° (ángulos co-interiores, AB / / CD)
Ejercicio 4
Use una secuencia de pasos alternos para encontrar BAC.
Ejercicio 5
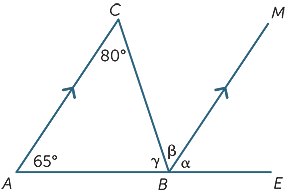Usando solo las propiedades de las líneas paralelas, encuentre (con las razones) los ángulos que faltan en el siguiente diagrama.
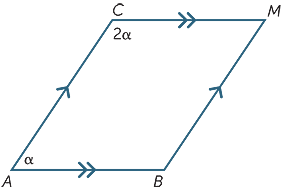
Ejercicio 6
Encontrar el valor de α en el siguiente diagrama.
Declaraciones inversas
Muchas declaraciones en matemáticas tienen una conversación, en la que la implicación va en la dirección opuesta. Por ejemplo, la instrucción
‘ Cada número par termina en 0, 2, 4, 6 u 8.»
tiene converse
» Cada número que termina en 0, 2, 4, 6 u 8 es par.’
Esta declaración en particular y su inversa son ambas verdaderas, pero esto no siempre es
el caso.
Por ejemplo, las siguientes dos sentencias son conversas entre sí:
‘Cada múltiplo de 4 es un número par.’
‘ Cada número par es un múltiplo de 4.’
y aquí, la primera declaración es verdadera, pero la segunda es falsa.
Ejercicio 7
Escriba:
a
una declaración geométrica verdadera cuya inversa es también verdadera,
b declaración geométrica falsa cuya inversa es verdadera,
c una declaración geométrica falsa cuya inversa es también falsa.
Los Teoremas Inversos para Líneas paralelas
Hemos visto que los ángulos correspondientes formados a partir de líneas paralelas son iguales. Podemos escribir la declaración inversa de la siguiente manera. Instrucción
: Si las líneas son paralelas, los ángulos correspondientes son iguales.
Converse: Si los ángulos correspondientes son iguales, entonces las líneas son paralelas.
La instrucción inversa también es verdadera y se usa a menudo para probar que dos líneas son paralelas. Lo mismo es cierto con respecto a los ángulos alternos y co-interiores. Instrucción
: Si las líneas son paralelas, los ángulos alternativos son iguales.
Converse: Si los ángulos alternativos son iguales, entonces las líneas son paralelas.
Declaración: Si las líneas son paralelas, entonces los ángulos co-interiores son suplementarios.
Converse: Si los ángulos co-interiores son suplementarios, entonces las líneas son paralelas.
Así, en cada diagrama, las líneas AB y CD son paralelas.
Ejercicio 8
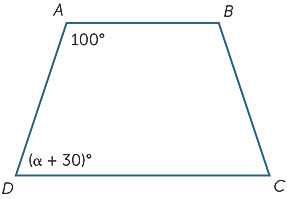¿Qué valor de α hará que AB sea paralelo al CD?
Pruebas de los Tres Conversores
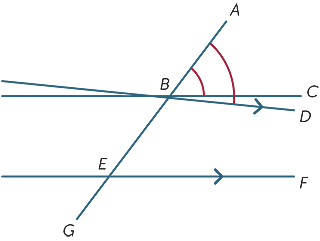Suponemos que los ángulos correspondientes formados por la transversal son iguales y mostramos que las líneas son paralelas.
En el diagrama, suponemos que
ABC = BEF.
Si BC y EF no son paralelos, dibuje
BD paralelo a EF.
Ahora, ya que BD y EF son paralelos ABD = BEF y, por lo tanto, ABC = ABD, lo cual es claramente imposible a menos que las líneas BC y BD sean las mismas. Por lo tanto, las líneas BC y EF son paralelas.
Las otras pruebas siguen de la misma manera.
Ejercicio 9
Dar una prueba del segundo teorema inverso (ángulos alternos).
Suma de ángulos de un triángulo
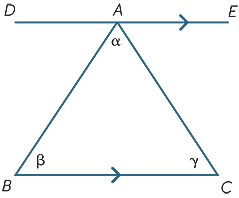Los resultados de la sección anterior se pueden utilizar para deducir uno de los hechos más importantes en geometría: la suma de ángulos de un triángulo es de 180° .
Comenzamos con el triángulo ABC con ángulos α, β, γ como se muestra. Dibuja la línea DAE paralela a BC. Entonces,
DAB = β (ángulos alternos, BC||DE)
EAC = γ (ángulos alternos, BC||DE)
α+ β + γ = 180° (ángulo recto).
Por lo tanto, hemos demostrado el teorema
La suma de los ángulos en un triángulo es de 180°.
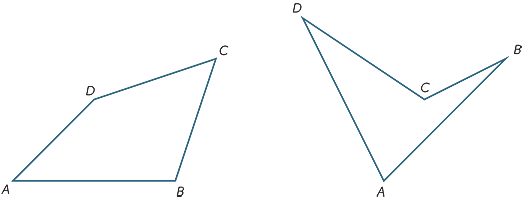
Un cuadrilátero es una figura plana limitada por cuatro lados.
Ejercicio 10
Dividiendo el cuadrilátero ABCD en dos triángulos, encuentre la suma de los ángulos.
El material de este módulo ha comenzado a colocar la geometría sobre una base razonablemente sistemática de objetos cuidadosamente definidos, axiomas que deben asumirse y teoremas que hemos demostrado. Sobre esta base, podemos desarrollar un recuento sistemático de la geometría plana que implica:
- Teorema de Pitágoras
- triángulos congruentes y congruentes
- triángulos similares y similares
- isósceles y triángulos equiláteros
- cuadriláteros especiales, incluidos cuadrados, rectángulos, paralelogramos, rombos y trapecios
- la geometría de los círculos.
La geometría plana también será fundamental en muchas otras áreas de los Años 7-10 matemáticas:
- transformaciones
- geometría tridimensional
- áreas y volúmenes
- trigonometría
- geometría de coordenadas
- los gráficos de círculos y parábolas.
Las ideas de tangentes y áreas conducen a su vez al cálculo en los Años 11-12.
Historia y aplicación
Historia
Las increíbles construcciones de las pirámides y los enormes templos de Egipto revelan que los egipcios deben haber tenido un muy buen conocimiento práctico y comprensión de la geometría básica, al menos a un nivel práctico. Por otro lado, no hay evidencia de que hayan sistematizado ese conocimiento de manera formal. Esto fue dejado a los antiguos griegos. No tenemos conocimiento detallado de esa sistematización, excepto por la afirmación de que Thales(ca. 624 AC-ca. 546 a. C.) dio las primeras «pruebas» de hechos geométricos que marcaron los comienzos de la geometría deductiva. La Escuela Pitagórica continuó este trabajo y Platón (428 a.C. -348 a. C.) se basa claramente en el trabajo de matemáticos anteriores cuando menciona hechos geométricos en sus escritos. Vale la pena leer el diálogo geométrico de su obra el Meno, en la que Sócrates consigue que un niño esclavo llegue a un teorema geométrico mediante una serie de deducciones lógicas. Si los orígenes de la geometría no están claros, el ‘producto final’ no lo está. Euclides (323-283 a.C.), escribiendo en Alejandría, produjo un trabajo notable, llamado los Elementos, que siguió siendo el libro de texto estándar en geometría durante más de 2000 años. En este trabajo, Euclides establece una serie de definiciones (como puntos y líneas), postulados y nociones comunes. (En estos días los llamamos axiomas. A partir de estos, desarrolló lógicamente, en un orden cuidadosamente elegido, un gran número de teoremas que generalmente denominamos Geometría euclidiana. Hay una serie de otros resultados geométricos, como el teorema de Pappus, que se descubrieron después de Euclides, pero generalmente no se cubren en la escuela secundaria.
Uno de los cinco postulados de Euclides no era tan obviamente cierto como los otros parecían serlo. Una versión, conocida como Axioma de Playfair, afirma que: Dada una línea y un punto P, no en , hay una y solo una línea paralela a que pasa por P. En el siglo XIX, varios matemáticos preguntaron: «¿Qué sucede si negamos este postulado?’Esto se hace asumiendo que no hay tal línea paralela, o diciendo que hay más de una línea. Esto llevó al desarrollo de geometrías no euclidianas, una de las cuales ha resultado ser uno de los buenos modelos para el universo.
Aplicaciones
En un sentido muy real, la geometría y la intuición geométrica forman la base de todas las
Matemáticas: la geometría conduce a la geometría de coordenadas que conduce al cálculo y
a todas sus muchas aplicaciones, por lo que es crucial en el plan de estudios.
En un nivel más práctico, los constructores, topógrafos, ingenieros y arquitectos han sido grandes usuarios de la geometría y las ideas geométricas durante siglos. Más recientemente, con el desarrollo de computadoras, artistas gráficos y diseñadores web se han unido a este grupo de personas que necesitan y usan la geometría en su trabajo. Cuando se le preguntó recientemente cuán útil es la geometría, Jim Kelly, un científico aplicado, dijo :.. la geometría es una parte importante del diseño, el dibujo y el modelado por computadora. También se utiliza con frecuencia en … cursos de física y otras ciencias físicas como parte de la comprensión de los efectos de las cargas en estructuras y puntos de equilibrio(centros de gravedad) para sólidos compuestos. En química, la comprensión de la geometría de una molécula está relacionada con la comprensión de las propiedades de las sustancias. Existen muchos más ejemplos. (del sitio web Ask a Scientist.)
Una historia de las Matemáticas: Introducción, 3a Edición, Victor J. Katz, Addison-Wesley, (2008)
Historia de las Matemáticas, D. E. Smith, Dover publications Nueva York, (1958)
RESPUESTAS A EJERCICIOS
EJERCICIO 1
EJERCICIO 2
Los puntos son colineales
EJERCICIO 3
60°
EJERCICIO 4
DBA = 102° (ángulos correspondientes, AB / / CD)
BAC = 78° (co-ángulos interiores, AC||BD)
EJERCICIO 5
α = 65°
(ángulos correspondientes, AC||BM)
β = 80° (ángulos alternativos, AC||BM)
γ + β = 115° (co-ángulos interiores, AC||BM)
Por lo tanto, γ = 35°
(Esta es la estructura para una prueba del resultado de que la suma de ángulos de un triángulo es 180°)
EJERCICIO 6
α = 60 °
EJERCICIO 7
a Un cuadrilátero con cada uno de sus ángulos interiores un ángulo recto es un rectángulo.
Converse: Cada ángulo interior de un rectángulo es un ángulo recto.
b Un rectángulo es un cuadrado
Converse: Un cuadrado es un rectángulo
cLa suma de los ángulos interiores de un triángulo es de 200°
Converse: Un polígono para el que la suma del ángulo interior es de 200° es un triángulo.
EJERCICIO 8
α = 50°
EJERCICIO 9
Nos referimos a el mismo diagrama.
Coloque un punto H en la línea EF a la izquierda de E.
CBE = BEH
Si BC y EF no son paralelos, dibuje BD paralelo a EF.
Dado que BD y EF son paralelos, EBD= BEH, lo cual es claramente imposible a menos que las líneas BC y BD sean las mismas.
Por lo tanto, las líneas BC y EF son paralelas.
EJERCICIO 10
360°
El Proyecto para Mejorar la Educación Matemática en las Escuelas (TIMES) 2009-2011 fue financiado por el Departamento de Educación, Empleo y Relaciones Laborales del Gobierno australiano.
Las opiniones expresadas aquí son las del autor y no representan necesariamente las opiniones del Departamento de Educación, Empleo y Relaciones Laborales del Gobierno de Australia.
© La Universidad de Melbourne en nombre del Centro Internacional de Excelencia para la Educación en Matemáticas (ICE-EM), la división de educación del Instituto Australiano de Ciencias Matemáticas (AMSI), 2010 (excepto donde se indique lo contrario). Esta obra está bajo la Licencia Creative Commons Atribución-NoComercial-SinDerivadas 3.0 Unported.
https://creativecommons.org/licenses/by-nc-nd/3.0/
