Hoy será una breve introducción a las estadísticas circulares (a veces denominadas estadísticas direccionales). La estadística circular es una subdivisión interesante de estadísticas que involucra observaciones tomadas como vectores alrededor de un círculo unitario. Por ejemplo, imagine medir los tiempos de nacimiento en un hospital durante un ciclo de 24 horas, o la dispersión direccional de un grupo de animales migratorios. Este tipo de datos está involucrado en una variedad de campos, como la ecología, la climatología y la bioquímica. La naturaleza de las observaciones de medición alrededor de un círculo unitario requiere un enfoque diferente para la prueba de hipótesis. Las distribuciones deben estar «envueltas» alrededor del círculo para ser útiles, y los estimadores convencionales, como la media de la muestra o la varianza de la muestra, no retienen agua.
En esta publicación, realizaremos la prueba de espaciado de Rao para evaluar la uniformidad de un conjunto de datos circular. Este es un procedimiento básico y debe considerarse como una introducción al manejo de datos circulares.
Primeros pasos
Vamos a realizar una prueba de hipótesis en tortugas, un pequeño conjunto de datos que consta de los ángulos de llegada de 10 tortugas marinas verdes a su isla de anidación. Nuestro objetivo es determinar dónde los ángulos de llegada muestran signos de direccionalidad o son más indicativos de una dispersión aleatoria.
Primero, instale el paquete circular y adjunte el conjunto de datos turtles.
install.packages("circular")require(circular)attach(turtles)
Trazado de los datos
El paquete circular contiene su propia función de trazado, plot.circular. Observemos los ángulos de llegada de las tortugas.
plot.circular(arrival)
Aquí está la trama: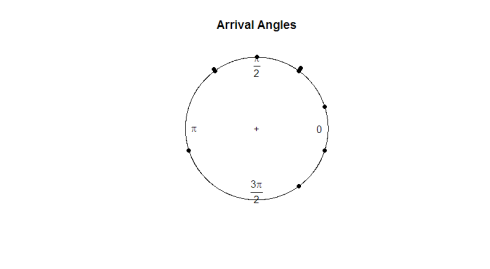
Dada la prueba ocular, las observaciones parecen ser uniformes alrededor del círculo. Si queremos ejecutar una prueba de hipótesis para determinar si los datos son realmente uniformes, necesitaremos desarrollar una estadística de prueba que funcione con datos angulares.
¿Cuál es un buen parámetro que podemos utilizar? Tomar la media de la muestra no nos dice mucho sobre la dirección de los datos (180 grados no es una media útil de 2 grados y 358 grados). En la siguiente gráfica, observe cómo la media de la muestra no sirve para representar la forma o la extensión de nuestros datos.
mean(arrival)plot.circular(mean(arrival)) 0.9120794
Aquí está la trama: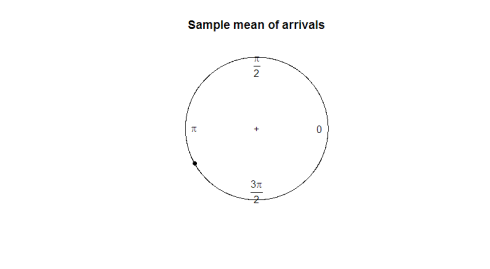
En su lugar, usaremos un método que determina la direccionalidad midiendo el espacio promedio entre observaciones. Esta prueba se llama Prueba de Espaciado de Rao.
Prueba de Espaciado de Rao
La Prueba de Espaciado de Rao se desarrolló para evaluar la uniformidad de los datos circulares. Utiliza el espacio entre observaciones para determinar si los datos muestran una direccionalidad significativa. Si los datos son uniformes, las observaciones deben tender a estar separadas uniformemente.
Aquí está la estadística de prueba \(U\) para la prueba de espaciado de Rao: $ $U = 1/2 \ sum\limits_{i=1} ^ n / T_ {i} – λ / where donde \ (λ = 360 / n, T_ {i} = f_ {i + 1}-f_{i}\) y \ (T_ {n} = (360-f_ {n})+f_{1}\)
Básicamente, el estadístico de prueba agrega las desviaciones entre puntos consecutivos, cada uno ponderado por el número total de observaciones en el conjunto de datos.
Usaremos la función rao.spacing.test() para ejecutar esta prueba de hipótesis. Nuestra hipótesis nula dice que los datos son de una distribución uniforme, mientras que la alternativa establece que los datos muestran signos de direccionalidad. Hagamos la prueba.
rao.spacing.test(arrival,alpha=.10) Rao's Spacing Test of Uniformity Test Statistic = 127.2689 Level 0.1 critical value = 161.23 Do not reject null hypothesis of uniformity
Con una estadística de prueba de 127 que cae por debajo del valor crítico de 161, los datos no se inclinan significativamente en ninguna dirección. No podemos rechazar la hipótesis de que las llegadas de tortugas son de distribución uniforme.
Conclusión
La prueba de espaciado de Rao determinó que los datos no mostraban signos de tendencias direccionales. No podemos rechazar la hipótesis nula de uniformidad y asumiremos uniformidad con respecto a la dirección de llegada. Si bien esta publicación fue un tutorial relativamente básico, muchas personas en la comunidad de ciencia de datos no han trabajado con datos circulares antes. Es un sub-tema interesante en el que sumergirse, así como un campo joven de la estadística que aún está evolucionando.
Observaciones finales
Me gustaría extender el crédito a S. Rao Jammalamadaka PhD, de la Universidad de California, Santa Bárbara, y su libro de texto «Temas en Estadísticas Circulares» por despertar mi interés en el campo de las estadísticas circulares.