Según Noam Chomosky, hay cuatro tipos de gramáticas de Tipo 0, tipo 1, Tipo 2 y Tipo 3. La siguiente tabla muestra cómo se diferencian unos de otros−
| la Gramática de Tipo | Gramática Aceptado | Idioma Aceptado | Autómata |
|---|---|---|---|
| Tipo 0 | sin restricciones de la gramática | Recursivamente enumerable idioma | Máquina de Turing |
| Tipo 1 | sensible al Contexto de la gramática | Contextual del lenguaje | Lineal acotado autómata |
| Tipo 2 | gramática independiente del Contexto | Contexto de un lenguaje libre | Pushdown autómata |
| Tipo 3 | Regular la gramática | lenguaje Regular | autómata de estado Finito |
echa un vistazo a la siguiente ilustración. Muestra el alcance de cada tipo de gramática −
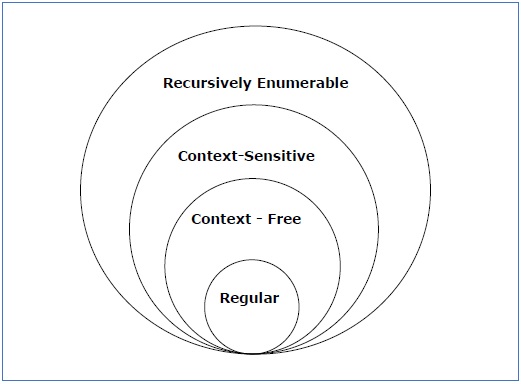
Gramática de Tipo 3
Las gramáticas de tipo 3 generan idiomas regulares. Tipo 3 gramáticas debe tener una sola no-terminal en el lado izquierdo y un lado derecho que consta de una sola terminal o terminal seguido de un no terminal.
Las producciones deben estar en la forma X → a o X → aY
donde X, Y ∈ N (No terminal)
y a ∈ T (Terminal)
Se permite la regla S → ε si S no aparece en el lado derecho de ninguna regla.
Ejemplo
X → ε X → a | aYY → b
Gramática de tipo 2
Las gramáticas de tipo 2 generan lenguajes sin contexto.
Las producciones deben ser de la forma a → γ
donde a ∈ N (No terminal)
y γ ∈ (T ∪ N)* (Cadena de terminales y no terminales).
Estos lenguajes generados por estas gramáticas son reconocidos por un autómata de empuje no determinista.
Ejemplo
S → X a X → a X → aX X → abc X → ε
Gramática de tipo 1
Las gramáticas de tipo 1 generan lenguajes sensibles al contexto. Las producciones deben estar en la forma
α A β → α γ β
donde A ∈ N (No terminal)
y α, β, γ ∈ (T N N)* (Cadenas de terminales y no terminales)
Las cadenas α y β pueden estar vacías, pero γ no debe estar vacía.
Se permite la regla S → ε si S no aparece en el lado derecho de ninguna regla. Las lenguas generadas por estas gramáticas son reconocidas por un autómata acotado lineal.
Ejemplo
AB → AbBc A → bcA B → b
Gramática de tipo 0
Las gramáticas de tipo 0 generan lenguajes enumerables recursivamente. Las producciones no tienen restricciones. Son cualquier gramática de estructura de fase, incluidas todas las gramáticas formales.
Generan los lenguajes que son reconocidos por una máquina de Turing.
Las producciones pueden ser en forma de α → β donde α es una cadena de terminales y no terminales con al menos una no terminal y α no puede ser nula. β es una cadena de terminales y no terminales.
Ejemplo
S → ACaB Bc → acB CB → DB aD → Db