El catamorfismo de Cualquiera de los Dos es una generalización de su pliegue. El catamorfismo permite operaciones no disponibles a través de pliegue.
Este artículo es parte de una serie de artículos sobre catamorfismos. Un catamorfismo es una abstracción universal que describe cómo digerir una estructura de datos en un valor potencialmente más compacto.
Este artículo presenta el catamorfismo para Cualquiera de los Dos (también conocido como Resultado), así como la forma de identificarlo. El comienzo de este artículo presenta el catamorfismo en C#, con ejemplos. El resto del artículo describe cómo deducir el catamorfismo. Esta parte del artículo presenta mi trabajo en Haskell. Los lectores que no se sientan cómodos con Haskell pueden leer la primera parte y considerar el resto del artículo como un apéndice opcional.
O bien es un contenedor de datos que modela dos resultados mutuamente excluyentes. A menudo se usa para devolver valores que pueden ser correctos (derecha) o incorrectos (izquierda). En la programación funcional de tipo estático con preferencia por funciones totales, cualquiera de los dos ofrece una forma más sana y razonable de modelar resultados de éxito y error que lanzar excepciones.
C # catamorphism #
Este artículo utiliza la codificación de la Iglesia de Cualquiera de los Dos. El catamorfismo para Cualquiera de los dos es el método Match :
T Match<T>(Func<L, T> onLeft, Func<R, T> onRight);
Hasta este artículo, todos los catamorfismos anteriores han sido un par hecho de un valor inicial y una función. El catamorfismo es una generalización, ya que es un par de funciones. Una función maneja el caso donde hay un valor a la izquierda, y la otra función maneja el caso donde hay un valor a la derecha. Ambas funciones deben devolver el mismo tipo unificador, que a menudo es una cadena o algo similar que se puede mostrar en una interfaz de usuario:
> IEither<TimeSpan, int> e = new Left<TimeSpan, int>(TimeSpan.FromMinutes(3));> e.Match(ts => ts.ToString(), i => i.ToString())"00:03:00"> IEither<TimeSpan, int> e = new Right<TimeSpan, int>(42);> e.Match(ts => ts.ToString(), i => i.ToString())"42"
A menudo verá ejemplos como el anterior que convierte los casos izquierdo y derecho en cadenas o algo que se puede representar como un tipo de respuesta unificadora, pero esto no es necesario de ninguna manera. Si puede crear un tipo unificador, puede convertir ambos casos a ese tipo:
> IEither<Guid, string> e = new Left<Guid, string>(Guid.NewGuid());> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)12> IEither<Guid, string> e = new Right<Guid, string>("foo");> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)3
En los dos ejemplos anteriores, se utilizan dos funciones diferentes que reducen los valores Guid y string respectivamente a un número. La función que convierte valores Guid en un número cuenta cuántos dígitos hexadecimales son mayores o iguales a A (10). La otra función simplemente devuelve la longitud de string, si está allí. Ese ejemplo tiene poco sentido, pero al método Match no le importa eso.
En la práctica, Cualquiera de los dos se utiliza a menudo para el manejo de errores. El artículo sobre la codificación de la Iglesia de Cualquiera de los Dos contiene un ejemplo.
Ya sea Álgebra F #
Como en el artículo anterior, usaré Fix y cata como se explica en el excelente artículo de Bartosz Milewski sobre Álgebras F.
Mientras que las álgebras F y los puntos fijos se utilizan principalmente para estructuras de datos recursivas, también puede definir un Álgebra F para una estructura de datos no recursiva. Ya viste un ejemplo de eso en los artículos sobre catamorfismo booleano y Tal vez catamorfismo. La diferencia entre, por ejemplo, valores Maybe y Cualquiera de los dos es que ambos casos de Cualquiera de los dos tienen un valor. Puede modelar esto como Functor con un tipo de portador y dos argumentos de tipo para los datos que pueden contener:
data EitherF l r c = LeftF l | RightF r deriving (Show, Eq, Read) instance Functor (EitherF l r) where fmap _ (LeftF l) = LeftF l fmap _ (RightF r) = RightF r
Elegí llamar a los’ tipos de datos ‘ l (para izquierda) y r (para derecha), y al tipo de operador c (para operador). Como también fue el caso con BoolF y MaybeF, la instancia Functor ignora la función de mapa porque falta el tipo de portador tanto en el caso LeftF como en el caso RightF. Al igual que las instancias Functor para BoolF y MaybeF, parecería que no pasa nada, pero a nivel de tipo, esto sigue siendo una traducción de EitherF l r c a EitherF l r c1. No es una gran función, tal vez, pero definitivamente un endofuntor.
Como también fue el caso al deducir los catamorfismos Maybe y List, Haskell no está muy contento con definir instancias para un tipo como Fix (EitherF l r). Para resolver ese problema, puede introducir un envoltorio newtype :
newtype EitherFix l r = EitherFix { unEitherFix :: Fix (EitherF l r) } deriving (Show, Eq, Read)
Puede definir Functor, Applicative, Monad, etc. instancias para este tipo sin recurrir a extensiones GHC funky. Tenga en cuenta que, en última instancia, el propósito de todo este código es averiguar cómo se ve el catamorfismo. Este código no está pensado para su uso real.
Un par de funciones auxiliares facilitan la definición de valores EitherFix :
leftF :: l -> EitherFix l rleftF = EitherFix . Fix . LeftF rightF :: r -> EitherFix l rrightF = EitherFix . Fix . RightF
Con esas funciones, puede crear valores EitherFix :
Prelude Data.UUID Data.UUID.V4 Fix Either> leftF <$> nextRandomEitherFix {unEitherFix = Fix (LeftF e65378c2-0d6e-47e0-8bcb-7cc29d185fad)}Prelude Data.UUID Data.UUID.V4 Fix Either> rightF "foo"EitherFix {unEitherFix = Fix (RightF "foo")}
Eso es todo lo que necesitas para identificar el catamorfismo.
Catamorfismo de Haskell #
En este punto, tienes dos de tres elementos de un Álgebra F. Tiene un endofunctor (EitherF l r) y un objeto c, pero aún necesita encontrar un morfismo EitherF l r c -> c. Observe que el álgebra que tiene que encontrar es la función que reduce el funtor a su tipo portador c, no los ‘tipos de datos’ l y r. Esto lleva algún tiempo acostumbrarse, pero así es como funcionan los catamorfismos. Sin embargo, esto no significa que puedas ignorar l y r, como verás.
Como en los artículos anteriores, comience escribiendo una función que se convertirá en el catamorfismo, basado en cata:
eitherF = cata alg . unEitherFix where alg (LeftF l) = undefined alg (RightF r) = undefined
Aunque compila, con sus implementaciones undefined, obviamente no hace nada útil. Me parece, sin embargo, que me ayuda a pensar. ¿Cómo puede devolver un valor del tipo c del caso LeftF? Puede pasar un argumento a la función eitherF :
eitherF fl = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = undefined
Aunque, técnicamente, podría pasar un argumento del tipo c a eitherF y luego devolver ese valor desde el caso LeftF, eso significaría que ignoraría el valor l. Esto sería incorrecto, así que en su lugar, convierta el argumento en una función y llámelo con l. Del mismo modo, puede tratar el caso RightF de la misma manera:
eitherF :: (l -> c) -> (r -> c) -> EitherFix l r -> ceitherF fl fr = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = fr r
Esto funciona. Dado que cata tiene el tipo Functor f => (f a -> a) -> Fix f -> a, eso significa que alg tiene el tipo f a -> a. En el caso de EitherF, el compilador infiere que la función alg tiene el tipo EitherF l r c -> c, ¡que es justo lo que necesita!
Ahora puede ver para qué sirve el tipo de portador c. Es el tipo que extrae el álgebra, y por lo tanto el tipo que devuelve el catamorfismo.
Este, entonces, es el catamorfismo para Cualquiera de los Dos. Como ha sido consistente hasta ahora, es un par, pero ahora está hecho de dos funciones. Como ha visto en repetidas ocasiones, este no es el único catamorfismo posible, ya que puede, por ejemplo, voltear trivialmente los argumentos a eitherF.
He elegido la representación que se muestra aquí porque es isomórfica a la función either del módulo Data.Either incorporado de Haskell, que llama a la función «Análisis de casos para el tipo Either«. Ambas funciones (eitherF y either) son equivalentes al método anterior de C# Match.
Basis #
Puede implementar la mayoría de las otras funcionalidades útiles con eitherF. Aquí está la instancia Bifunctor :
instance Bifunctor EitherFix where bimap f s = eitherF (leftF . f) (rightF . s)
A partir de esa instancia, la instancia Functor sigue trivialmente:
instance Functor (EitherFix l) where fmap = second
En la parte superior de Functor puede agregar Applicative:
instance Applicative (EitherFix l) where pure = rightF f <*> x = eitherF leftF (<$> x) f
Observe que la implementación <*> es similar a la implementación <*> para MaybeFix. Lo mismo ocurre con la instancia Monad :
instance Monad (EitherFix l) where x >>= f = eitherF leftF f x
No solo es EitherFix Foldable, es Bifoldable:
instance Bifoldable EitherFix where bifoldMap = eitherF
Observe, curiosamente, que bifoldMap es idéntico a eitherF.
La instancia Bifoldable le permite implementar trivialmente la instancia Foldable :
instance Foldable (EitherFix l) where foldMap = bifoldMap mempty
Puede encontrar la presencia de mempty desconcertante, ya que bifoldMap (o eitherF; son idénticos) toma como argumentos dos funciones. Es mempty una función?
Sí mempty puede ser una función. Aquí está. Hay una instancia Monoid para cualquier función a -> m, donde m es una instancia Monoid, y mempty es la identidad para ese monoide. Esa es la instancia en uso aquí.
Así como EitherFix es Bifoldable, también es Bitraversable:
instance Bitraversable EitherFix where bitraverse fl fr = eitherF (fmap leftF . fl) (fmap rightF . fr)
Puede implementar cómodamente la instancia Traversable en función de la instancia Bitraversable :
instance Traversable (EitherFix l) where sequenceA = bisequenceA . first pure
Finalmente, puede implementar conversiones hacia y desde el tipo Either estándar, utilizando ana como el dual de cata:
toEither :: EitherFix l r -> Either l rtoEither = eitherF Left Right fromEither :: Either a b -> EitherFix a bfromEither = EitherFix . ana coalg where coalg (Left l) = LeftF l coalg (Right r) = RightF r
Esto demuestra que EitherFix es isomorfo a Either, lo que de nuevo establece que eitherF y either son equivalentes.
Relaciones #
En esta serie, has visto varios ejemplos de catamorfismos de estructuras que no tienen pliegues, catamorfismos que coinciden con pliegues, y ahora un catamorfismo que es más general que el pliegue. La introducción a la serie incluía este diagrama:
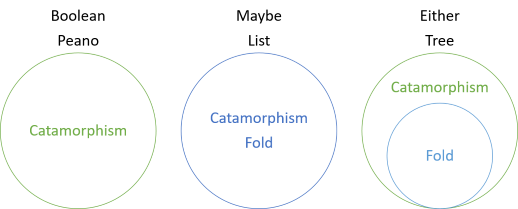
Esto muestra que los valores booleanos y los números de Peano tienen catamorfismos, pero no pliegues, mientras que para Maybe y List, el pliegue y el catamorfismo son los mismos. Para cualquiera, sin embargo, el pliegue es un caso especial del catamorfismo. El pliegue de cualquiera de los dos «pretende» que el lado izquierdo no existe. En su lugar, el valor de la izquierda se interpreta como un valor de la derecha que falta. Por lo tanto, para plegar cualquiera de los valores, debe proporcionar un valor de ‘reserva’ que se utilizará en caso de que uno de los valores no sea un valor correcto:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e""
En una sesión GHCi como la anterior, puede crear dos valores del mismo tipo. El caso derecho es un valor Ordering, mientras que el caso izquierdo es un valor Integer.
Con foldr, no hay forma de acceder al estuche izquierdo. Si bien puede acceder y transformar el valor Ordering correcto, el número 42 simplemente se ignora durante el pliegue. En su lugar, se devuelve el valor predeterminado "".
Contrasta esto con el catamorfismo, que puede acceder a ambos casos:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"42"
En una sesión como esta, se recrean los mismos valores, pero con el catamorfismo eitherF, ahora se puede acceder y transformar los casos izquierdo y derecho. En otras palabras, el catamorfismo le permite realizar operaciones que no son posibles con el pliegue.
Es interesante, sin embargo, notar que mientras el pliegue es una especialización del catamorfismo, el bifold es idéntico al catamorfismo.
Resumen #
El catamorfismo para Cualquiera de los dos es un par de funciones. Una función transforma la caja izquierda, mientras que la otra función transforma la caja derecha. Para cualquier valor, solo se utilizará una de esas funciones.
Cuando originalmente me encontré con el concepto de catamorfismo, me resultó difícil distinguir entre catamorfismo y pliegue. Mi problema fue, creo, que los tutoriales con los que me encontré en su mayoría usaban listas enlazadas para demostrar cómo, en ese caso, el pliegue es el catamorfismo. Resulta, sin embargo, que este no siempre es el caso. Un catamorfismo es una abstracción general. Un pliegue, por otro lado, me parece que está relacionado principalmente con colecciones.
En este artículo viste el primer ejemplo de un catamorfismo que puede hacer más que el pliegue. Para cualquiera de los dos, el pliegue es solo un caso especial del catamorfismo. También viste, sin embargo, cómo el catamorfismo era idéntico al bifold. Por lo tanto, todavía no está del todo claro cómo se relacionan estos conceptos. Por lo tanto, en el siguiente artículo, obtendrás un ejemplo de un contenedor donde no hay bifold, y donde el catamorfismo es, de hecho, una generalización del pliegue.
Siguiente: Catamorfismo de árbol.