Evaluación | Biopsicología | Comparativa |Cognitiva | de Desarrollo | Lenguaje | Diferencias individuales |Personalidad | Filosofía | Social |
Métodos | Estadística |Artículos Clínicos | Educativos | Industriales |Profesionales |Psicología mundial |
Estadística:Método científico · Métodos de investigación · Diseño experimental · Cursos de estadística de pregrado · Pruebas estadísticas · Teoría de juegos · Teoría de decisiones
Por favor, ayuda a mejorar esta página tú mismo si puedes..
El análisis de clústeres es una técnica común para el análisis de datos estadísticos, que se utiliza en muchos campos, incluido el aprendizaje automático, la minería de datos, el reconocimiento de patrones, el análisis de imágenes y la bioinformática. La agrupación en clústeres es la clasificación de objetos similares en grupos diferentes, o más precisamente, la partición de un conjunto de datos en subconjuntos (clústeres), de modo que los datos de cada subconjunto (idealmente) compartan algún rasgo común, a menudo proximidad de acuerdo con alguna medida de distancia definida.
Además del término agrupación de datos (o simplemente agrupación), hay varios términos con significados similares, incluyendo análisis de clústeres, clasificación automática, taxonomía numérica, botryología y análisis tipológico.
- Tipos de clústeres
- Agrupamiento jerárquico
- Medida de distancia
- Creación de clústeres
- Agrupamiento jerárquico aglomerativo
- Agrupamiento particional
- k-medias y derivadas
- Agrupamiento de K-medias
- Algoritmo de Clust de QT
- C difusa-significa agrupación
- Criterio de codo
- Agrupación espectral
- Aplicaciones
- Biología
- Investigación de mercado
- Otras aplicaciones
- Comparaciones entre agrupamientos de datos
- Véase también
- Bibliografía
- Implementaciones de software
- Gratuito
Tipos de clústeres
Los algoritmos de clústeres de datos pueden ser jerárquicos o particionales. Los algoritmos jerárquicos encuentran clústeres sucesivos utilizando clústeres previamente establecidos, mientras que los algoritmos particionales determinan todos los clústeres a la vez. Los algoritmos jerárquicos pueden ser aglomerativos (de abajo hacia arriba) o divisivos (de arriba hacia abajo). Los algoritmos aglomerativos comienzan con cada elemento como un grupo separado y los fusionan en grupos sucesivamente más grandes. Los algoritmos divisivos comienzan con todo el conjunto y proceden a dividirlo en grupos sucesivamente más pequeños.
Agrupamiento jerárquico
Medida de distancia
Un paso clave en un agrupamiento jerárquico es seleccionar una medida de distancia. Una medida simple es la distancia de Manhattan, igual a la suma de distancias absolutas para cada variable. El nombre proviene del hecho de que en un caso de dos variables, las variables se pueden trazar en una cuadrícula que se puede comparar con las calles de la ciudad, y la distancia entre dos puntos es el número de bloques que una persona caminaría.
Una medida más común es la distancia euclidiana, calculada encontrando el cuadrado de la distancia entre cada variable, sumando los cuadrados y encontrando la raíz cuadrada de esa suma. En el caso de dos variables, la distancia es análoga a encontrar la longitud de la hipotenusa en un triángulo; es decir, es la distancia «en línea recta».»Una revisión del análisis de conglomerados en investigaciones de psicología de la salud encontró que la medida de distancia más común en estudios publicados en esa área de investigación es la distancia euclidiana o la distancia euclidiana cuadrada.
Creación de clústeres
Dada una medida de distancia, los elementos se pueden combinar. La agrupación jerárquica construye (aglomerativa), o se rompe (divisiva), una jerarquía de clústeres. La representación tradicional de esta jerarquía es una estructura de datos de árbol (llamada dendrograma), con elementos individuales en un extremo y un solo clúster con cada elemento en el otro. Los algoritmos aglomerativos comienzan en la parte superior del árbol, mientras que los algoritmos divisivos comienzan en la parte inferior. (En la figura, las flechas indican un agrupamiento aglomerativo.)
Cortar el árbol a una altura determinada dará un agrupamiento con una precisión seleccionada. En el siguiente ejemplo, el corte después de la segunda fila producirá racimos {a} {b c} {d e} {f}. El corte después de la tercera fila producirá clústeres {a} {b c} {d e f}, que es una agrupación más gruesa, con un número menor de clústeres más grandes.
Agrupamiento jerárquico aglomerativo
Por ejemplo, supongamos que estos datos se agrupan. Donde la distancia euclidiana es la métrica de distancia.
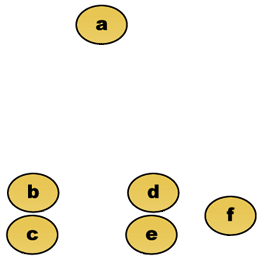
Datos brutos
El dendrograma de agrupamiento jerárquico sería como tal:
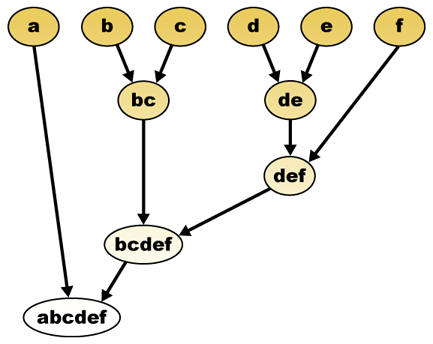
Representación tradicional
Este método construye la jerarquía a partir de los elementos individuales fusionando progresivamente los clústeres. De nuevo, tenemos seis elementos {a} {b} {c} {d} {e} y {f}. El primer paso es determinar qué elementos combinar en un clúster. Por lo general, queremos tomar los dos elementos más cercanos, por lo tanto, debemos definir una distancia 
Supongamos que hemos fusionado los dos elementos más cercanos b y c, ahora tenemos los siguientes clústeres {a}, {b, c}, {d}, {e} y {f}, y queremos fusionarlos aún más. Pero para hacer eso, necesitamos tomar la distancia entre {a} y {b c}, y por lo tanto definir la distancia entre dos grupos. Por lo general, la distancia entre dos grupos 
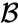
- La distancia máxima entre los elementos de cada clúster (también llamada agrupación de enlace completo):
- La distancia mínima entre los elementos de cada clúster (también llamada agrupación de enlace único):
- La distancia media entre los elementos de cada clúster(también llamada agrupación de enlace promedio):
- La suma de toda la varianza dentro del clúster
- El aumento de la varianza para el clúster que se fusiona (criterio de Ward)
- La probabilidad de que los clústeres candidatos aparezcan a partir de la misma función de distribución (V-linkage)
Cada aglomeración se produce a una distancia mayor entre los clústeres que la aglomeración anterior, y uno puede decidir detener la agrupación cuando los clústeres están demasiado separados para ser fusionados (criterio de distancia) o cuando hay un número suficientemente pequeño de clústeres (criterio de número).
Agrupamiento particional
k-medias y derivadas
Agrupamiento de K-medias
El algoritmo de K-medias asigna cada punto al clúster cuyo centro (también llamado centroide) es el más cercano. El centro es el promedio de todos los puntos del clúster, es decir, sus coordenadas son la media aritmética para cada dimensión por separado sobre todos los puntos del clúster.
Ejemplo: El conjunto de datos tiene tres dimensiones y el clúster tiene dos puntos: X = (x1, x2, x3) e Y = (y1, y2, y3). Entonces el centroide Z se convierte en Z = (z1, z2, z3), donde z1 = (x1 + y1)/2 y z2 = (x2 + y2)/2 y z3 = (x3 + y3)/2.
El algoritmo es más o menos (J. MacQueen, 1967):
- Genere aleatoriamente k clústeres y determine los centros de clústeres, o genere directamente k puntos de semilla como centros de clústeres.
- Asigne cada punto al centro de clúster más cercano.
- Vuelva a calcular los nuevos centros de clúster.
- Repetir hasta que se cumpla algún criterio de convergencia (generalmente que la asignación no ha cambiado).
Las principales ventajas de este algoritmo son su simplicidad y velocidad, lo que le permite ejecutarse en grandes conjuntos de datos. Su desventaja es que no produce el mismo resultado con cada ejecución, ya que los clústeres resultantes dependen de las asignaciones aleatorias iniciales. Maximiza la varianza entre clústeres (o minimiza la varianza intraclústeres), pero no garantiza que el resultado tenga un mínimo global de varianza.
Algoritmo de Clust de QT
El agrupamiento de QT (Umbral de calidad) (Heyer et al, 1999) es un método alternativo de partición de datos, inventado para el agrupamiento de genes. Requiere más potencia de cálculo que k-means, pero no requiere especificar el número de clústeres a priori, y siempre devuelve el mismo resultado cuando se ejecuta varias veces.
El algoritmo es:
- El usuario elige un diámetro máximo para los clústeres.
- Cree un clúster candidato para cada punto incluyendo el punto más cercano, el siguiente más cercano, etc., hasta que el diámetro del clúster supere el umbral.
- Guarde el clúster candidato con la mayor cantidad de puntos como el primer clúster verdadero y elimine todos los puntos del clúster de una consideración posterior.
- Recurse con el conjunto reducido de puntos.
La distancia entre un punto y un grupo de puntos se calcula utilizando completa de ligamiento, es decir, como la distancia máxima desde el punto hasta cualquier miembro del grupo (consulte la sección «Agrupamiento jerárquico aglomerativo» sobre la distancia entre los grupos).
C difusa-significa agrupación
En la agrupación difusa, cada punto tiene un grado de pertenencia a grupos, como en la lógica difusa, en lugar de pertenecer completamente a un solo grupo. Por lo tanto, los puntos en el borde de un clúster, pueden estar en el clúster en menor grado que los puntos en el centro del clúster. Para cada punto x tenemos un coeficiente que da el grado de estar en el cúmulo k 

Con medias c difusas, el centroide de un clúster es la media de todos los puntos, ponderada por su grado de pertenencia al clúster:
El grado de pertenencia está relacionado con el inverso de la distancia al clúster
luego, los coeficientes se normalizan y se difuminan con un parámetro real 
Para m igual a 2, esto es equivalente a normalizar el coeficiente linealmente para hacer su suma 1. Cuando m está cerca de 1, el centro del clúster más cercano al punto recibe mucho más peso que los demás, y el algoritmo es similar a k-means.
El algoritmo de medias c difusas es muy similar al algoritmo de medias k:
- Elija un número de clústeres.
- Asigne aleatoriamente a cada punto coeficientes para estar en los clústeres.
- Repetir hasta que el algoritmo haya convergido (es decir, el cambio de coeficientes entre dos iteraciones no es superior a
, el umbral de sensibilidad dado) :
- Calcule el centroide para cada clúster, utilizando la fórmula anterior.
- Para cada punto, calcule sus coeficientes de estar en los clústeres, utilizando la fórmula anterior.
El algoritmo también minimiza la varianza intra-clúster, pero tiene los mismos problemas que las medias k, el mínimo es un mínimo local y los resultados dependen de la elección inicial de pesos.
Criterio de codo
El criterio de codo es una regla empírica común para determinar el número de grupos que se deben elegir, por ejemplo, para las medias k y la agrupación jerárquica aglomerativa.
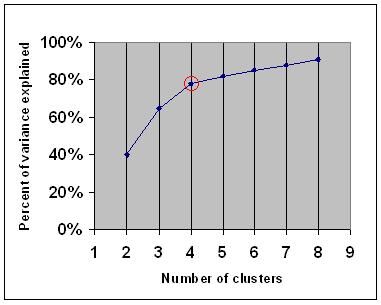
El criterio de codo dice que debe elegir un número de clústeres para que agregar otro clúster no agregue suficiente información. Más precisamente, si graficas el porcentaje de varianza explicado por los clústeres contra el número de clústeres, los primeros clústeres agregarán mucha información (explicarán mucha varianza), pero en algún momento la ganancia marginal caerá, dando un ángulo en el gráfico (el codo).
En el siguiente gráfico, el codo está indicado por el círculo rojo. Por lo tanto, el número de agrupaciones elegidas debe ser de 4.
Agrupación espectral
Dado un conjunto de puntos de datos, la matriz de similitud puede definirse como una matriz 


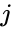
Una de estas técnicas es el algoritmo Shi-Malik, comúnmente utilizado para la segmentación de imágenes. Divide los puntos en dos conjuntos 

de 
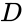
Esta partición se puede hacer de varias maneras, como tomar la mediana 



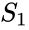
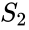
Un algoritmo relacionado es el algoritmo Meila-Shi, que toma los vectores propios correspondientes a los valores propios más grandes de k de la matriz 
Aplicaciones
Biología
En biología, la agrupación en clústeres tiene muchas aplicaciones en los campos de la biología computacional y la bioinformática, dos de las cuales son:
- En transcriptómica, la agrupación se utiliza para construir grupos de genes con patrones de expresión relacionados. A menudo, estos grupos contienen proteínas funcionalmente relacionadas, como enzimas para una vía específica, o genes que están corregulados. Los experimentos de alto rendimiento que utilizan etiquetas de secuencia expresada (EST) o microarrays de ADN pueden ser una herramienta poderosa para la anotación del genoma, un aspecto general de la genómica.
- En el análisis de secuencias, la agrupación se utiliza para agrupar secuencias homólogas en familias de genes. Este es un concepto muy importante en bioinformática y en biología evolutiva en general. Véase evolución por duplicación de genes.
Investigación de mercado
El análisis de clústeres se utiliza ampliamente en la investigación de mercado cuando se trabaja con datos multivariantes de encuestas y paneles de prueba. Los investigadores de mercado utilizan el análisis de conglomerados para dividir la población general de consumidores en segmentos de mercado y comprender mejor las relaciones entre los diferentes grupos de consumidores/clientes potenciales.
- Segmentar el mercado y determinar los mercados objetivo
- Posicionamiento de productos
- Desarrollo de nuevos productos
- Seleccionar mercados de prueba (ver : técnicas experimentales)
Otras aplicaciones
Análisis de redes sociales: En el estudio de las redes sociales, la agrupación puede usarse para reconocer comunidades dentro de grupos grandes de personas.
Segmentación de imágenes: La agrupación en clústeres se puede utilizar para dividir una imagen digital en regiones distintas para la detección de bordes o el reconocimiento de objetos.
Minería de datos: Muchas aplicaciones de minería de datos implican la partición de elementos de datos en subconjuntos relacionados; las aplicaciones de marketing mencionadas anteriormente representan algunos ejemplos. Otra aplicación común es la división de documentos, como las páginas de la World Wide Web, en géneros.
Comparaciones entre agrupamientos de datos
Ha habido varias sugerencias para medir la similitud entre dos agrupamientos. Esta medida se puede utilizar para comparar el rendimiento de los diferentes algoritmos de agrupación de datos en un conjunto de datos. Muchas de estas medidas se derivan de la matriz de coincidencia (también conocida como matriz de confusión), por ejemplo, la medida Rand y las medidas Bk de Fowlkes-Mallows.
- Jain, Murty and Flynn: Data Clustering: A Review, ACM Comp. Surv., 1999. Disponible aquí.
- para otra presentación de medias k jerárquicas y medias c difusas, consulte esta introducción a la agrupación en clústeres. También tiene una explicación sobre la mezcla de Gaussianas.
- David Dowe, Página de modelado de mezclas – otros enlaces de clústeres y modelos de mezclas.
- un tutorial sobre clustering
- El libro de texto en línea: Teoría de la información, Inferencia y Algoritmos de aprendizaje, de David J.C. MacKay incluye capítulos sobre clustering de k-means, clustering de k-means suaves y derivaciones que incluyen el algoritmo E-M y la vista variacional del algoritmo E-M.
Véase también
- k
- red neuronal Artificial (ANN)
- mapa de Auto-organización
- EM (Expectation Maximization)
Bibliografía
- Clatworthy, J., Buick, D., Hankins, M., Weinman, J., & Horne, R. (2005). The use and reporting of cluster analysis in health psychology: A review (en inglés). British Journal of Health Psychology 10: 329-358.
- Romesburg, H. Clarles, Cluster Analysis for Researchers, 2004, 340 págs. ISBN 1411606175 o editorial, reimpresión de la edición de 1990 publicada por Krieger Pub. Co… Una traducción al japonés está disponible en Uchida Rokakuho Publishing Co., Ltd. Tokio, Japón.
- Heyer, L. J., Kruglyak, S. y Yooseph, S., Exploring Expression Data: Identification and Analysis of Coexpressed Genes, Genome Research 9:1106-1115.
- El libro de texto en línea: Teoría de la información, Inferencia y Algoritmos de aprendizaje, de David J.C. MacKay incluye capítulos sobre agrupamiento de k-means, agrupamiento de k-means suaves y derivaciones, incluido el algoritmo E-M y la vista variacional del algoritmo E-M.
Para agrupamiento espectral :
- Jianbo Shi y Jitendra Malik, «Normalized Cuts and Image Segmentation», IEEE Transactions on Pattern Analysis and Machine Intelligence, 22(8), 888-905, agosto de 2000. Disponible en la página web de Jitendra Malik
- Marina Meila y Jianbo Shi, «Learning Segmentation with Random Walk», Neural Information Processing Systems, NIPS, 2001. Disponible en la página de inicio de Jianbo Shi
Para estimar el número de grupos:
- Can, F., Ozkarahan, E. A. (1990) » Concepts and effectiveness of the cover coefficient-based clustering methodology for text databases.»ACM Transactions on Database Systems. 15 (4) 483-517.
Implementaciones de software
Gratuito
- el paquete flexclust para R
- YALE (Otro entorno de aprendizaje): software de código abierto gratuito para el descubrimiento de conocimientos y la minería de datos que también incluye un complemento para la agrupación en clústeres
- algunos archivos fuente Matlab para la agrupación aquí
- Paquete COMPACTO Comparativo para Evaluación de Clústeres (también en Matlab)
- mixmod : Análisis De Clústeres Y Discriminantes Basados En Modelos. Código en C++, interfaz con Matlab y Scilab
- Tutorial de clústeres de LingPipe Tutorial para realizar clústeres de enlace único y completo utilizando LingPipe, un paquete de minería de datos de texto Java distribuido con código fuente.
- Weka: Weka contiene herramientas para el procesamiento previo de datos, la clasificación, la regresión, el agrupamiento, las reglas de asociación y la visualización. También es adecuado para desarrollar nuevos esquemas de aprendizaje automático.