Dies ist eine Schritt-für-Schritt-Anleitung zum Ausführen der k-Means-Clusteranalyse in einer Excel-Tabelle von Anfang bis Ende. Bitte beachten Sie, dass auf dieser Website eine Excel-Vorlage zum kostenlosen Download zur Verfügung steht, die automatisch die Clusteranalyse ausführt. Wenn Sie jedoch wissen möchten, wie Sie ein k-Means-Clustering in Excel selbst ausführen, ist dieser Artikel genau das Richtige für Sie.
Zusätzlich zu diesem Artikel habe ich auch eine Video-Anleitung zum Ausführen der Clusteranalyse in Excel.
- Erster Schritt – Beginnen Sie mit Ihrem Datensatz
- Zweiter Schritt – Wenn nur zwei Variablen vorhanden sind, verwenden Sie ein Streudiagramm in Excel
- Schritt drei – Berechnen Sie den Abstand von jedem Datenpunkt zum Zentrum eines Clusters
- Wie funktioniert die Berechnung?
- Vierter Schritt – Berechnen Sie den Mittelwert (Durchschnitt) jedes Clustersatzes
- Schritt fünf – Wiederholen Sie Schritt 3 – der Abstand vom überarbeiteten Mittelwert
- Letzter Schritt – Diagramm und Zusammenfassung der Cluster
Erster Schritt – Beginnen Sie mit Ihrem Datensatz
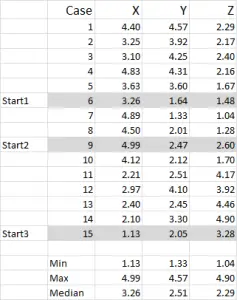
Abbildung 1
Für dieses Beispiel verwende ich 15 Fälle (oder Befragte), in denen wir die Daten für drei Variablen haben – generisch mit X, Y und Z.
Sie sollten beachten, dass die Daten in diesem Beispiel von 1 bis 5 skaliert sind. Ihre Daten können in beliebiger Form vorliegen, mit Ausnahme einer nominalen Datenskala (siehe Artikel welche Daten zu verwenden sind).
HINWEIS: Ich bevorzuge die Verwendung skalierter Daten – dies ist jedoch nicht obligatorisch. Der Grund dafür ist, Ausreißer zu „enthalten“. Angenommen, ich verwende Einkommensdaten (eine demografische Kennzahl) – die meisten Daten liegen möglicherweise zwischen 40.000 und 100.000 US–Dollar, aber ich habe eine Person mit einem Einkommen von 5 Millionen US-Dollar. Es ist für mich nur einfacher, diese Person in die Einkommensgruppe „über 250.000 US-Dollar“ einzuordnen und das Einkommen von 1 bis 9 zu skalieren – aber das liegt an Ihnen, abhängig von den Daten, mit denen Sie arbeiten.
Sie können aus diesem Beispielsatz sehen, dass drei Startpositionen hervorgehoben wurden – wir werden diese in Schritt drei unten besprechen.
Zweiter Schritt – Wenn nur zwei Variablen vorhanden sind, verwenden Sie ein Streudiagramm in Excel
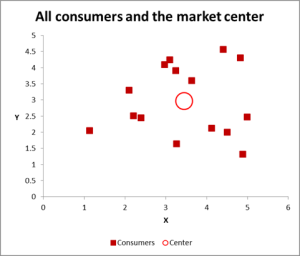
Abbildung 2
In diesem Beispiel für die Clusteranalyse verwenden wir drei Variablen – wenn Sie jedoch nur zwei Variablen zu clustern haben, ist ein Punktdiagramm eine hervorragende Möglichkeit, um zu beginnen. Und manchmal können Sie die Daten über visuelle Mittel clustern.
Wie Sie in diesem Streudiagramm sehen können, wurde jeder einzelne Fall (was ich in diesem Beispiel einen Verbraucher nenne) zusammen mit dem Durchschnitt (Mittelwert) für alle Fälle (der rote Kreis) zugeordnet.
Je nachdem, wie Sie die Daten / das Diagramm anzeigen, scheint es eine Reihe von Clustern zu geben. In diesem Fall könnten Sie drei oder vier relativ unterschiedliche Cluster identifizieren – wie in diesem nächsten Diagramm gezeigt.
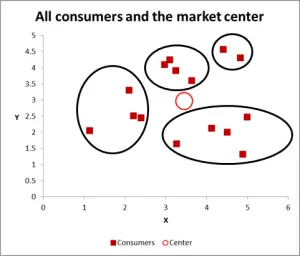
Abbildung 3
Mit diesem nächsten Diagramm habe ich wahrscheinliche Cluster sichtbar identifiziert und eingekreist. Wie ich vorgeschlagen habe, ein guter Ansatz, wenn nur zwei Variablen zu berücksichtigen sind – aber in diesem Fall haben wir drei Variablen (und Sie könnten mehr haben), so dass dieser visuelle Ansatz nur für grundlegende Datensätze funktioniert.
Schritt drei – Berechnen Sie den Abstand von jedem Datenpunkt zum Zentrum eines Clusters
Nehmen wir für dieses exemplarische Beispiel an, dass wir nur drei Segmente / Cluster identifizieren möchten. Ja, im obigen Diagramm sind vier Cluster ersichtlich, aber das betrachtet nur zwei der Variablen. Bitte beachten Sie, dass Sie mit diesem Excel–Ansatz beliebig viele Cluster identifizieren können – folgen Sie einfach demselben Konzept wie unten erläutert.
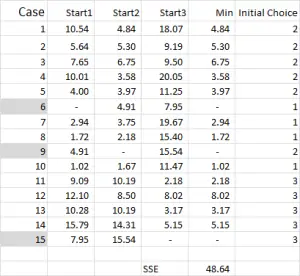
Abbildung 4
Für das k-Means-Clustering wählen Sie normalerweise einige zufällige Fälle (Startpunkte oder Seeds) aus, um die Analyse zu starten.
In diesem Beispiel – da ich drei Cluster erstellen möchte, benötige ich drei Startpunkte. Für diese Startpunkte habe ich die Fälle 6, 9 und 15 ausgewählt – aber auch beliebige zufällige Punkte könnten geeignet sein.
Der Grund, warum ich diese Fälle ausgewählt habe, ist, dass – nur bei Betrachtung der Variablen X – Fall 6 der Median, Fall 9 das Maximum und Fall 15 das Minimum war. Dies deutet darauf hin, dass diese drei Fälle etwas voneinander verschieden sind, so gute Ausgangspunkte, wie sie verteilt sind.
Bitte lesen Sie den Artikel warum Clusteranalyse manchmal zu unterschiedlichen Ergebnissen führt.
Bezogen auf die Tabellenausgabe – dies ist unsere erste Berechnung in Excel und generiert unsere „erste Auswahl“ von Clustern. Start 1 sind die Daten für Fall 6, Start 2 ist Fall 9 und Start 3 ist Fall 15. Sie sollten beachten, dass der Schnittpunkt von jedem von ihnen eine 0 (-) in der Tabelle ergibt.
Wie funktioniert die Berechnung?
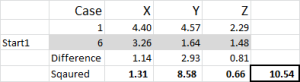
Abbildung 5
Schauen wir uns die erste Zahl in der Tabelle an – Fall 1, Start 1 = 10,54.
Denken Sie daran, dass wir Fall 6 willkürlich als zufälligen Startpunkt für Cluster 1 festgelegt haben. Wir wollen die Entfernung berechnen und verwenden die Quadratsummenmethode – wie hier gezeigt. Wir berechnen die Differenz zwischen jedem der drei Datenpunkte in der Menge, quadrieren dann die Differenzen und summieren sie dann.
Wir können es „mechanisch“ tun, wie hier gezeigt – aber Excel hat eine eingebaute Formel zu verwenden: SUMXMY2 – das ist viel effizienter zu bedienen.
Unter Bezugnahme auf Abbildung 4 ermitteln wir dann den Mindestabstand für jeden Fall von jedem der drei Startpunkte – dies sagt uns, zu welchem Cluster (1, 2 oder 3) der Fall am nächsten liegt –, der in der Spalte ‚Initial Choice‘ angezeigt wird.
Vierter Schritt – Berechnen Sie den Mittelwert (Durchschnitt) jedes Clustersatzes
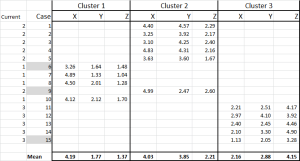
Abbildung 6
Wir haben nun jeden Fall seinem ursprünglichen Cluster zugewiesen – und wir können das mit einer IF-Anweisung in einer Tabelle auslegen (wie in Abbildung 6 gezeigt).
Am Ende der Tabelle haben wir den Mittelwert (Durchschnitt) jedes dieser Fälle. N0w – anstatt sich auf nur einen „repräsentativen“ Datenpunkt zu verlassen – haben wir eine Reihe von Fällen, die jeden repräsentieren.
Schritt fünf – Wiederholen Sie Schritt 3 – der Abstand vom überarbeiteten Mittelwert
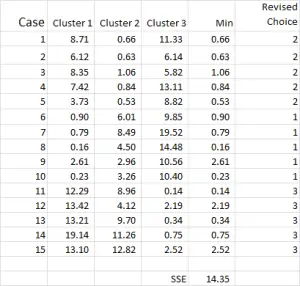
Abbildung 7
Der Clusteranalyseprozess besteht nun darin, die Schritte 4 und 5 (Iterationen) zu wiederholen, bis sich die Cluster stabilisieren.
Jedes Mal verwenden wir den überarbeiteten Mittelwert für jeden Cluster. Daher zeigt Abbildung 7 unsere zweite Iteration – diesmal verwenden wir jedoch die Mittelwerte, die am Ende von Abbildung 6 generiert wurden (anstelle der Startpunkte aus Abbildung 1).
Sie können jetzt sehen, dass es eine geringfügige Änderung in der Clusteranwendung gegeben hat, wobei Fall 9 – einer unserer Ausgangspunkte – neu zugewiesen wurde.
Sie können auch die unten berechnete Summe des quadratischen Fehlers (SSE) sehen – die Summe der einzelnen Mindestabstände. Unser Ziel ist es nun, die Schritte 4 und 5 zu wiederholen, bis die SSE nur eine minimale Verbesserung zeigt und / oder die Clusterzuordnungsänderungen bei jeder Iteration geringfügig sind.
Letzter Schritt – Diagramm und Zusammenfassung der Cluster
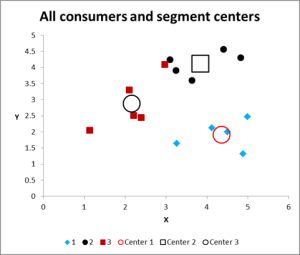
Abbildung 8
Nachdem wir mehrere Iterationen ausgeführt haben, haben wir jetzt die Ausgabe, um die Daten grafisch darzustellen und zusammenzufassen.
Hier ist das Ausgabediagramm für dieses Excel-Beispiel für die Clusteranalyse.
Wie Sie sehen können, werden drei verschiedene Cluster angezeigt, zusammen mit den Schwerpunkten (Durchschnitt) jedes Clusters – den größeren Symbolen.
Diese Daten können wir bei Bedarf auch tabellarisch darstellen, wie wir es in Excel ausgearbeitet haben.
Bitte schauen Sie sich den Fall in Cluster 3 an – das kleine rote Quadrat direkt neben dem schwarzen Punkt in der oberen Mitte des Diagramms. Dieser Fall sitzt dort wegen des Einflusses der dritten Variablen, die in diesem Diagramm mit zwei Variablen nicht dargestellt ist.