Terminologie:
- IDS = Strom von Drain zu Source ODER Drain-Source-Strom
- VDS = Drain zu Source-Spannung
- L = Länge des Kanals
Im Idealfall wird IDS im Sättigungsbereich unabhängig von VDS, d.h. im Sättigungsbereich wird der Kanal am Drain-Ende abgeklemmt und eine weitere Erhöhung von VDS hat keinen Einfluss auf die Kanalform.
In der Praxis wirkt sich die Erhöhung des VDS jedoch auf den Kanal aus. Im Sättigungsbereich, wenn VDS zunimmt, Der Kanalabklemmpunkt wird leicht vom Drain wegbewegt, in Richtung der Quelle, wenn das Drainelektronenfeld es zurück „drückt“. Der Sperrvorspannungsverarmungsbereich erweitert sich und die effektive Kanallänge nimmt um einen Betrag von ∆L für eine Erhöhung von VDS ab.
Somit „berührt“der Kanal den Abfluss nicht mehr und erhält eine asymmetrische Form, die am Abflussende dünner ist. Dieses Phänomen wird als Kanallängenmodulation bezeichnet.
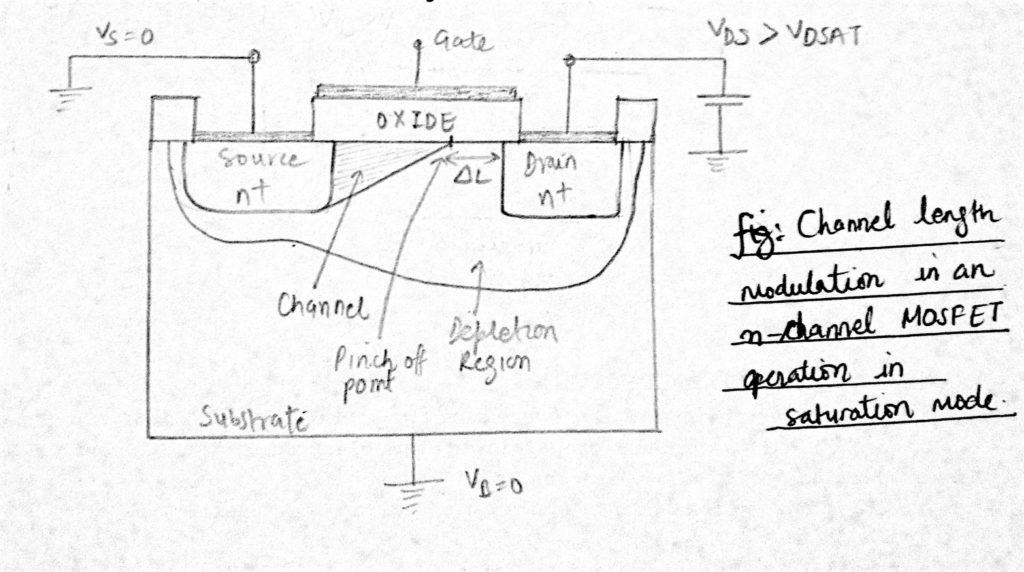
Bei großen Geräten ist dieser Effekt vernachlässigbar, aber für kürzere Geräte wird ∆L/L wichtig. Auch im Sättigungsbereich aufgrund der Kanallängenmodulation nimmt IDS mit zunehmender VDS zu und nimmt auch mit abnehmender Kanallänge L zu.
Die Spannungs-Strom-Kurve ist in diesem Bereich nicht mehr flach.
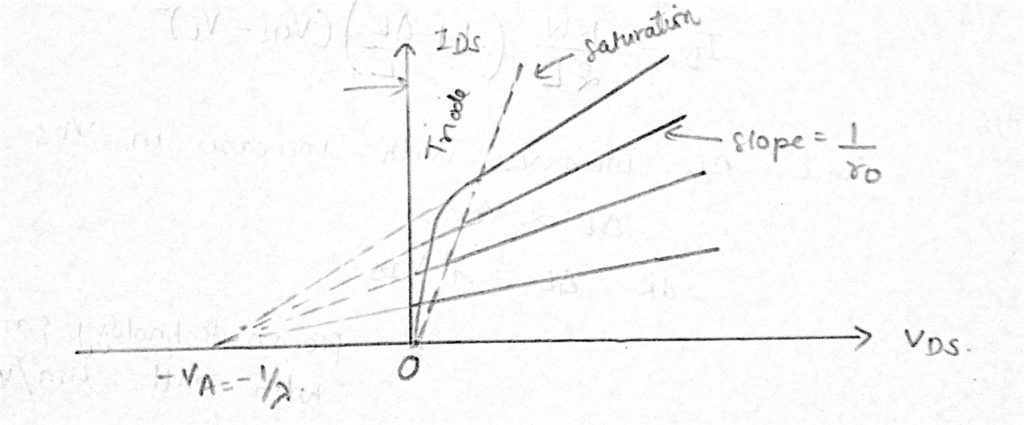
Der Drainstrom bei Kanallängenmodulation ist gegeben durch:
ABLEITUNG:
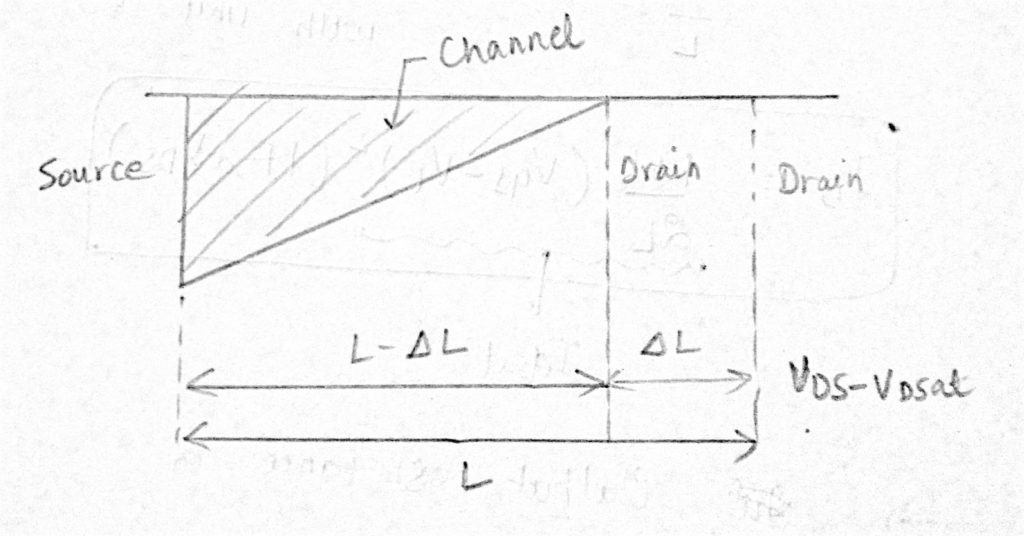
Um die Abhängigkeit von ID von VDS im Sättigungsbereich zu berücksichtigen, ersetzen Sie L durch L – ∆L. Wir wissen, dass im Sättigungsbereich der Drain-Source-Strom (IDS = ID) gegeben ist durch:
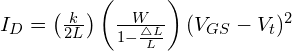
Angenommen 
Da ∆L mit zunehmendem VDS zunimmt
ODER
wobei 
= prozesstechnischer Parameter mit Einheit µm/V.
daher,
wo,
= prozesstechnischer Parameter mit Einheit V-1
